文章目录
- 前言
- 并查集原理
- 并查集的模拟实现
- leetcode练习
- 省份数量
- 等式方程的可满足性
前言
并查集通常会作为高阶数据结构的一个子结构使用,虽然原理不是很难,但其思想值得我们好好学习
并查集原理
并查集是一种树形结构,其保存了多个集合,每个集合以树的形式体现,所以说并查集是一片森林。不像二叉树有着严格的节点限制,并查集的树可以有任意棵子树,这也导致了在使用并查集处理海量数据时需要设计路径压缩算法,以提高查找元素的效率。当然这是后话了,并查集用来做什么呢?其最主要的应用是判断两个元素是否在同一集合(同一棵树)中,由此衍生了其他应用:查找一个元素所在的集合,将两个不同集合的元素合并从而使两个集合合并为一个集合,以及并查集中的集合个数。
那么并查集通过什么表示元素之间的关系呢?和优先级队列(大小堆)相似,优先级队列用数组下标表示节点之间的关系,元素存储在数组中。并查集相反,元素被抽象成数组下标,数组中存储的值表示元素间的关系,通常这个数组存储int,并初始化为-1,数组用整数来表示元素之间的关系。这里画图讲解
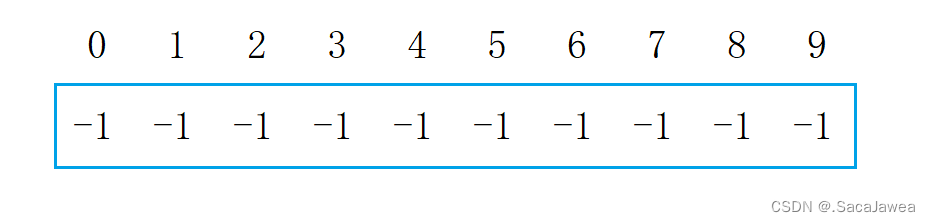
虽然并查集是树形结构,但是它与优先级队列一样,逻辑上是树形结构,物理上确是一个连续的数组。从上图中可以看出,数组有10个元素(这里为了讲解方便,假设元素的值与数组下标相同),每个元素在并查集中的值都是-1,这表示每个元素自成一个集合,互相之间没有联系。现在将3和4合并到一个集合,假设3是集合中的根,我们要做的是把4在并查集中的值加到3在并查集中的值上,修改为-2。接着将4在并查集中的值修改为3在并查集中的下标,由于3在并查集中的下标就是3,所以把4在并查集中的值修改为3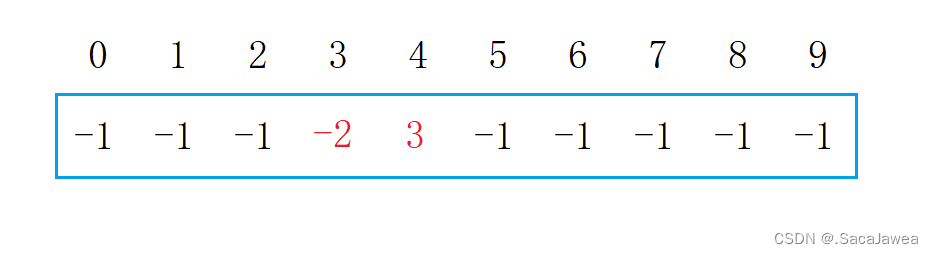
这也就能解释为什么要把并查集中的值初始化为-1了,3和4现在处于一个集合中,3作为集合的根,它在并查集中的值是-2,绝对值为2表示这个集合中有2个元素,而4在并查集中的值为3,这个值就是3在并查集中的下标。所以总结一下,负数表示该元素是一个集合的根,其绝对值就是该集合中的元素个数。一开始元素之间互相没有联系,所以它们的值是-1,说明它们自成一个集合并作为集合的根。当一个元素在并查集中的值是一个正数,说明该元素处于一个集合中,且该元素在并查集中的值就是其双亲元素在并查集中的下标。4在并查集中的值是3,说明4处于一个集合中,其双亲节点在并查集中的下标是3
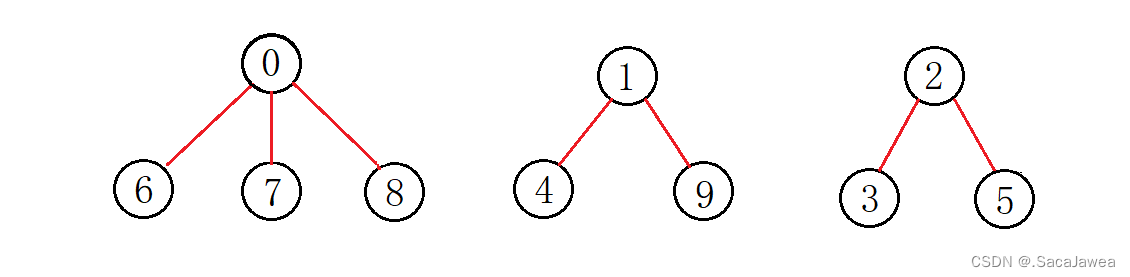
假设现在元素之间的关系如上图所示,那么并查集会是怎样的?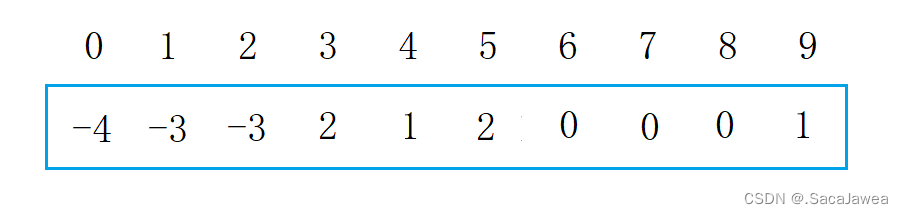
现在并查集中有三个集合,它们的根分别是0,1,2,所以0,1,2在并查集中的值都是负数,它们的子元素在并查集中的值为它们在并查集中的下标。理解了并查集中元素之间的映射关系,现在就可以讲解并查集的算法了。第一个算法是合并两个元素,其本质是两个集合之间的合并,使两个集合的元素都联系起来,比如我要把8和4合并,由于8和4都是集合的子元素,所以我们要先找到集合的根元素,根据元素在并查集中的值为正数,说明它是集合中的子元素,并且该值是其双亲元素在并查集中的下标,所以我们可以在并查集中找到它的双亲元素,如果该元素在并查集中的值为负数,该元素就是集合的根元素。这就是查找一个元素所在集合的算法逻辑,根据这个逻辑找到两个子元素的根元素,再判断哪个集合的元素多,将元素少的集合合并到元素多的集合中。8所在的集合有4个元素,比4所在集合的元素个数多,所以将4所在集合合并到8所在集合中。此时我们只要把4所在集合的根元素,1作为8所在集合的根元素的子元素即可:把1在并查集中的值加到0在并查集中的值上,然后把1在并查集中的值修改为0在并查集中的下标——0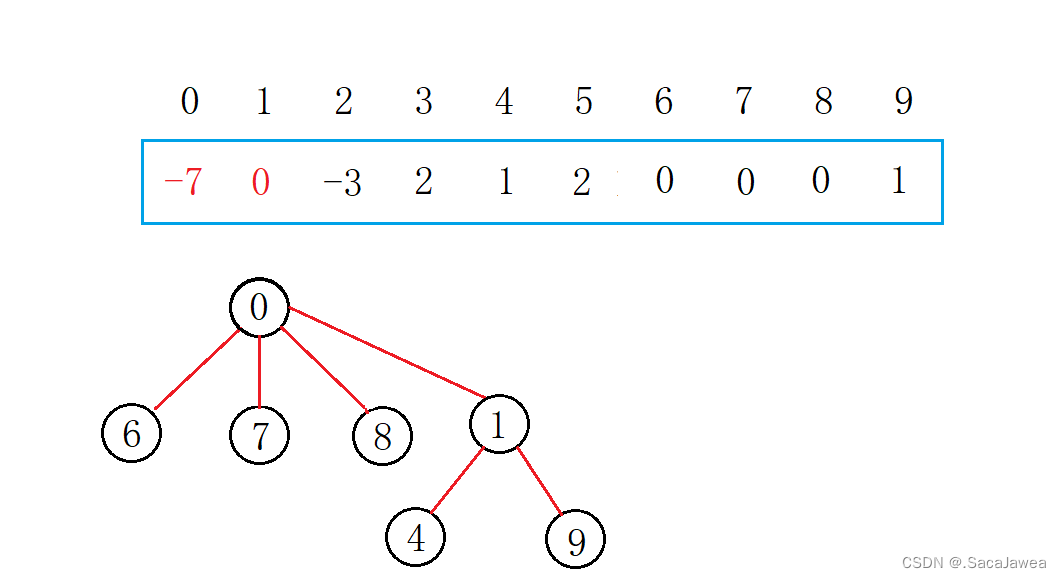
这就是合并算法的逻辑,至于判断两个元素是否在同一集合中,只要分别查找两个元素的根元素,判断根元素是否相等即可,查找根元素的逻辑刚才也说过了。至此并查集的算法也大概讲解完了,接下来是其模拟实现
并查集的模拟实现
可以注意到,我在讲解算法时不厌其烦的提到某元素在并查集中的值,而不是直接说某元素的值呢?讲解算法之前我做了一个假设,元素的值与数组下标的值相等,就是说并查集存储的元素是一些整数。但并查集可不是一定只能存储整数的,它还可能存储字符串,一些自定义类型,那么这些类型与整数之间没有直接的关系,我们就要将它们抽象成整数。比如要判断两个字符串是否在一个集合中,我们要做的是先将它们转换成整数,将这个整数作为数组下标,根据该位置的值进行后续的判断。而刚才我的讲解没有映射的过程,或者说是直接映射,元素与数组下标的值相等,对此就不需要做转换。但是,针对泛型,我们需要保存其与整数之间的映射关系,可以使用unordered_map保存,将泛型T与int整数作为pair对象,存储进unordered_map中,使用者传入泛型对象,我们需要将其转换成int对象再进行相关的计算
template <class T>
class UnionFindSet
{
public:
UnionFindSet(const T* arr, size_t n) // 用一个泛型数组初始化,并指定元素个数n
{
for (size_t i = 0; i < n; ++i)
{
add_elm(arr[i]); // 接口的复用
}
}
// 添加元素到并查集中
void add_elm(const T& data)
{
// typename unordered_map<T, int>::iterator ret = _to_int.find(arr[i]);
auto ret = _to_int.find(data);
if (ret == _to_int.end()) // 并查集中没有这个元素才可以存储
{
_to_int[data] = _ufs.size(); // 将泛型与数组下标之间建立映射
_ufs.push_back(-1);
}
}
private:
vector<int> _ufs; // 保存元素之间关系的数组
unordered_map<T, int> _to_int; // 保存泛型与整数之间的转换的哈希桶
};
先定义出构造函数与添加元素的接口,注意并查集需要去重,如果不去重,元素与整数之间的转换就具有了歧义
template <class T>
class UnionFindSet
{
public:
UnionFindSet(const T* arr, size_t n) // 用一个泛型数组初始化,并指定元素个数n
{
for (size_t i = 0; i < n; ++i)
{
add_elm(arr[i]); // 接口的复用
}
}
UnionFindSet() = default;
// 添加元素到并查集中
void add_elm(const T& data)
{
// typename unordered_map<T, int>::iterator ret = _to_int.find(arr[i]);
auto ret = _to_int.find(data);
if (ret == _to_int.end()) // 并查集中没有这个元素才可以存储
{
_to_int[data] = _ufs.size(); // 将泛型与数组下标之间建立映射
_ufs.push_back(-1);
}
}
size_t find_root(size_t index) // 查找index下标的根元素,返回其下标
{
size_t root = index;
while (_ufs[root] >= 0) // 根元素在并查集中的值是负数
{
root = _ufs[root];
}
while (_ufs[index] >= 0)
{
size_t parent = _ufs[index]; // 先保存其双亲,以对其双亲也进行路径压缩
_ufs[index] = root; // 路径压缩
index = parent;
}
return root;
}
// 判断一个元素是否存在于并查集中,如果是返回其下标,否则返回-1
size_t in_test(const T& data)
{
auto it = _to_int.find(data);
if (it == _to_int.end()) // 如果元素不存在
{
return -1;
}
return it->second;
}
bool set_test(const T& data1, const T& data2) // 判断两个元素是否在同一集合中
{
size_t index1 = in_test(data1);
size_t index2 = in_test(data2);
if (index1 == -1 || index2 == -1) // 如果有一个元素不存在,抛异常
{
throw invalid_argument("set_test()::元素不存在");
}
return find_root(index1) == find_root(index2); // 返回两元素的根元素下标是否相等
}
// 连接两个集合
void set_union(const T& data1, const T& data2)
{
size_t index1 = in_test(data1);
size_t index2 = in_test(data2);
if (index1 == -1 || index2 == -1) // 如果有一个元素不存在,抛异常
{
throw invalid_argument("union()::元素不存在");
}
// 找到它们的根元素下标
size_t root1 = find_root(index1);
size_t root2 = find_root(index2);
if (root1 != root2) // 不同集合才能合并
{
// 假设root1为根元素的集合元素个数更多,如果它的元素更少,交换
// 注意根元素在并查集中存储的是负数
if (_ufs[root1] > _ufs[root2])
{
swap(root1, root2);
}
_ufs[root1] += _ufs[root2]; // 数值的累加,维护集合的个数
_ufs[root2] = root1; // 将小集合作为大集合的子集,保存大集合根元素的下标
}
}
size_t set_size() // 返回并查集中树的个数
{
// 遍历数组,只有有值小于0就说明它是一个根元素,树的个数加1
size_t ret = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
{
ret++;
}
}
return ret;
}
// for test
void print()
{
for (size_t i = 0; i < _ufs.size(); ++i)
{
cout << _ufs[i] << ' ';
}
cout << endl;
}
private:
vector<int> _ufs; // 保存元素之间关系的数组
unordered_map<T, int> _to_int; // 保存泛型与整数之间的转换的哈希桶
};
最后是所有接口的实现,由于前面已经讲过了逻辑,并且代码带有详细的注释,这里就不再赘述了。需要注意的是合并集合时需要先判断,只有不同集合才能合并,然后是需要将小集合合并到大集合中,如果反过来可能会出现某一路径过长的问题。除此之外,在查找一个元素的根节点时,可以强制的进行路径压缩,将该元素到其根元素之间的所有元素作为根的最近子元素,以提高查找根元素的效率
最后是demo的测试
int main()
{
int arr[] = { 0,1,2,3,4,5,6,7,8,9 };
UnionFindSet<int> uset(arr, 10);
uset.set_union(0, 6);
uset.set_union(6, 7);
uset.set_union(7, 8);
uset.set_union(1, 4);
uset.set_union(4, 9);
uset.set_union(2, 3);
uset.set_union(3, 5);
cout << uset.set_test(3, 5) << endl;
cout << uset.set_test(1, 5) << endl << endl;
cout << uset.set_size() << endl << endl;
uset.print();
}
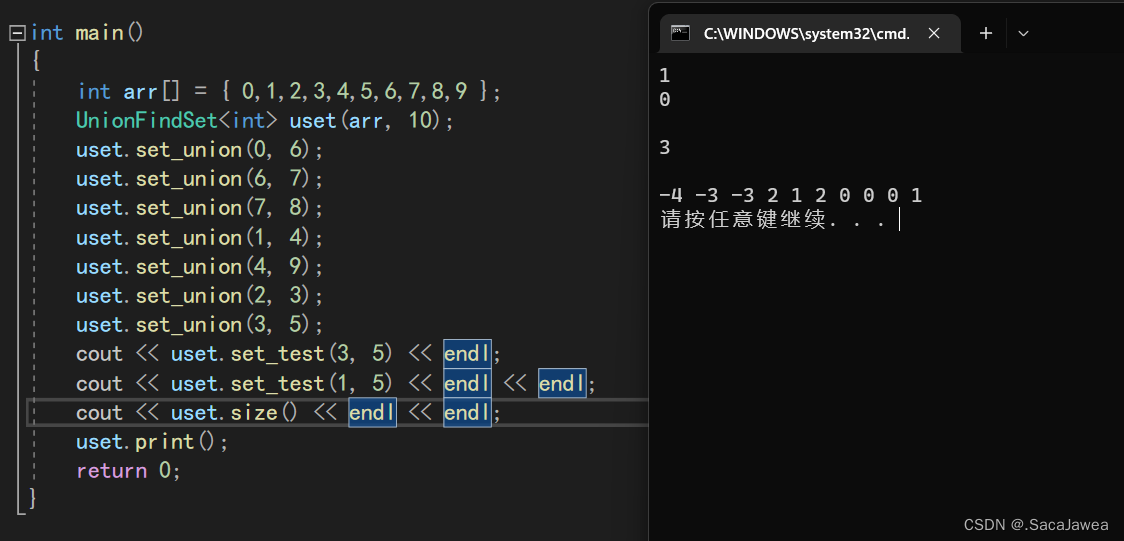
测试的数据与之前讲解算法逻辑时用到的例子一样,经过大概的测试,模拟实现的并查集没有严重的bug
leetcode练习
省份数量
题目链接

首先,每个测试样例会给出一个n*n的二维矩阵,表示每个城市之间是否相连,并且一组相连的城市就是一个省份,问给定的二维数组中有几个省份?这不就是并查集中的树的数量吗?城市就是并查集中的元素,我们只要遍历二维数组,将相连的城市放到一个集合中,最后返回并查集中的树的数量即可
题目没有给出具体的城市名称,而是给出抽象的数字,用数组下标表示一个城市,所以并查集存储int就行了。首先,调用默认构造创建一个并查集,再调用add_ele接口初始化并查集,接着遍历二维数组调用set_union接口连接相连的城市,最后返回并查集中树的数量
int findCircleNum(vector<vector<int>>& isConnected) {
UnionFindSet<int> uset;
for (size_t i = 0; i < isConnected.size(); ++i)
{
uset.add_elm(i);
}
for (size_t i = 0; i < isConnected.size(); ++i)
{
for (size_t j = 0; j < isConnected[i].size(); ++j)
{
if (isConnected[i][j] == 1)
{
uset.set_union(i, j);
}
}
}
return uset.set_size();
}
上面这种解法需要现场搓一个并查集出来,但是只要掌握并查集的思想我们也能解出这道题,不用手搓一个并查集。由于题目直接用数字表示城市,所以我们可以不需要创建保存元素与整数之间映射关系的unordered_map,只用一个vector数组,数组的下标与城市是直接映射的关系。将vector数组resize(n)并给定初始值-1,然后写一个合并集合的lambda,遍历二维数组连接相连的城市,最后遍历我们创建的数组,有几个负数就有几个省份
int findCircleNum(vector<vector<int>>& isConnected) {
vector<int> ufs(isConnected.size(), -1); // 并查集数组
auto find_root = [&](size_t pos) {
while (ufs[pos] >= 0)
{
pos = ufs[pos];
}
return pos;
};
auto set_union = [&](size_t pos1, size_t pos2) {
size_t root1 = find_root(pos1);
size_t root2 = find_root(pos2);
if (root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
};
for (size_t i = 0; i < isConnected.size(); ++i)
{
for (size_t j = 0; j < isConnected[i].size(); ++j)
{
// 相连的城市放到同一集合中
if (isConnected[i][j] == 1)
{
set_union(i, j);
}
}
}
// 树(省份)的统计
size_t ret = 0;
for (auto& v : ufs)
{
if (v < 0)
{
ret++;
}
}
return ret;
}
等式方程的可满足性
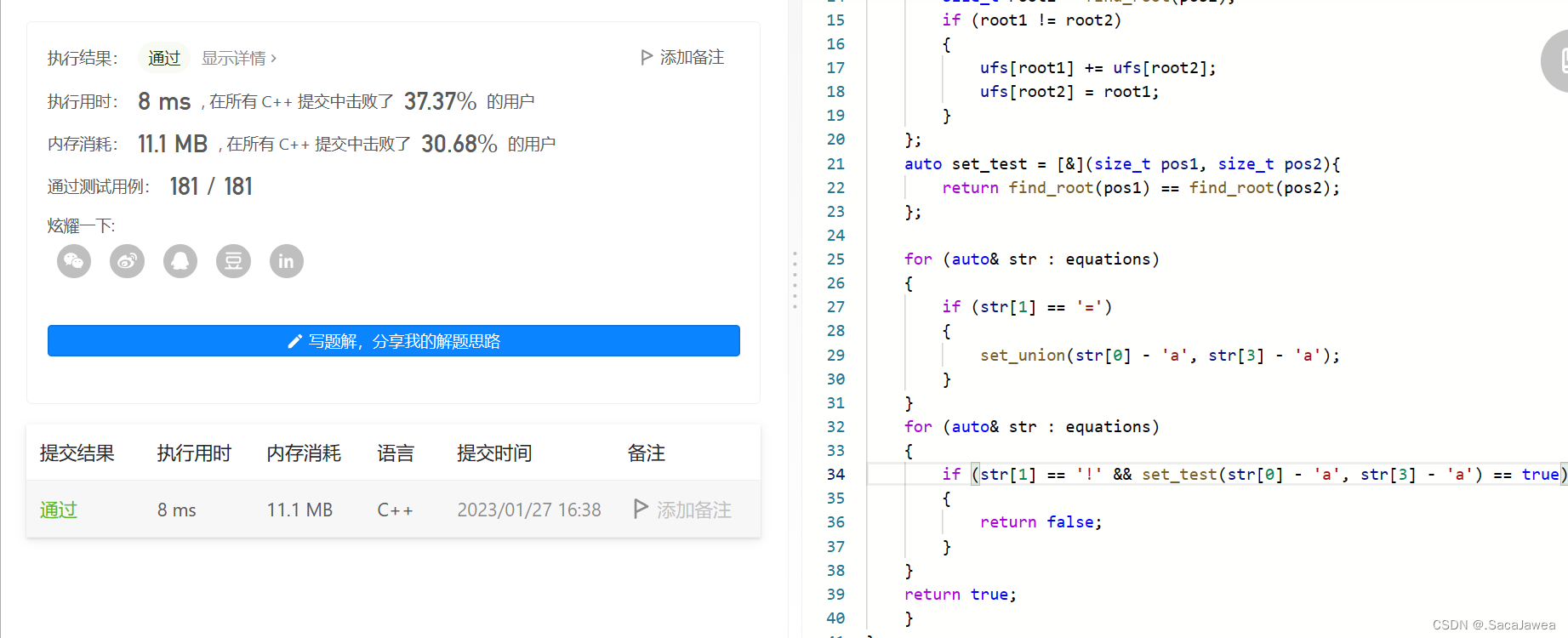
这道题就是判断给定的字符串是否有自相矛盾的问题,我们先遍历一遍,把数值相等的字母放在一个集合中,然后再遍历一遍,判断不相等的字母有没有在同一集合中,如果有就说明示例矛盾,返回false。没啥好说的,这题只是多了一个是否处于同一集合的判断
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
vector<int> ufs(26, -1); // 直接映射26个小写字母
auto find_root = [&](size_t pos) {
while (ufs[pos] >= 0)
{
pos = ufs[pos];
}
return pos;
};
auto set_union = [&](size_t pos1, size_t pos2) {
size_t root1 = find_root(pos1);
size_t root2 = find_root(pos2);
if (root1 != root2)
{
ufs[root1] += ufs[root2];
ufs[root2] = root1;
}
};
auto set_test = [&](size_t pos1, size_t pos2){
return find_root(pos1) == find_root(pos2);
};
for (auto& str : equations)
{
if (str[1] == '=')
{
// 相等字母放入同一集合中
set_union(str[0] - 'a', str[3] - 'a');
}
}
for (auto& str : equations)
{
// 判断不相等的字母是否在同一集合中,如果是,返回false
if (str[1] == '!' && set_test(str[0] - 'a', str[3] - 'a') == true)
{
return false;
}
}
return true;
}
};