💡 本次解读的文章是 2019 年发表于 SIGIR 的一篇基于图卷积神经网络的用户物品协同过滤推荐算法论文， 论文将用户-物品交互信息建模为二分图，提出了一个基于二分图的推荐框架 Neural Graph Collaborative Filtering（NGCF），有效地将协作信号以显式的方式注入到嵌入过程中，并利用 GNN 捕捉高阶交互信息，以此提高预测的效果。

一、本文贡献

（1）说明了在基于模型 CF 方法的嵌入中显式地利用协作信号的重要性；

（2）提出了一种高阶、显式编码协助信号的图神经网络推荐框架 NGCF；

（3）在 300 万规模的数据集上进行了实证研究，结果证明了 NGCF 的有效性。

二、NGCF 框架

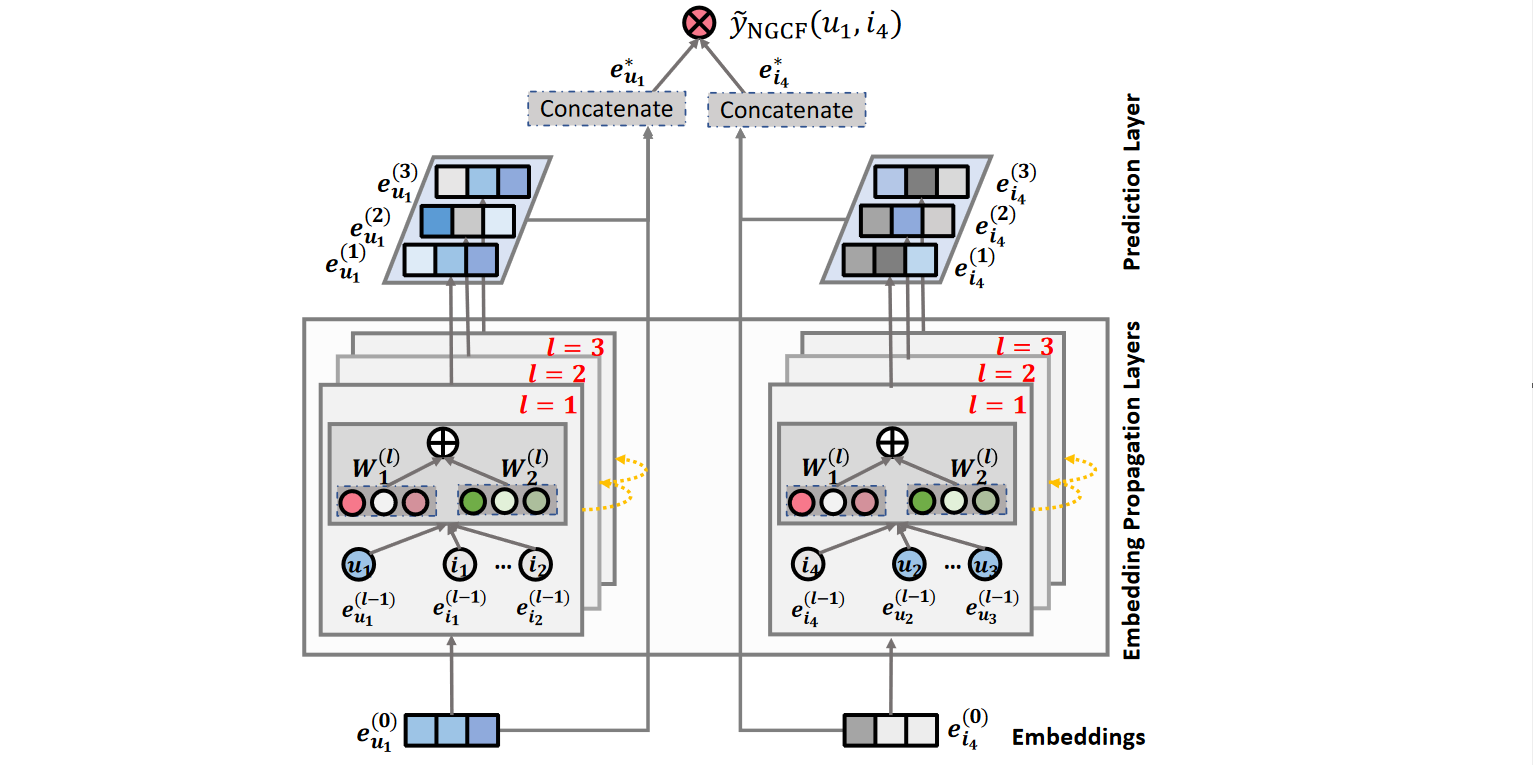
NGCF 框架主要有三个部分组成，分别是嵌入层（Embeddings Layer）、嵌入传播层（Embedding Propagation Layers）以及预测层（Prediction Layer）。

2.1 嵌入层

对于一个用户 $u$ （或物品 $i$），首先利用 one-hot 编码进行向量表示，再利用 embedding 技术获取大小为 $d$ 的嵌入表示 ${\mathbf{e}}_u\in {\mathbb{R}}^d({\mathbf{e}}_i\in {\mathbb{R}}^d)$，以此构建出一个作为嵌入查找表的参数矩阵：

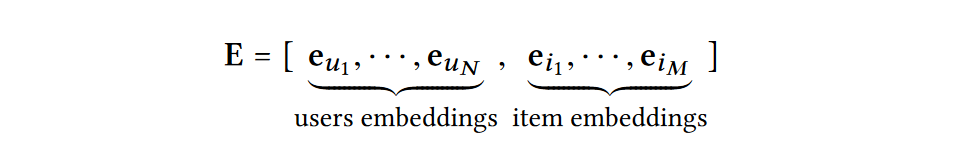
将上述嵌入表作为用户嵌入和物品嵌入的初始状态，并通过后续的图神经网络以端到端方式进行优化，增强嵌入表示中的协同信号。

2.2 嵌入传播层

嵌入传播过程的介绍主要分为一阶传播和高阶传播两个部分。

（1）一阶传播

从直观上看，与用户发生过交互的物品一定程度上反映了用户的偏好，依据协同过滤的思想，与某一物品发生过交互行为的用户可以作为该物品的特征，进一步地，基于此特征衡量两个物品的协同相似度。而这一过程主要通过一阶传播实现，该过程包含两个主要操作：消息构建和消息聚合。

• 消息构建

对于存在交互行为的用户-物品对 $(u,i)$，将从物品 $i$ 流向用户 $u$ 的消息定义为：

$${\mathbf{m}}_{u\leftarrow i}=f\left({\mathbf{e}}_i,{\mathbf{e}}_u,p_{ui}\right)$$
其中，${\mathbf{m}}_{u\leftarrow i}$ 为传播消息的嵌入表示，$f(\cdot )$ 是消息编码函数，它以嵌入 ${\mathbf{e}}_i$ 和 ${\mathbf{e}}_u$ 作为输入，利用系数$p_{ui}$控制边 $(u,i)$ 上每次传播的衰减因子。在本文中上述消息定义的具体实现为：
$${\mathbf{m}}_{u\leftarrow i}=\frac{1}{\sqrt{\left|{\mathcal{N}}_u\Vert {\mathcal{N}}_i\right|}}\left({\mathbf{W}}_1{\mathbf{e}}_i+{\mathbf{W}}_2\left({\mathbf{e}}_i\odot {\mathbf{e}}_u\right)\right)$$
其中，${\mathbf{W}}_1,{\mathbf{W}}_1\in {\mathbb{R}}_{d^{\prime }\times d}$ 是可训练的权重矩阵，用于提取传播中的有用信息，$d^{\prime }$ 表示变换大小，$\odot$ 表示逐位乘积，${\mathbf{e}}_i\odot {\mathbf{e}}_u$ 表示物品与用户交互信息的编码。这里用图拉普拉斯范数 $\frac{1}{\sqrt{|{\mathcal{N}}_u\Vert {\mathcal{N}}_i|}}$ 作为 $p_{ui}$ 的取值，${\mathcal{N}}_u$ 和 ${\mathcal{N}}_i$ 分别表示用户 $u$ 和物品 $i$ 的一跳邻居，其反映了历史物品对用户偏好的贡献程度，且传播的消息随路径长度衰减。

• 消息聚合

在获取了消息的表示后，对于用户 $u$ 需要对邻域传播来的消息进行聚合，以此更新 $u$ 的嵌入表示。具体地，将聚合函数定义为：
$${\mathbf{e}}_u^{(1)}=LeakyReLU({\mathbf{m}}_{u\leftarrow u}+\sum _{i\in {\mathcal{N}}_i}{\mathbf{m}}_{u\leftarrow i})$$
其中，${\mathbf{e}}_u^{(1)}$ 表示经过第一个嵌入传播层后得到的用户 $u$ 嵌入表示，${\mathbf{m}}_{u\leftarrow u}$ 表示用户的自连接，它保留了原始特征的信息。类似地，可以通过从物品 $i$ 连接的用户传播信息来获得物品 $i$ 的嵌入表示 ${\mathbf{e}}_i^{(1)}$。

（2）高阶传播

在获取了一阶传播表示后，可以通过堆叠更多的图神经网络层，来获取高阶交互信息。通过堆叠 $l$ 个嵌入传播层，用户和物品能够接收从其 $l$ 跳邻居传播的消息，在第 $l$ 步中，用户 $u$ 的嵌入表示为：
$${\mathbf{e}}_u^{(l)}=LeakyReLU({\mathbf{m}}_{u\leftarrow u}^{(l)}+\sum _{i\in {\mathcal{N}}_i}{\mathbf{m}}_{u\leftarrow i}^{(l)})$$
其中，${\mathbf{m}}_{u\leftarrow i}^{(l)}=p_{ui}({\mathbf{W}}_1^{(l)}{\mathbf{e}}_i^{(l-1)}+{\mathbf{W}}_2^{(l)}({\mathbf{e}}_i^{(l-1)}\odot {\mathbf{e}}_u^{(l-1)}))$，${\mathbf{m}}_{u\leftarrow u}^{(l)}={\mathbf{W}}_1^{(l)}{\mathbf{e}}_u^{(l-1)}$，${\mathbf{W}}_1,{\mathbf{W}}_2\in {\mathbb{R}}^{d_l\times d_{l-1}}$ 表示可训练的变换矩阵。

（3）矩阵表示

基于上述一阶传播和高阶传播的向量化表示，将传播过程以矩阵的形式进行统一表示：
$${\mathbf{E}}^{(l)}=\mathrm{LeakyReLU}\left((\mathcal{L}+\mathbf{I}){\mathbf{E}}^{(l-1)}{\mathbf{W}}_1^{(l)}+\mathcal{L}{\mathbf{E}}^{(l-1)}\odot {\mathbf{E}}^{(l-1)}{\mathbf{W}}_2^{(l)}\right)$$
其中，${\mathbf{E}}^{(l)}\in {\mathbb{R}}^{(N+M)\times d_l}$ 是经过 $l$ 步嵌入传播后得到的用户和物品的表示，${\mathbf{E}}^{(0)}$ 表示初始嵌入，即 ${\mathbf{e}}_u^{(0)}={\mathbf{e}}_u,{\mathbf{e}}_i^{(0)}={\mathbf{e}}_i$，$\mathbf{I}$ 表示单位矩阵，$\mathcal{L}$ 表示用户-物品二分图的拉普拉斯矩阵：
$$\mathcal{L}={\mathrm{D}}^{-\frac{1}{2}}{\mathrm{AD}}^{-\frac{1}{2}}\text{ and }\mathrm{A}=\left[\begin{array}{cc}0& \mathbf{R}\\ {\mathbf{R}}^{\top }& 0\end{array}\right]$$
其中，$\mathbf{R}\in R^{N\times M}$ 表示用户-物品交互矩阵，$\mathbf{A}$ 为邻接矩阵，$\mathbf{D}$ 为对角度矩阵（第 $t$ 个对角元素 $D_{tt}=|N_t|$，因此，有 ${\mathcal{L}}_{ui}=1/\sqrt{\left|{\mathcal{N}}_u\right|\left|{\mathcal{N}}_i\right|}$。这种通过矩阵表示的传播规则，可以丢弃节点采样过程，以相当高效的方式同时更新所有用户和物品的表示，这意味着该方法可以在大规模图上运行。

2.3 预测层

在经过 $L$ 层嵌入传播层后，可以得到用户 $u$ 的多个嵌入表示 $\left\{{\mathbf{e}}_u^{(1)},\cdots ,{\mathbf{e}}_u^{(L)}\right\}$，由于不同层得到的表示强调的是通过不同连接传递的消息，它们在反映用户偏好方面的贡献不同。因此，这里主要利用拼接操作，将它们拼接成最终的嵌入表示：
$${\mathbf{e}}_u^{\ast }={\mathbf{e}}_u^{(0)}\Vert \cdots \Vert {\mathbf{e}}_u^{(L)},{\mathbf{e}}_i^{\ast }={\mathbf{e}}_i^{(0)}\Vert \cdots \Vert {\mathbf{e}}_i^{(L)}$$
在分别获取了用户 $u$ 和物品 $i$ 的最终嵌入表示后，可以利用内积来估计用户对目标物品的偏好：

$${\hat{y}}_{\mathrm{NGCF}}(u,i)={\mathbf{e}}_u^{\ast \top }{\mathbf{e}}_i^{\ast }$$

三、模型训练

（1）损失函数定义

为了学习模型参数，论文使用了成对 BPR 损失函数，它考虑了观察到的和未观察到的用户-物品交互之间的相对顺序，即 BPR 假设观察到的交互比未观察到的交互更能反映用户的偏好，应该赋予更高的预测值，目标函数如下：
$$\text{ Loss }=\sum _{(u,i,j)\in O}-\ln \sigma \left({\hat{y}}_{ui}-{\hat{y}}_{uj}\right)+\lambda \Vert \Theta {\Vert }_2^2$$
其中， O = { ( u , i , j ) ∣ ( u , i ) ∈ R + , ( u , j ) ∈ R − } O=\left\{(u, i, j) \mid(u, i) \in \mathcal{R}^{+},(u, j) \in \mathcal{R}^{-}\right\} O={(u,i,j)∣(u,i)∈R+,(u,j)∈R−}，训练集中的数据对，${\mathcal{R}}^{+}$ 表示观察到的交互，${\mathcal{R}}^{-}$ 表示未观察到的交互，$\sigma (\cdot )$ 表示 sigmoid 函数，$\Theta =\left\{\mathbf{E},{\left\{{\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}\right\}}_{l=1}^L\right\}$，$\lambda$ 用于控制 L2 正则化强度，防止过拟合。这里论文采用 mini-batch Adam 优化预测模型并更新模型参数，对于一批随机采样的三元组 $(u,i,j)\in O$，在传播 $L$ 步后建立其表示为 $[e^{(0)},\cdots ,e^{(L)}]$，然后利用损失函数的梯度更新模型参数。

（2）消息和节点的 Dropout

Dropout 操作主要用于缓解模型的过拟合现象，一般只在训练中使用，在测试时禁用。本文的方法在训练时，以概率 $p1$ 删除传播过程中的消息，即在第 $l$ 个传播层中，只有部分消息贡献于嵌入表示。另外，本文的方法还进行了节点丢弃来随机阻塞特定的节点并丢弃其所有的传出消息，即对于第 $l$ 个传播层，随机丢弃拉普拉斯矩阵的 $(M+N)p2$ 个节点，其中 $p2$ 为丢弃率。