一、通俗理解状态机DP

其实状态机DP只是听起来高级，其实我们之前做的所有关于DP的题几乎都算是状态机，为什么呢？

1、什么是状态机

大家继续向下看：

DP解决的是多决策的问题，那么我们可以把01背包问题画成下面的图：
按照正常的逻辑，我们一般都是从第一个物品开始看，决定选或者不选，然后再去看第二个物品。那么我们现在只看其中一个物品，这个物品无非就两个状态，在背包里，不在背包里。

其实这两个状态就构成了一个状态机。

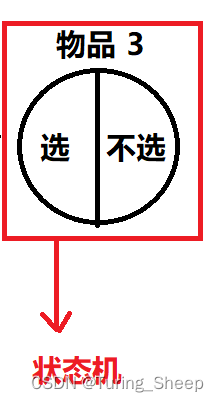
写到这里，我们就可以通俗地理解一下状态机，状态机的作用就是记录一个事件所有可能的存在状态以及这些状态之间的联系。这个作用或许大家现在还会感到一些模糊，但是没关系，后面的例题中作者会进行详细地讲解，让大家深刻体会到。

2、什么是状态机DP

那么什么是状态机DP呢？这种DP方式和之前的DP有什么不同呢？

状态机DP就是在DP数组中专门开辟一个维度记录当前事件所处的状态，比如背包问题如果写成状态机DP的模式，我们会写成$f[i][j][1]$或者$f[i][j][0]$，此时的1代表第i个物品在背包里，0说明第i个物品不在背包里。状态定义可以写作：在前i个物品中选，背包容量为j，且第i个物品在（或者不在）背包中的时候，我们所能携带的最大价值。

其实通过这个例子，大家就能明显地感觉到，在状态机模型中我们强调并记录当前事物的状态。

可是这样做有啥用呢？

作者可以给01背包问题加上一个情景，不能选择相邻的物品。此时如果还按照我们之前的做法，用f[i][j]来定义的话，你对某个物品的具体状态是模糊的。我们一般是用f[i-1][j]和f[i-1][j-v]+w来写转移方程，但是你无法判断第i-1个物品是否在背包里，也就是说你不知道第i-1个物品所处的状态。

但是此时如果按照状态机模型来写，特意强调一下某个物品的状态，我们就可以利用第三维度的0和1来判断能否选当前的物品。

那么此时可以总结一下什么时候用状态机DP，当某个事件的状态影响到后面事件的决策的时候，我们需要在状态定义的时候记录事件状态，即状态机DP。

二、例题

1、AcWing 1049. 大盗阿福

（1）问题

（2）分析

这道题其实就算是一个01背包问题加状态机DP，如果转化为01背包问题的话，即：从1到i个物品里面选，不限制背包容量但是不能够选择相邻物品的情况下，所能携带的最大价值。

a.状态定义

按照刚刚的状态机的解释来看，这道题中把某个店铺看作一个事件，那么抢或者不抢就是这个店铺的状态。而状态机往往也记录了一个事件中各个状态的转移。

但是这里为了解释的更加清楚，我们找到两个相邻的店铺，分别表示出他们的状态，画出状态之间的转移：如下图所示

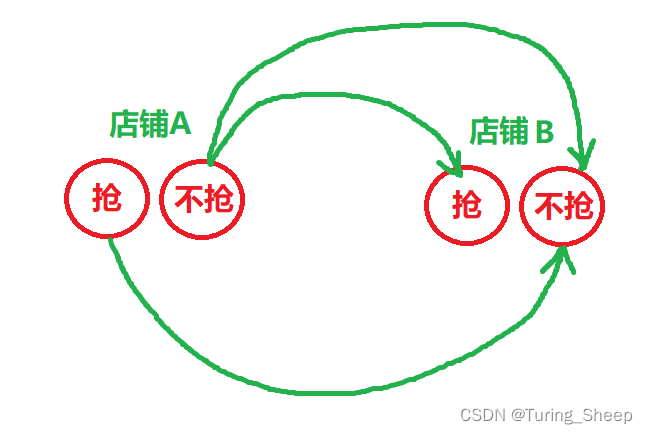
由于题目中强调不能抢相邻的，所以如果我们抢了店铺A，那么下一次就不能抢店铺B，（假设A和B相邻）。

所以我们的f[i][j]表示的是，在前i个店铺里抢劫，且抢（或者不抢）店铺i的情况下，所能抢得的最大价值。0表示不抢，1表示抢。

b.状态转移

上面这个图其实也说明了状态转移方程的书写思路。这里就直接写了。
$$\begin{gathered} f(i,1)=f(i-1,0)+w[i] \\ f(i,0)=max(f(i-1,1),f(i-1,0)) \end{gathered}$$
最后在f(n,1)和f(n,0)中选一个最大值。

c.循环设计

根据转移方程，我们写一个一维的循环即可。

d.初末状态

根据转移方程，我们需要初始化的是两个状态：f[0][0]和f[0][1]。很明显第0个店铺是不存在的，所以f[0][1]是不合法的，初始化为负无穷即可。或者从另一个角度理解，我们的第1个店铺可选可不选，所以第0个店铺一定是不能选的，那么为了不选第0个，只能将f[0][1]变成负无穷。
其实这里不管它也能过，因为店铺的价值最少就是0，虽然这个状态不合法， 但是不影响答案。可是在后续的题目中，初始化会对答案造成一定影响，所以最好还是对不合法的状态进行一定的初始化。

（3）代码

#include<iostream>
using namespace std;
const int N=1e5+10,INF=0x3f3f3f3f;
int w[N],f[N][2];
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        int n;
        cin>>n;
        for(int i=1;i<=n;i++)scanf("%d",w+i);
        f[0][0]=0,f[0][1]=-INF;
        for(int i=1;i<=n;i++)
        {
            f[i][0]=max(f[i-1][0],f[i-1][1]);
            f[i][1]=f[i-1][0]+w[i];   
        }
        cout<<max(f[n][0],f[n][1])<<endl;
    }

    return 0;   
}

2、AcWing 1057. 股票买卖 IV

（1）问题

（2）分析

这道题我们首先得明确一点，我们只有一支股票，只是这支股票在不同天有着不同的价格，因此我们可以把天作为单位划分不同的状态。同时这道题中还有一个关键的信息，同一时刻，我们只能做一次交易，什么意思呢？即当这只股票在我们的手里的时候，我们无法再次进行购买，只能把这个股票卖出或者不卖。如果这支股票不在我们手里，那么我们只能选择买或者不买。

同时，题目还规定，买入股票和卖出股票算一次交易。因此，我们可以认为二者各算半次交易。由于只有手中有股票的时候才能卖出，说明再次之前已经买入。因此，我们可以在卖出股票的时候，把我们的交易次数+1。

a.状态定义

$f[i][j][0]$表示在1到i天中买卖股票，当前已经进行了j次交易，且在第i天里，手中没有当前股票的时候，所得到的最大利润。
$f[i][j][1]$表示在1到i天中买卖股票，当前已经进行了j次交易，且在第i天里，手中有当前股票的时候，所得到的最大利润。

b.状态转移

状态转移的话，我们可以画出下面的图，这样更加清晰：

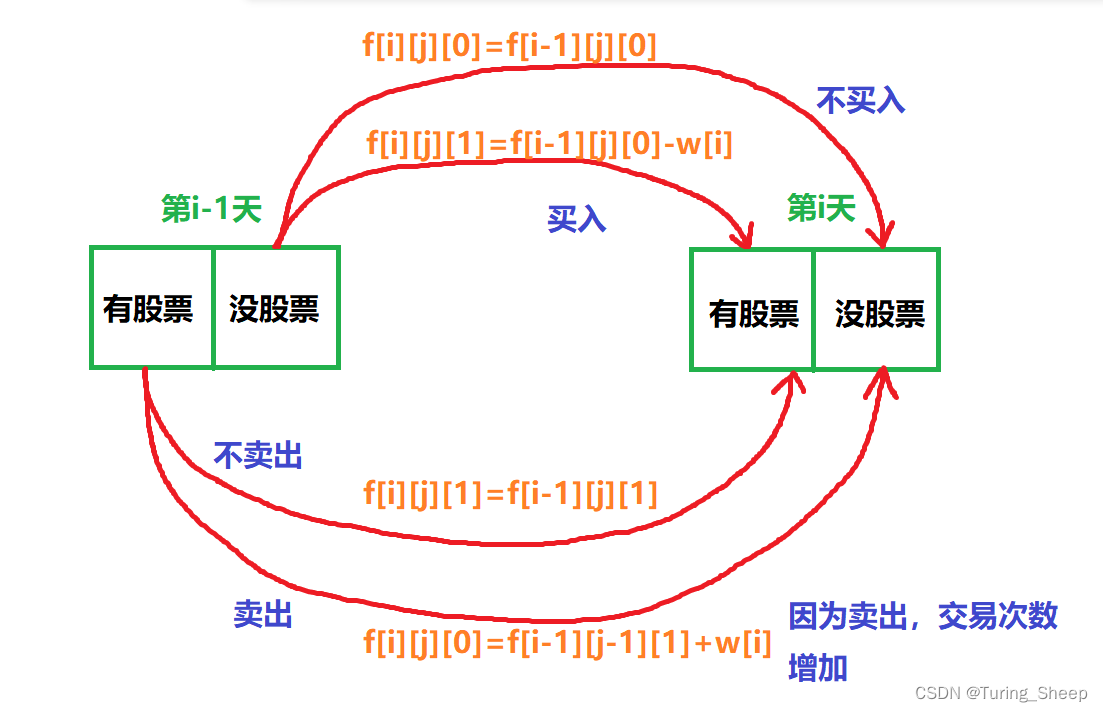
c.循环设计

这道股票的题其实如果不看状态之间的影响的话，其实就是一个01背包，因此我们按照01背包的逻辑来循环即可，即外层循环i，内层循环j。

d.初末状态

这里初始化比较麻烦，因为我们将卖出股票算作一次完整的交易，这一规定使得我们的初始化变得比较复杂。根据我们的规定，f[i][0][1]这种定义也是存在的，即从0到i中选一个最便宜的购入，就是当下的最优解。但是f[0][0][1]是不合法的，因此第0天的股票多贵不知道，没法买，而f[0][0][0]初始化为0即可，这个状态是存在的，第0天的股票虽然不存在，但是我们不买，依旧是0。

如果不想这么复杂的话，我们可以规定买入股票的时候，算一次完整的交易。此时我们发现f[i][0][1]是不合法的了。因为既然有股票，交易次数就不是0了。

（3）代码

规定卖出算一次交易

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,k=110;
int f[N][k][2],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d",w+i);
    memset(f,0xcf,sizeof f);
    f[0][0][0]=0;
    for(int i=1,minv = 1e6;i<=n;i++)
    {
        f[i][0][0]=0;
        minv=min(minv,w[i]);
        f[i][0][1]=-minv;
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j][0]=max(f[i-1][j][0],f[i-1][j-1][1]+w[i]);
            f[i][j][1]=max(f[i-1][j][1],f[i-1][j][0]-w[i]);
        }
    }
    int res=0;
    for(int i=0;i<=m;i++)res=max(f[n][i][0],res); 
    cout<<res<<endl;
    return 0;
}

规定买入算一次交易

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10,k=110;
int f[N][k][2],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d",w+i);
    memset(f,0xcf,sizeof f);
    for(int i=0;i<=n;i++)f[i][0][0]=0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]+w[i]);
            f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][0]-w[i]);
        }
    }
    int res=0;
    for(int i=0;i<=m;i++)res=max(f[n][i][0],res); 
    cout<<res<<endl;
    return 0;
}