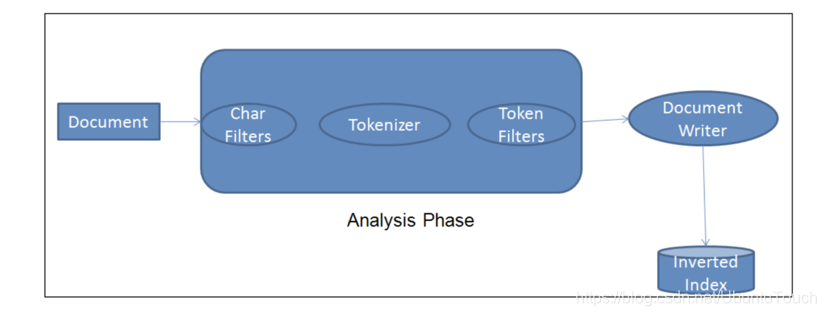
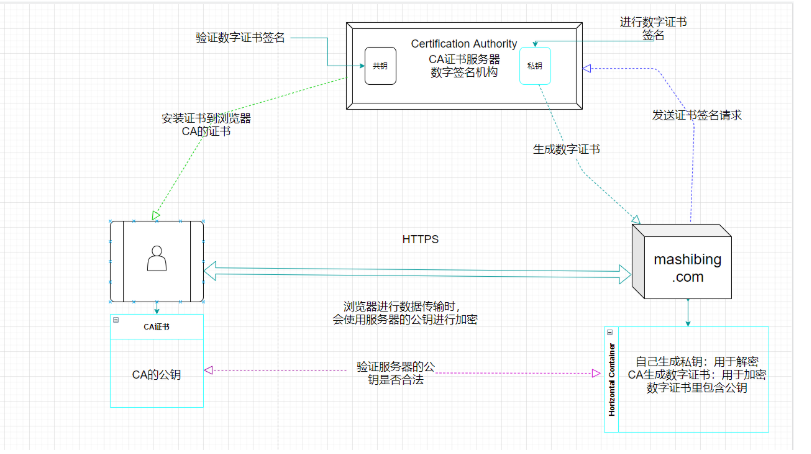
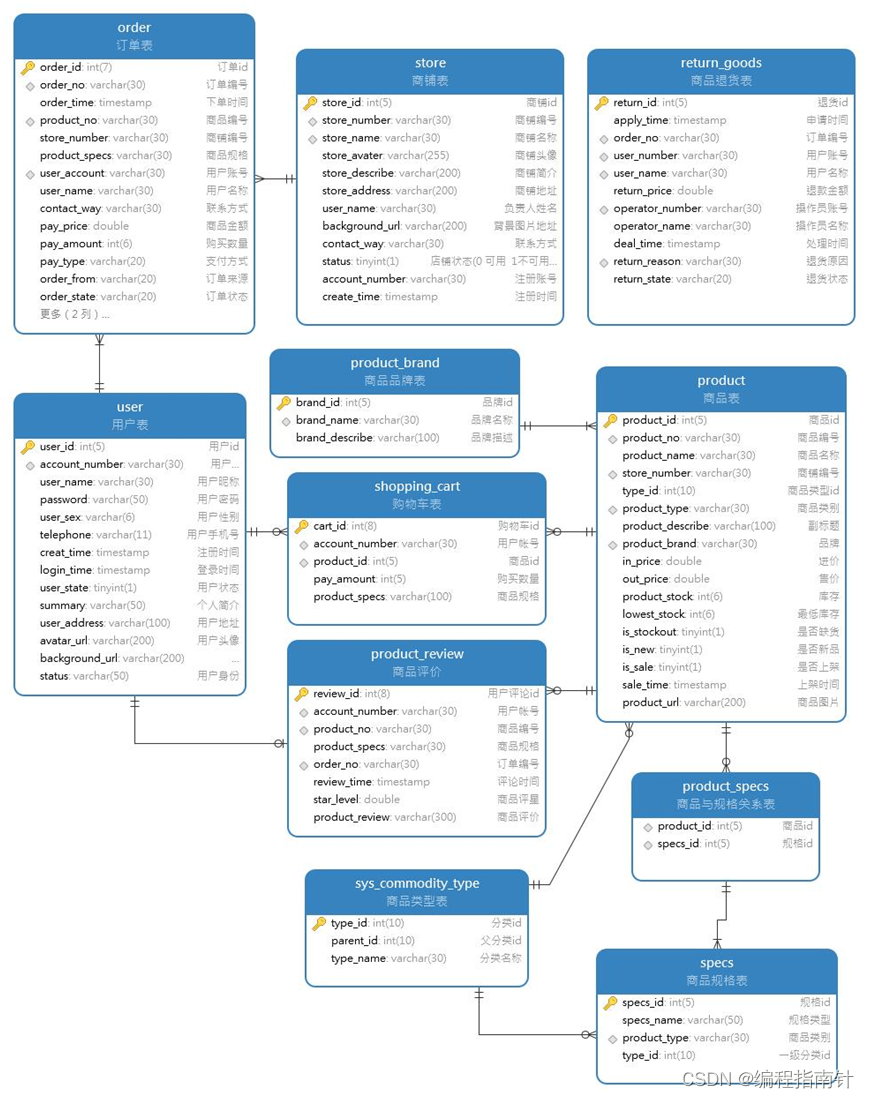
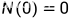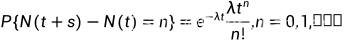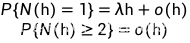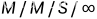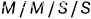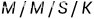• 全国同理:随机过程随机会过 ......

• 唉 你说热统,他为什么要搭配着随机过程一起学 ......

• 唉 你说数模比赛 为什么不能白送一个奖牌

小摘要

泊松过程

• 泊松过程

• 来到间隔与等待时间的分布

• 来到时刻的条件分布

• M/G/1 忙期

• 非齐次泊松过程

• 复合泊松过程

• 条件泊松过程

排队系统

• 输入

• 常见的输入分布

• Poisson

• Erlang

• 排队规则

• 损失制

• 等待制

• 混合制...

• 服务系统

• 服务台工作系统

• 服务时间分布

泊松过程

• 定义计数过程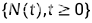为泊松过程,具有参数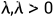,如果

• 

• 过程有独立增量

• 对于任一长度为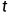的区间中事件的个数服从均值为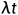的泊松分布

• 

• 其中第三个条件有等价条件:

• 

等待制排队模型(Lingo 辅助求解 下同)

• 输入:参量为\lambda 的 Poisson过程

• 服务时间:服从参数为u的指数分布

• 永远允许排队

三个重要问题

等待概率

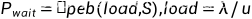
平均等待时间

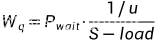
平均逗留时间

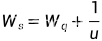
model:
S=3;R=15;T=10/60;load=R*T;
Pwait=@peb(load,S);
W_q=Pwait*T/(S-load);
L_q=R*W_q;
W_s=W_q+T;
L_s=W_s*R;
end

损失制排队模型

六大指标

系统损失概率

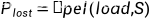
单位时间平均进入系统率

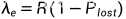
系统相对通过能力与绝对通过能力

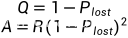
系统在单位时间占用服务台的均值

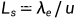
系统服务台的效率

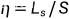
平均逗留时间

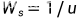
model:
R=200;T=3/60;load=R*T;
P_lost=@pel(load,S);
P_lost<=0.000001;
Q=1-P_lost;
R_e=Q*R;
A=Q*R_e;
L_s=R_e*T;
eta=L_s/S;
min=S;
@gin(S);
end

混合制排队

平衡方程

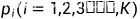指系统有i个顾客的概率

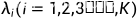指系统在i时刻有i个顾客的概率

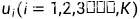指系统在i时刻的服务强度

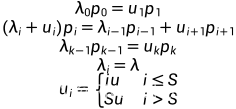
四大指标

系统的损失概率

系统的相对通过能力和单位时间平均进入系统的顾客数

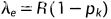
平均队长和平均等待队长

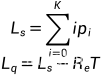
平均逗留时间,平均等待时间

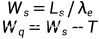
model:

sets:
    state/1..20/:P;
endsets

S=9;K=12;R=4;T=2;
P0*R=1/T*P(1);
(R+1/T)*P(1)=R*P0+2/T*P(2);
@for(state(i)|i#gt#1 #and# i#lt#S:
    (R+i/T)*P(i)=R*P(i-1)+(i+1)/T*P(i+1));
@for(state(i)|i#ge#S #and# i#lt#K:
    (R+S/T)*P(i)=R*P(i-1)+S/T*P(i+1));
R*P(K-1)=S/T*P(K);
P0+@sum(State(i)|i#le#K:P(i))=1;
Plost=P(K);
Q=1-P(K);
R_e=Q*R;
L_s=@sum(state(i)|i#le#K:i*P(i));
L_q=L_s-R_e*T;
W_s=L_s/R_e;
W_q=W_s-T;
end

闭合式排队模型

M/M/S/K/K

model:

S=1;K=6;R=1;T=0.1;
L_s=@pfs(K*R*T,S,K);
R_e=R*(K-L_s);P=(K-L_s)/K;
L_q=L_s-R_e*T;
W_s=L_s/R_e;W_q=W_s-T;
Pwork=R_e/S*T;
end

model:

S=1;K=4;R=1;
L_s=@pfs(K*R/mu,S,K);
max=100*(K-L_s)-75*mu;

end