前端图形开发已成为Web开发绕不开的部分。提升自己前端图形开发能力,才能快点在岗位中突围。但一看到各大实战教程的学习路径就犯难了。
 内容不少,感觉学到老也跳不出来啊。还是走回老路?搞个热门国外开源框架应付算了。
内容不少,感觉学到老也跳不出来啊。还是走回老路?搞个热门国外开源框架应付算了。
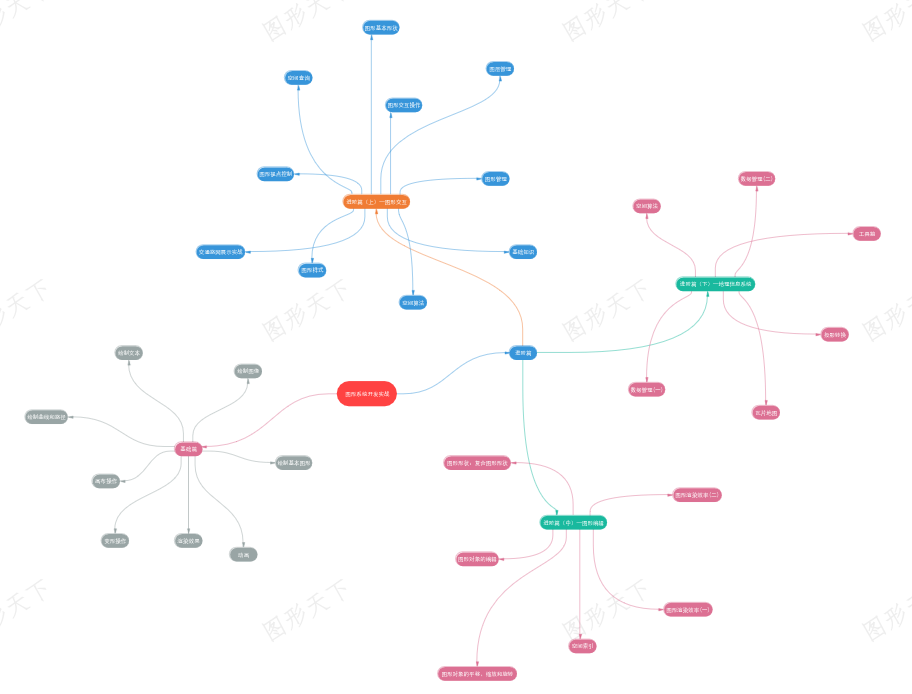
我简单通过对图形系统概述 和 进阶前言 进行阅读。在对比了多个学习资源后,我发现“图形开发学院”的图形开发实战教程与传统的图形开发课程有着显著的区别。
发现该教程是一种与传统学习理论和系统技术指南不同的学习方式——直接面向应用开发,通过项目实战来积累技术,从而缩短学习时间。内容还在持续更新,技术比较接地气,大多能直接与应用项目对接。更有意思的是,不是讲框架应用,而以学习开发一个完全属于自已的图形开发框架为实例!!!
传统的图形开发课程往往侧重于理论知识的讲解,而这实战教程则更加注重通过项目实战来教授知识。在“图形开发学院”网站,能够直接看到大量的实例代码和项目案例,这些案例能够让我更好地理解一些难懂的图形理论。还能够让我,一边学习、一边构建自已的图形开发引擎,在学习过程中积累经验和技能。 抽个时间一口气看看,再分享。