文章目录
- 什么是索引?
- 为什么要引入索引?
- 引入索引的代价
- 操作索引的SQL语句
- 索引背后的数据结构
- B树
- B+ 树
- 回顾思考
- ☁️结语
什么是索引?
数据库中的索引,就相当于一本书的目录。
什么是书的目录?相信大家都并不陌生,一本书最前面的几页,一般就是目录,如果你想找到某个章节,你就可以通过目录快速定位过去。
同理,在数据库中通过索引,我们就可以快速找到要查询的数据(索引的作用)。
为什么要引入索引?
在数据库中 select 这样的查询操作,默认是按照“遍历”的方式,来完成查询的。
比如,指定where语句,条件查询,遍历每一行,把这一行数据代入到条件中,看是否成立,成立就留下,不成立就pass掉。
遍历的复杂度是O(n),但是要注意,此处的每一次取一行,都是要读硬盘的!!虽然也是O(n),但是它和内存操作的O(n)是有本质区别的~~在硬盘上进行操作,比在内存上进行操作,速度要差了好几个数量级呐!!差距还是非常大的。通过一行一行遍历,这样的操作,就会很慢,非常消耗数据库的资源,这也就使数据库能处理的请求量更少了。因此,为了加快查询速度,就需要在数据库中建立索引。
所谓的“索引”就相当于是在数据库中,构建一个特殊的“目录”(一系列特定的数据结构,在硬盘上的),通过这样的数据结构,加快查询的速度,尽可能避免对数据库的遍历操作。
大家应该都用过everything这个软件吧,everything其实就是针对硬盘文件,进行搜索的,那为啥它能查找的这么快?这是因为everything提前把硬盘上的文件数据,构成了特定的数据结构,查询的时候不必遍历了,直接就能进行快速查询。
引入索引的代价
虽然索引这么好,但是也付出了一点的代价。
-
引入索引,需要消耗额外的存储空间。
举个例子来方便理解:假设你有一本词典,词典特别厚(上千页),查词的时候肯定要通过目录来查,这个时候,你仔细观察一下目录的页数,词典的目录 可能就是厚厚的一打。印目录也需要纸张呀~ -
引入索引之后,确实能提高查询的效率,但是可能会影响到增删改的效率。有时候会变慢,比如在进行增删改的时候,需要同步的更新维护索引,更新过程肯定是有额外的开销的;有时候会变快,比如通过条件判断的方式来删除,而删除操作的背后就有查找操作,而索引可以帮我们快速定位;有的时候没有变化。
由此看来,索引这个东西,有利有弊,但是即使如此,我们在实际开发中,还是比较鼓励使用索引的。
原因:
- 存储空间(硬盘)往往不是主要矛盾,大不了多加几个。
- 索引对于增删改也不一定都是负面影响,也可能会触发一些正面效果,另一方面,很多业务场景,查询的频率比增删改要高很多…
操作索引的SQL语句
- 查看索引
show index from 表名;
MySQL会给主键自动生成索引,不需要我们手动创建。
所谓的“索引”是按照 列 的方式来创建的,可以给某个列创建索引,只有在对这个列进行条件查询的时候,索引才能够生效,才能够提升查询速度~~
一个表允许有多个索引(一本词典可能有多种目录(拼音目录、部首目录、笔画目录…))
除了主键之外,unique 和 foreign key 也会自带索引~~这也很容易理解,在子表中插入\修改,需要查询父表;在父表中进行修改\删除,也需要查询子表
- 创建索引
create index 索引名 on 表名(列名);
创建索引也是一个“危险操作”
如果是针对空表,或者表中的数据比较少(几千、几万…),此时创建索引就谈不上危险不危险。
一旦表的数据量比较大,千万级别…此时创建索引操作,就可能会触发大量的硬盘IO,直接把机器就搞的卡死住了,所以一定要在最初创建表的时候,提前规划好这个表要有哪些索引。
如果就是要创建呢?
可以再申请一台机器,将旧库的数据导入到新库当中,等数据全都导入完毕之后,再切换我们访问数据库的那个程序,让他从访问旧库,变成访问新库。
- 删除索引
drop index 索引名 on 表名;
它只能删除,我们自己创建的索引,不能删除MySQL自动生成的(主键、外键、unique…)。
删除索引也是危险操作!!
要能够慎重对待~
索引背后的数据结构
所谓的“构建索引”其实就是引入一些数据结构,对数据进行存储,从而提高查找的速度。
二叉搜索树和哈希表,都不适合给数据库做索引
-
二叉搜索树,最大的问题在于“二叉”要保存的元素多的时候,就会使整个树的高度变的比较高,一旦高度高了,比较次数就会增多~~要知道这是在硬盘上进行的比较,每多比较一次,都是很伤的!!
-
哈希表,最大的问题在于,只能进行“相等”查询,无法进行 > < 这样的“范围查询”,也无法进行like模糊查询。哈希表是要通过哈希函数,把查询的key映射成数组下标,不是说key1 < key2 => hash(key1) < hash(key2);
B树
B+树,为数据库量身定制的数据结构。
要想了解B+树,首先要对B树有一定的了解,B树,也可以写作B - 树(这里 - 不是减号,而是连接符)
B树其实就是N叉搜索树,每个节点,可以有多个子树了(树的度是N)
这样就可以降低树的高度了~每个节点上就不是存储一个key值了,而是多个了

某个节点上保存了N个key就能延伸出N+1个子树了,此时,进行查询的时候,针对每个节点,都需要比较多次,才能确定下一步走哪个区间~~
有人就要问了此时虽然高度降低了,但是每个节点的比较次数变多了,真的能比二叉树有优势吗?
答:其实优势还是很大的!!每个节点,访问的时候是一次硬盘IO就可以了~~
和某个节点进行比较的时候,是先一次硬盘IO,把所有的这个节点上的内容都读取出来,接下来的比较就都是在内存中进行的了
注意:这里的主要目的,不是为了减少比较的次数,而是要减少硬盘IO的次数
B+ 树
B+树是针对B树做出的进一步改进的数据结构~~
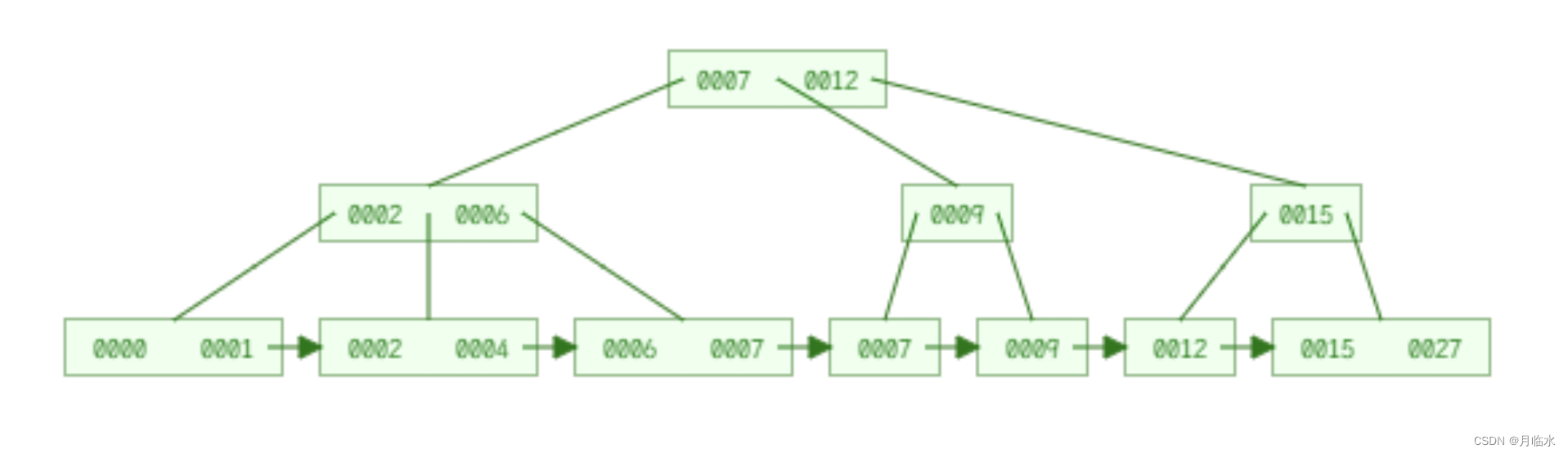
B+树也是N叉搜索树
-
不同于B树,B树是有N个key,划分成N+1个区间,B+树是有N个key,划分出N的区间~
-
父节点中的key值,会在下面的子节点中再次出现(以子节点中的最大值的身份)~~ 重复出现的做法,看起来好像是浪费空间,实际上非常有用~~所有叶子结点,就构成了整个树数据的全集!!
-
B+树把叶子节点,像链表一样首尾相连了~~此时,进行“范围查询”就会非常方便!!
B+ 树的优势:
- N叉搜索树,高度比较低,此时硬盘IO次数就比较少
- 叶子结点是全集,并且用链表结构连接,非常便于进行范围查询~~
- B+树,所有的查询都是要落到叶子结点上完成的~~并且任何一次查询,经历的IO次数和比较次数都是差不多的,查询的开销是稳定的~~(稳定其实是一个很大的优势!!稳定意味着,成本是容易被预估出来的~)
- 由于B+树,叶子结点是全集,非叶子结点上不必存储“数据行”(数据库中的“表”只是一个逻辑上的结构,在物理上并非是一个真正意义的表~物理上就是通过B+树这样的结构来组织的~),只需要存储索引列的key即可。这使得非叶子结点,消耗的空间较少,甚至这样的数据可以直接全部都加载到内存中~~这样又能进一步减少硬盘IO的次数~~
回顾思考
- 索引是啥,它是解决啥问题的?
- 索引付出了什么代价?
- 如何使用 sql 操作索引,是否又注意事项?
- 索引背后的数据结构? => B+树的特点和优势?
解答:
-
索引是啥,它是解决啥问题的?
索引相当于书的目录,能够提高查询的速度 -
索引付出了什么代价?
- 需要更多的存储空间
- 可能会影响增删改的效率(不一定会影响)
整体来说,索引利大于弊,日常开放中还是会经常使用的
-
如何使用 sql 操作索引,是否又注意事项?
- show index from 表名;
查看索引(主键、外键、unique会自动生成索引) - create index 索引名 on 表名(列名);
给指定列创建索引 - drop index 索引名 on 表名;
删除索引 - 索引是针对列来创建的,后续查询的时候,查询条件使用的列和索引列匹配,索引才能生效,才能提高效率。
- 针对一个比较大的表,创建\删除索引,是非常危险的,可能会除法大量的硬盘IO,把机器高挂了
- show index from 表名;
-
索引背后的数据结构? => B+树的特点和优势?
- 特点:
- N叉搜索树,每个节点上包含N个 key,划分出N个区间
- 每个父节点中的元素,都会下沉到子节点中,作为该子节点中最大值的角色来存在
- 叶子结点这一层就构成了数据集合的全集
- 使用类似于链表这样的结构,把叶子节点串起来
- 优势
- N叉搜索树,高度比较低,降低了硬盘IO次数
- 范围查询非常方便和高效
- 所有的查询都落到叶子节点上,开销非常稳定,容易预估成本
- 叶子节点存储数据行,非叶子节点只存储索引列的key值,非叶子节点占据空间小,可以加载到内存中,进一步减少查询时IO的访问次数。
- 特点:
☁️结语
请给自己些耐心,不要急于求成。
山外青山楼外楼,莫把百尺当尽头。
保持空杯心态加油努力吧!
最后的最后,推荐一个数据结构可视化网站,很方便、很好用,很直观。
点击直达 => 数据结构可视化网站
都看到这里啦!真棒(*^▽^*)
可以给作者一个免费的赞赞吗,这将会鼓励我继续创作,谢谢大家
如有纰漏或错误,欢迎指正