目录

问题描述：

实现代码与解析：

回溯：

原理思路：

---

问题描述：

        按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

        给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

        每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

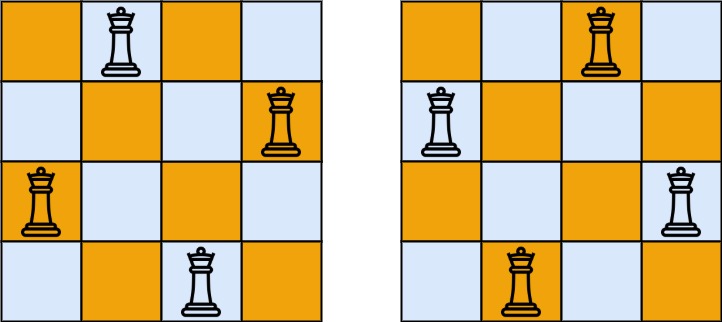
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

实现代码与解析：

回溯：

class Solution {
public:
    //判断位置是否有效
    bool isvaild(int row,int col,int n,vector<string> solveNQueens)
    {
        //列上是否有Q
        for(int i=0;i<row;i++)
        {
            if(solveNQueens[i][col]=='Q')
            {
                return false;
            }
        }
        //左上对角线上是否有Q
        for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--)
        {       
            if(solveNQueens[i][j]=='Q')
            {
                return false;
            }
        }
        //右上对角线上是否有Q
        for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++)
        {       
            if(solveNQueens[i][j]=='Q')
            {
                return false;
            }
        }
        return true;
    }

    vector<vector<string>> result;//记录结果
    //回溯算法
    void backtracking(int n,int row,vector<string> chessboard)
    {
        //全部遍历完了
        if(row==n)
        {
            result.push_back(chessboard);
        }
        for(int col=0;col<n;col++)
        {
            if(isvaild(row,col,n,chessboard))
            {
                chessboard[row][col]='Q';//处理
                backtracking(n,row+1,chessboard);
                chessboard[row][col]='.';//回溯
            }
        }
    }
    vector<vector<string>> solveNQueens(int n) 
    {     
        vector<string> chessboard(n,string(n,'.'));//初始化棋盘上都为点
        backtracking(n,0,chessboard);
        return result;

    }
};

原理思路：

        看起来很难，但其实与其他回溯题差别不大，只不过我们通常是处理一个数组集合，这里我们要处理的是一个二维的集合。我们把每层当作一层循环，每确定一个位置就再向下去寻找下一个位置。

        首先就是确定递归的终止条件，显然就是每层都遍历完就找到结果了。        

        然后就是循环逻辑，我们要写一个判断位置是否有效的函数，来确定此位置是否可以放皇后。根据题目，不能在同一行，同一列，同一斜线的位置，我们可以写出以下代码：

//判断位置是否有效
    bool isvaild(int row,int col,int n,vector<string> solveNQueens)
    {
        //列上是否有Q
        for(int i=0;i<row;i++)
        {
            if(solveNQueens[i][col]=='Q')
            {
                return false;
            }
        }
        //左上对角线上是否有Q
        for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--)
        {       
            if(solveNQueens[i][j]=='Q')
            {
                return false;
            }
        }
        //右上对角线上是否有Q
        for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++)
        {       
            if(solveNQueens[i][j]=='Q')
            {
                return false;
            }
        }
        return true;
    }

        当然在此之前我们要构建一个棋盘初始化放入 ' . ' ，这样可以方便后面我们的输出。

        判断符合条件后，就是开始递归和回溯了。

if(isvaild(row,col,n,chessboard))
{
    chessboard[row][col]='Q';//处理
    backtracking(n,row+1,chessboard);
    chessboard[row][col]='.';//回溯
}