C++ AVL树

news2024/10/5 18:28:37

前言

众所周知红黑树是由AVL树改进得来的，想要深入学习哈希表的底层存储那么AVL的学习就相当有必要了。
本来想将AVL的插入删除都能实现，但是在写删除功能时碰到了难题和Bug，所以暂时先给出插入的实现过程，和删除功能的实现思路

一、插入

1.结构

相比树节点多出两个值：

  • parent 记录父节点
  • blance记录平衡因子
    其中平衡因子代表左子树和右子树的最大深度差
  • 比如blance == 0代表两子树的最大深度相等
    blance == 1 代表右子树最大深度值 比 左子树最大深度值 大一层
    blance == -1 代表右子树最大深度值 比 左子树最大深度值 小一层

树的结构则只保存根节点即可

template<class T>
struct AVLNode
{
	T value;
	AVLNode* left;
	AVLNode* right;
	AVLNode* parent;
	int blance;
	AVLNode(const T& _value)
	{
		value = _value;
		left = nullptr;
		right = nullptr;
		parent = nullptr;
		blance = 0;
	}
};

template<class T>
class AVLTree
{
	typedef AVLNode<T> Node;
	Node* root = nullptr;
}

2.如何实现插入

众所周知，AVL是一棵二叉搜索树，那么这就意味着，在整个树的任意节点处，都存在：

  • 左子树任意值小于本节点，右子树任意节点值大于本节点（已存在的值不插入）
  • 由于上述性质，显而易见我们可以通过判断value值大小的确定插入位置，从根节点开始，层层向下查找
	void insert(const T& value)
	{
		Node* node = new Node(value);
		if (root == nullptr)
		{
			root = node;
			return;
		}
		Node* parent = nullptr;
		Node* cur = root;
		while (cur)
		{
			parent = cur;
			if (cur->value < node->value)
				//较之较大则向右
				cur = cur->right;
			else if (cur->value > node->value)
				//较之较小则向左
				cur = cur->left;
			else//已经相等则不插入
			{
				delete node;
				return;
			}
		}
		node->parent = parent;
		if (parent->value > node->value)
			parent->left = node;
		else
			parent->right = node;
		changeBalanceInsert(node);
	}

3.左右旋转

由二叉树的性质可知，当你插入的值是有序排列时，搜索二叉树的查找性能将会退化成为链表的O(N)级别，为了解决这个问题，AVL树应运而生。
在这里插入图片描述

AVL的最终要的两个性质分别为：中序遍历有序（搜索二叉树）、平衡。
平横是什么呢？
平衡即为：每个节点的两个子树最大深度差绝对值不超过1
例如：下图中标注了所有平衡因子值

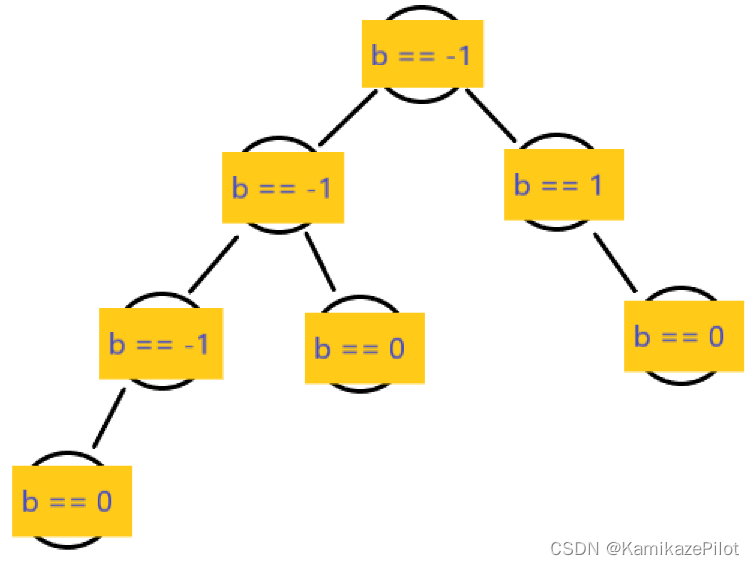
在这里插入图片描述
不平衡：
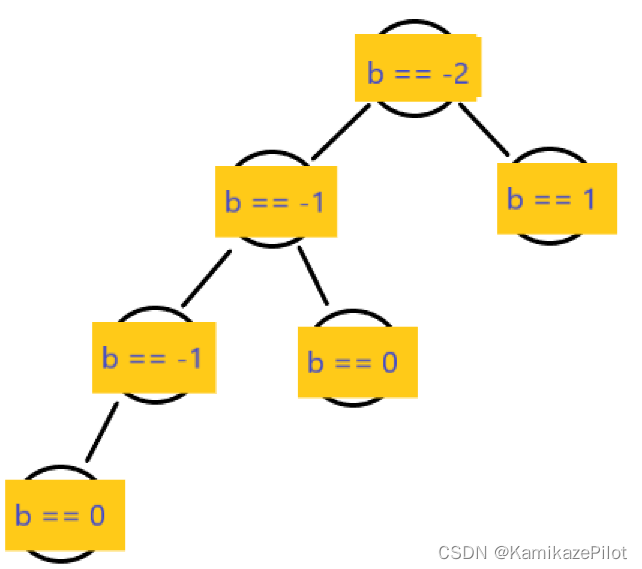
在这里插入图片描述
所有节点中，只要有一个节点失衡，那么该树就不为平衡二叉树
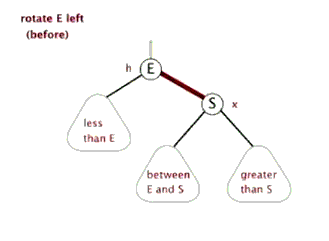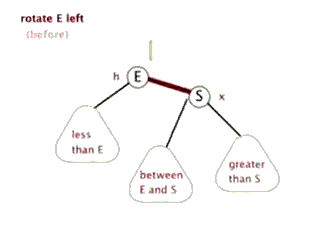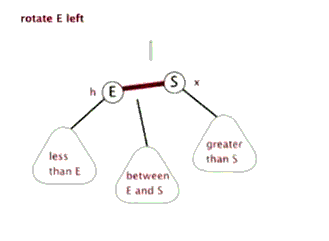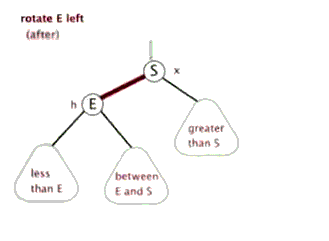
为了保持平衡，AVL引出了左右旋转的概念

  • 左单旋
    请添加图片描述
  • 右单旋
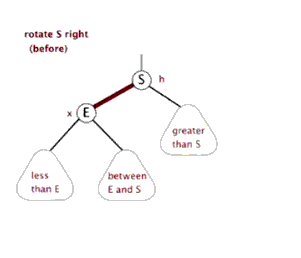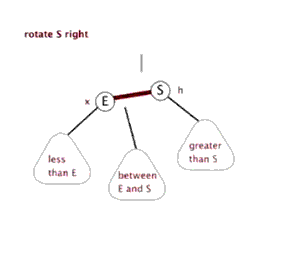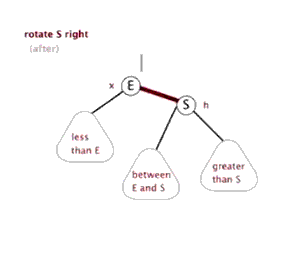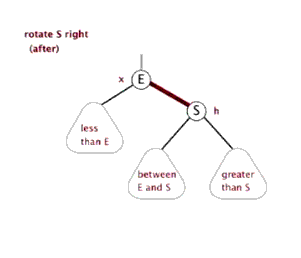
    在这里插入图片描述
    由图可知，每次旋转就是切换一下节点位置和其子节点，做法很简单，共三部
  1. 先将所有可能切换的节点记录下来，例如图中的E，S，between E&S，还有旋转前需改变指向的父节点
  2. 分别更改这三个节点的链接位置
  3. 更新可能改变的平衡因子值
	//右单旋
	void rotateR(Node* node)
	{
		Node* parNode = node->parent;
		Node* leftNode = node->left;
		Node* leftRNode = node->left->right;
		// 切换目标节点左节点的右节点
		if (leftRNode)
			leftRNode->parent = node;
		node->left = leftRNode;
		// 切换目标节点左节点位置
		node->parent = leftNode;
		leftNode->right = node;
		leftNode->parent = parNode;
		if (node == root)
			//是根节点，无父节点
			root = leftNode;
		else if (node == parNode->left)
			//是父节点的左孩子
			parNode->left = leftNode;
		else
			//是父节点的右孩子
			parNode->right = leftNode;

		//调整平衡因子
		node->blance = 0;
		leftNode->blance = 0;
	}
	//左单旋
	void rotateL(Node* node)
	{
		Node* parNode = node->parent;
		Node* rightNode = node->right;
		Node* rightLNode = node->right->left;
		// 切换目标节点右节点的左节点
		if (rightLNode)
			rightLNode->parent = node;
		node->right = rightLNode;

		// 切换目标节点右节点位置
		node->parent = rightNode;
		rightNode->left = node;
		rightNode->parent = parNode;

		// 父节点信息更改
		if (node == root)
			//是根节点
			root = rightNode;
		else if (node == parNode->left)
			//是父节点的左孩子
			parNode->left = rightNode;
		else
			//是父节点的右孩子
			parNode->right = rightNode;

		//调整平衡因子
		node->blance = 0;
		rightNode->blance = 0;
	}

4.双旋

仅靠单旋无法解决所有问题，例如下面
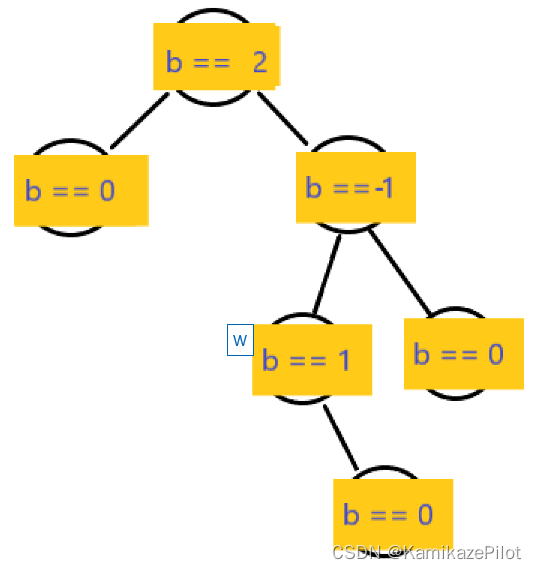
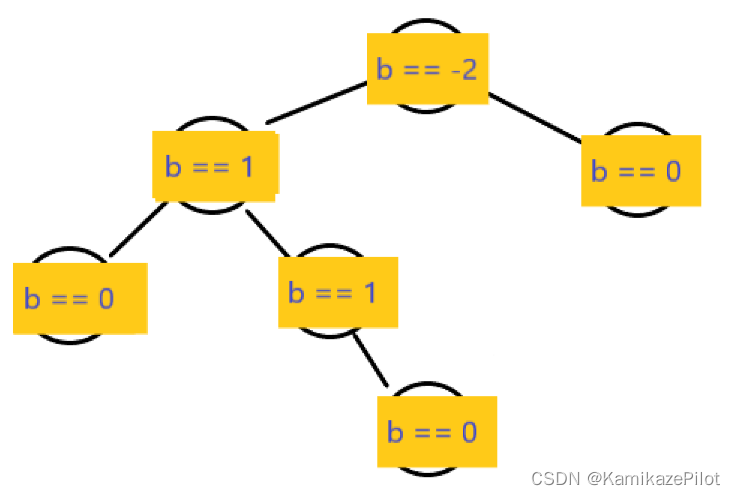
在这里插入图片描述在这里插入图片描述
为了保持平衡，AVL使用的是双旋的解决办法，先将需要旋转的节点的子节点进行旋转调整，再对本节点进行旋转
在这里插入图片描述
先将根节点的右孩子右单旋（先不调整平衡因子）
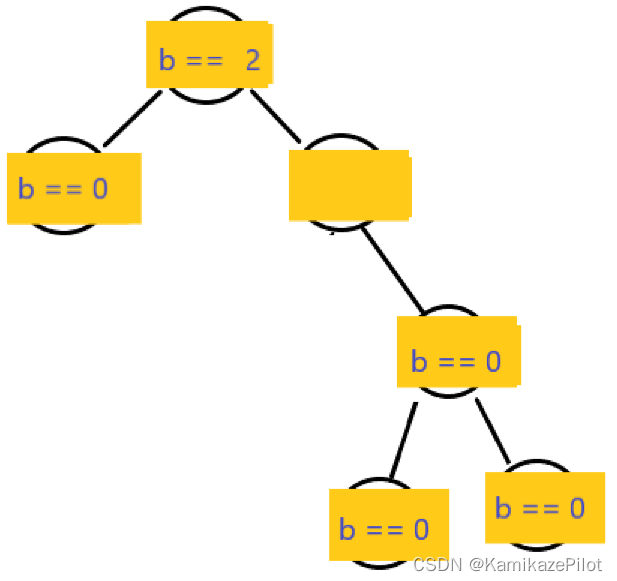
在这里插入图片描述
再将根节点左单旋
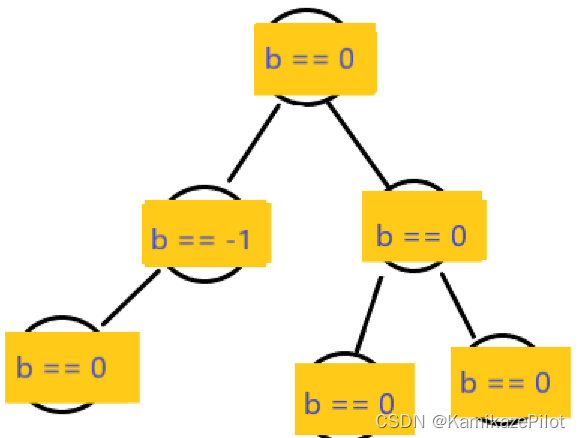
在这里插入图片描述
这种旋转方式为右左双旋，即孩子先向右单旋，再对自己左单旋
左右双旋也是同理

	//左右双旋
	void rotateLR(Node* node)
	{
		Node* leftNode = node->left;
		Node* leftRNode = node->left->right;
		int lRBf = leftRNode->blance;
		rotateL(leftNode);
		rotateR(node);

		node->blance = 0;
		leftNode->blance = 0;
		leftRNode->blance = 0;
		//更改平衡因子
		if (lRBf == 1)
			leftNode->blance = -1;
		else if (lRBf == -1)
			node->blance = 1;
	}

	//右左双旋
	void rotateRL(Node* node)
	{
		Node* rightNode = node->right;
		Node* rightLNode = node->right->left;
		int rLBf = rightLNode->blance;
		rotateR(rightNode);
		rotateL(node);

		node->blance = 0;
		rightNode->blance = 0;
		rightLNode->blance = 0;
		//更改平衡因子
		if (rLBf == 1)
			node->blance = -1;
		else if (rLBf == -1)
			rightNode->blance = 1;
	}

代码

插入完整代码：

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

template<class T>
struct AVLNode
{
	T value;
	AVLNode* left;
	AVLNode* right;
	AVLNode* parent;
	int blance;
	AVLNode(const T& _value)
	{
		value = _value;
		left = nullptr;
		right = nullptr;
		parent = nullptr;
		blance = 0;
	}
};

template<class T>
class AVLTree
{
	typedef AVLNode<T> Node;
	Node* root = nullptr;
	//右单旋
	void rotateR(Node* node)
	{
		Node* parNode = node->parent;
		Node* leftNode = node->left;
		Node* leftRNode = node->left->right;
		// 切换目标节点左节点的右节点
		if (leftRNode)
			leftRNode->parent = node;
		node->left = leftRNode;
		// 切换目标节点左节点位置
		node->parent = leftNode;
		leftNode->right = node;
		leftNode->parent = parNode;
		if (node == root)
			//是根节点
			root = leftNode;
		else if (node == parNode->left)
			//是父节点的左孩子
			parNode->left = leftNode;
		else
			//是父节点的右孩子
			parNode->right = leftNode;

		//调整平衡因子
		node->blance = 0;
		leftNode->blance = 0;
	}

	//左单旋
	void rotateL(Node* node)
	{
		Node* parNode = node->parent;
		Node* rightNode = node->right;
		Node* rightLNode = node->right->left;
		// 切换目标节点右节点的左节点
		if (rightLNode)
			rightLNode->parent = node;
		node->right = rightLNode;

		// 切换目标节点右节点位置
		node->parent = rightNode;
		rightNode->left = node;
		rightNode->parent = parNode;

		// 父节点信息更改
		if (node == root)
			//是根节点
			root = rightNode;
		else if (node == parNode->left)
			//是父节点的左孩子
			parNode->left = rightNode;
		else
			//是父节点的右孩子
			parNode->right = rightNode;

		//调整平衡因子
		node->blance = 0;
		rightNode->blance = 0;
	}

	//左右双旋
	void rotateLR(Node* node)
	{
		Node* leftNode = node->left;
		Node* leftRNode = node->left->right;
		int lRBf = leftRNode->blance;
		rotateL(leftNode);
		rotateR(node);

		node->blance = 0;
		leftNode->blance = 0;
		leftRNode->blance = 0;
		//更改平衡因子
		if (lRBf == 1)
			leftNode->blance = -1;
		else if (lRBf == -1)
			node->blance = 1;
	}

	//右左双旋
	void rotateRL(Node* node)
	{
		Node* rightNode = node->right;
		Node* rightLNode = node->right->left;
		int rLBf = rightLNode->blance;
		rotateR(rightNode);
		rotateL(node);

		node->blance = 0;
		rightNode->blance = 0;
		rightLNode->blance = 0;
		//更改平衡因子
		if (rLBf == 1)
			node->blance = -1;
		else if (rLBf == -1)
			rightNode->blance = 1;
	}

	//插入时更改平衡性
	void changeBalanceInsert(Node* cur)
	{
		Node* parent = cur->parent;
		while (cur->parent)
		{
			parent = cur->parent;
			//更新平衡因子
			parent->blance += cur == parent->left ? -1 : 1;
			//平衡时不再向上
			if (parent->blance == 0)
				break;
			else if (parent->blance == 1 || parent->blance == -1)
				cur = parent;
			// 需要旋转
			else if (parent->blance == -2)
			{
				if (parent->left->blance == -1)//右单旋
					rotateR(parent);
				else//左右单旋
					rotateLR(parent);
				break;
			}
			else if (parent->blance == 2)
			{
				if (parent->right->blance == 1)//左单旋
					rotateL(parent);
				else//右左单旋
					rotateRL(parent);
				break;
			}
		}
	}

public:
	void insert(const T& value)
	{
		Node* node = new Node(value);
		if (root == nullptr)
		{
			root = node;
			return;
		}
		Node* parent = nullptr;
		Node* cur = root;
		while (cur)
		{
			parent = cur;
			if (cur->value < node->value)
				//较之较大则向右
				cur = cur->right;
			else if (cur->value > node->value)
				//较之较小则向左
				cur = cur->left;
			else//已经相等则不插入
				return;
		}
		node->parent = parent;
		if (parent->value > node->value)
			parent->left = node;
		else
			parent->right = node;
		changeBalanceInsert(node);
	}
	//下面的都是测试方法
	//获取最大深度
	int getDepth(Node* node)
	{
		if (node == nullptr) return 0;
		return max(getDepth(node->left), getDepth(node->right)) + 1;
	}

	//打印整棵树
	void printAll()
	{
		if (root == nullptr) return;
		int depth = getDepth(root);
		vector<vector<Node*>> container(depth);
		//遍历存储
		for (int i = 0; i < depth; ++i)
		{
			if (i == 0)
			{
				container[0].push_back(root);
				continue;
			}
			for (Node* ele : container[i - 1])
			{
				if (ele == nullptr)
				{
					container[i].push_back(nullptr);
					container[i].push_back(nullptr);
				}
				else
				{
					container[i].push_back(ele->left);
					container[i].push_back(ele->right);
				}
			}
		}

		system("cls");
		//打印
		for (int i = 0; i < depth; ++i)
		{
			int sp = (1 << (depth - 1 - i)) + (container[depth - 1].size() / container[i].size() - 1);
			separator(sp);
			for (int j = 0; j < container[i].size(); ++j)
			{
				if(j != 0)
					separator(2 * sp);
				if (container[i][j])
				{
					cout << container[i][j]->value;
					if (container[i][j]->value < 10)
						separator(1);
				}
				else
				{
					separator(2);
				}
			}
			cout << endl;
		}

	}
	//打印间隔
	void separator(int num)
	{
		for (int i = 0; i < num; ++i)
			cout << ' ';
	}
}

二、删除

删除的基本思路是，如果被删除节点有孩子，则将其不断向下交换，直到交换到没有孩子为止
如果没有孩子，则可以将其直接删除，再向上调整整棵树。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/179986.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【日常系列】LeetCode《29·动态规划4》

【日常系列】LeetCode《29·动态规划4》

数据规模->时间复杂度 <10^4 &#x1f62e;(n^2) <10^7:o(nlogn) <10^8:o(n) 10^8<:o(logn),o(1) 内容 字符串/数组dp问题 动态规划中的双状态问题 lc 139【top100】&#xff1a;单词拆分 https://leetcode.cn/problems/word-break/ 提示&#xff1a; 1 <…
阅读更多...
Qt扫盲-QHttpPart类理论总结

Qt扫盲-QHttpPart类理论总结

QHttpPart类理论总结一、概述二、使用1. 设置头2. 设置内容一、概述 QHttpPart类保存一个主体部分&#xff0c;用于HTTP multipart MIME消息中(由QHttpMultiPart类表示)。 QHttpPart由一个头块和一个数据块组成&#xff0c;它们由两个连续的新行相互分隔。一个部分的例子是: …
阅读更多...
智能合约开发——Sui/Move vs. Solana/Rust

智能合约开发——Sui/Move vs. Solana/Rust

1. 引言 前序博客有&#xff1a; zkMove——针对Move合约生态的zkVM 定位为高性能L1的Aptos和Sui&#xff0c;均采用Move合约编程语言。Solana也定位为高性能L1&#xff0c;但其采用Rust合约编程语言。本文重点对比Sui/Move和Solana/Rust合约编程语言。【Aptos/Move为不同的M…
阅读更多...
三、Java框架之SpringMVC1_MVC基础

三、Java框架之SpringMVC1_MVC基础

文章目录1. SpringMVC简介1.1 回顾Servlet技术1.2 SpringMVC入门案例步骤1&#xff1a;创建javaweb项目&#xff0c;并导入jar包步骤2&#xff1a;创建Controller步骤3&#xff1a;创建SpringMVC的配置文件步骤4&#xff1a;使用配置类替换web.xml步骤5&#xff1a;启动项目并访…
阅读更多...
PyTorch深度学习实践第二讲线性模型

PyTorch深度学习实践第二讲线性模型

目录监督学习四步骤线性模型泛化代码作业监督学习四步骤 DataSet&#xff08;数据集&#xff09;Model&#xff08;模型选择和设计&#xff0c;例如神经网络&#xff0c;决策树等&#xff09;Training&#xff08;大部分模型都需要训练&#xff0c;都有些例如KNN不需要训练&am…
阅读更多...
BFS（四）127. 单词接龙、433. 最小基因变化

BFS（四）127. 单词接龙、433. 最小基因变化

目录 127. 单词接龙 433. 最小基因变化 127. 单词接龙 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk&#xff1a; 每一对相邻的单词只差一个字母。 对于 1 < i < k 时&am…
阅读更多...
Qt 6.x中Qt Quick简介及示例

Qt 6.x中Qt Quick简介及示例

Qt Quick首次在Qt 4.7和Qt Creator 2.1中引入&#xff0c;是一种高级UI技术。 Qt Quick模块是用于编写QML(Qt Meta-Object Language, Qt元对象语言)应用程序的标准库。Qt QML模块提供了QML引擎(engine)和语言基础设施&#xff0c;而Qt Quick模块提供了使用QML创建用户界面…
阅读更多...
LCD timing的理解

LCD timing的理解

前言 LCD的时序，之前也有介绍过（深入裸机），但是在介绍这些参数的时候是以感性的认识去理解的，而且多少有些错误，我们以内核文档中的描述为准（Documentation/fb/framebuffer.txt），在结合全志平台来重新正确的理解这些参数。 我们在看下文档中的解释: The frame buffe…
阅读更多...
【学习笔记】智能合约引擎

【学习笔记】智能合约引擎

图片来源&#xff1a;https://www.researchgate.net/publication/336453428_Detecting_nondeterministic_payment_bugs_in_Ethereum_smart_contracts/figures?lo1智能合约是区块链技术的核心。我们可以根据以下公式定义智能合约智能合约事务处理和保存机制完备的状态机智能合约…
阅读更多...
【手写 Promise 源码】第一篇 - Promise 简介

【手写 Promise 源码】第一篇 - Promise 简介

一&#xff0c;前言 上一篇&#xff0c;完成了 Promise 源码学习的目录&#xff1b; 本篇&#xff0c;主要对 Promise 进行简单的概括介绍&#xff1b; 二&#xff0c;Promise 简介 Promise 是一个类或构造函数&#xff0c;是 JS 原生提供的&#xff0c;通过实例化 Promise …
阅读更多...
【Java】还不懂this关键字？一分钟彻底弄懂this关键字

【Java】还不懂this关键字？一分钟彻底弄懂this关键字

博主简介&#xff1a;努力学习的预备程序媛一枚~博主主页&#xff1a; 是瑶瑶子啦所属专栏: Java岛冒险记【从小白到大佬之路】 前言 问题&#xff1a;为什么会存在this? 在上一篇【JavaSE】一文看懂构造器/构造方法&#xff08;Cunstructor&#xff09;中&#xff0c;我们已…
阅读更多...
更方便Spring存储和读取对象，五大类注解、@Bean、@Autowired、@Resource

更方便Spring存储和读取对象，五大类注解、@Bean、@Autowired、@Resource

上一篇博客我们介绍了如何使用xml来引入bean对象&#xff0c;当项目多的时候&#xff0c;显然那样是比较麻烦的。现在我们只需要 个注解就可以替代了。注意&#xff1a;注解和xml可以同时使用准备工作:配置扫描路径我们需要配置 下存储对象的扫描包路径&#xff0c;只有被配置的…
阅读更多...
利用Windows系统服务进行权限提升

利用Windows系统服务进行权限提升

提权是后渗透重要的一环节&#xff0c;如果当前获取的用户权限比较低&#xff0c;那么我们将无法访问受保护的系统资源或执行系统管理操作&#xff0c;影响后续的攻击过程。这要求我们通过各种手段将当前用户的权限进行提升&#xff0c;以满足后续攻击的要求。利用系统服务提权…
阅读更多...
VUE2--22.11.23

VUE2--22.11.23

VUE2一、Vue.js devtools二、Vue简介1、什么是Vue2、Vue的特性1.数据驱动视图2.双向数据绑定3.MVVM三、Vue的基本使用1、基本使用步骤四、Vue的指令与过滤器1、什么是指令2、内容渲染指令1.v-text2.{{}}3.v-html3、属性绑定指令4、事件绑定指令5、双向绑定指令6、条件渲染指令7…
阅读更多...
【Linux】动静态库、文件的三个时间

【Linux】动静态库、文件的三个时间

1.文件的三个时间Access: 访问时间&#xff0c;访问的频率很高&#xff0c;所以较新的Linux都是按一定的时间间隔刷新Modify: 修改文件内容时间Change:修改文件属性时间&#xff0c;修改文件内容也会修改文件属性makefile自动编译判断文件是否为最新&#xff1a;就是按可执行程…
阅读更多...
运动基元（一）：Dubin‘s曲线【part3】

运动基元（一）：Dubin‘s曲线【part3】

3.5 RLR RLR的第一段圆弧的曲率 k 1 = − k m a x < 0 → s i g n ( k 1 ) = − 1 k_1=-k_{max}<0\rightarrow si
阅读更多...
Springboot图书馆图书借阅管理系统x1x74

Springboot图书馆图书借阅管理系统x1x74

目 录 1 概述 1 1.1课题背景及意义 1 1.2 国内外研究现状 1 1.3 本课题主要工作 2 2 系统开发环境 3 2.1 java简介 3 2.2 Mysql数据库 3 2.3 B/S结构 4 2.4 JSP技术介绍 4 3 系统分析 5 3.1 可行性分析 5 3.1.1 技术可行性 5 3.1.2操作…
阅读更多...
机器学习sklearn笔记：LDA（线性判别分析）

机器学习sklearn笔记：LDA（线性判别分析）

1 介绍 1.有监督的降维2.投影后类内方差最小&#xff0c;类间方差最大2 推导 我们记最佳的投影向量为w&#xff0c;那么一个样例x到方向向量w上的投影可以表示为&#xff1a; 给定数据集令分别表示第i类的样本个数、样本集合、均值向量和协方差矩阵——>在投影上的均值是 —…
阅读更多...
kafka初识

kafka初识

安装kafka 下载 下载window的kafka地址 window的kafka只是为了方便学习 安装地址&#xff1a;kafka.apache.org/ 安装 解压zip为文件夹 启动kafka kafka服务器的功能相当于RocketMQ中的broker&#xff0c;kafka运行还需要一个类似于命名服务器的服务。在kafka安装目录中自…
阅读更多...
Windows10添加WebDav地址时报错“输入的文件夹无效，请选择另一个”

Windows10添加WebDav地址时报错“输入的文件夹无效，请选择另一个”

一、问题描述在使用Windows10添加WebDav网络地址时&#xff0c;报错“输入的文件夹无效&#xff0c;请选择另一个”&#xff0c;如下图所示&#xff1a;二、问题分析这是由于Windows10的WebDav默认只支持https协议&#xff0c;没有支持http协议导致的。三、解决办法3.1、修改注…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023