目录
127. 单词接龙
433. 最小基因变化
127. 单词接龙
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
示例 1:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。示例 2:
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出:0
解释:endWord "cog" 不在字典中,所以无法进行转换。
题目要求一次只能改变一个字符,那就hit来说可以改变的方案就是h i t分别进行改变,三个字符,每个单词改变25次,如果单词再长一些,我这个血压一下就上去了。那么主要思想就是这样,就是这样一股脑的处理单词,然后查找单词
普通的find肯定时间复杂度一下嗡的就上去了,所以这里就要借助哈希了,用哈希表高效的查找来优化时间。
set<string> words(wordList.begin(), wordList.end()); 初始化俩个哈希set
set<string> book; 一个用来访问单词序列,一个用来标记访问过得元素如何处理?
一个for循环从当前单词起始位置一直访问到单词结束位置
如何查找?
具体操作就在上述for循环下在加入一个for循环从'a'到‘z’ 进行当前单词位的修改!!! 其中不免会出现重复,所以引入一个book来处理重复问题
for(int i = 0; i < curStr.size(); i++)
{
string str1 = curStr;
for(char ch = 'a'; ch <= 'z'; ch++)
{
str1[i] = ch; // 对该位进行修改
如果单词存在于单词序列中并且没有被使用过。
if(words.find(str1) != words.end()
&& book.find(str1) == book.end())
{
q.push(str1);
book.insert(str1);
}
}
}源码:
class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
set<string> words(wordList.begin(), wordList.end()); //初始化俩个哈希set
set<string> book; // 一个用来访问单词序列,一个用来标记访问过得元素
queue<string> q;
q.push(beginWord); // 队列中放入begin
book.insert(beginWord);
int step = 1; //序列个数
while(!q.empty())
{
int size = q.size();
while(size--)
{
string curStr = q.front();
q.pop();
if(curStr == endWord)
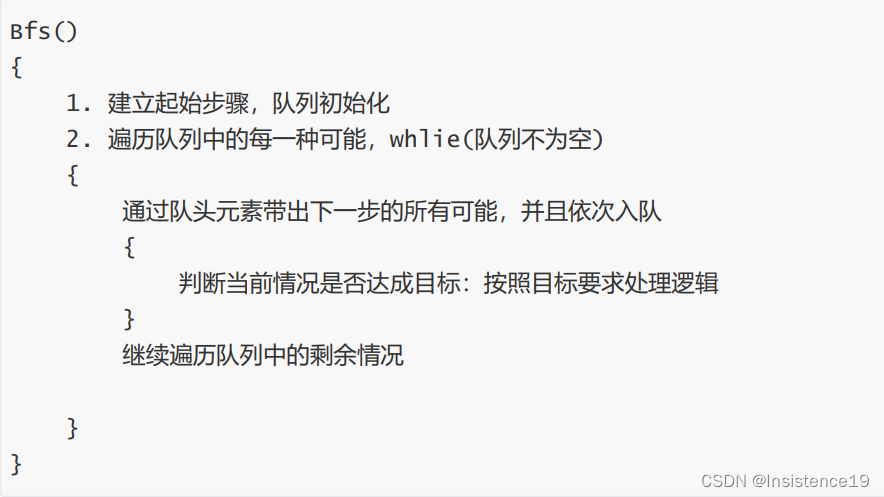
return step; //自此往上都是BFS经典模板
for(int i = 0; i < curStr.size(); i++)
{
string str1 = curStr;
for(char ch = 'a'; ch <= 'z'; ch++)
{
str1[i] = ch;
if(words.find(str1) != words.end()
&& book.find(str1) == book.end())
{
q.push(str1);
book.insert(str1);
}
}
}
}
step++;
}
return 0;
}
};433. 最小基因变化
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
例如,"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。
示例 1:
输入:start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出:1
class Solution {
public:
int minMutation(string startGene, string endGene, vector<string>& bank) {
set<string> banks(bank.begin(), bank.end());
set<string> book;
queue<string> q;
q.push(startGene);
book.insert(startGene);
char base[4] = {'A','G','C','T'};
int step = 0;
while(!q.empty())
{
int size = q.size();
while(size--)
{
string curStr = q.front();
q.pop();
if(curStr == endGene) // 以上均为模板
return step;
for(int i = 0; i < 8; i++) // 一个序列只有8个符号
{
string str1 = curStr;
for(int j = 0; j < 4; j++) // 对于每一种符号有4中变幻
{
str1[i] = base[j];
if(banks.find(str1) != banks.end()
&& book.find(str1) == book.end())
{
q.push(str1);
book.insert(str1);
}
}
}
}
step++;
}
return -1;
}
};