监督学习四步骤

DataSet（数据集）
Model（模型选择和设计，例如神经网络，决策树等）
Training（大部分模型都需要训练，都有些例如KNN不需要训练）
Inferring（推导使用）

线性模型

假设一个学生每周花费x小时在学习上，那么他可能会在最终测验上取得y分。

x	y
1	2
2	4
3	6
4	?

模型绘制
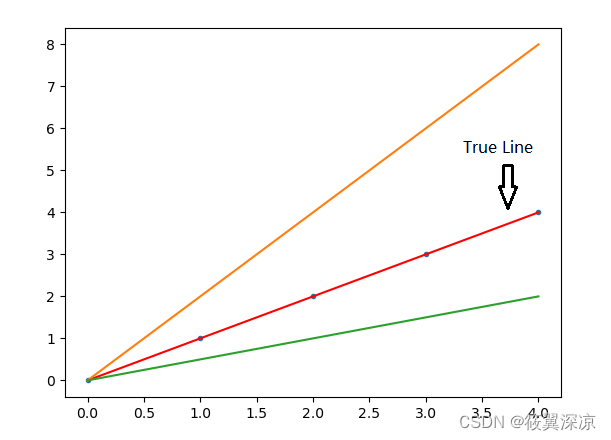
进行猜测之后可能为

$\hat{y}=x * w + b$
$\hat{y}=a * x ^ 2 + b * x + c$
$\hat{y}=a * e ^ {bx} + c$

经过观测后为 $\hat{y}=x * w + b$ ，简化后为 $\hat{y}=x * w$
我们不知道权重w是多少扫，因此需要对结果做出评估：

Train Loss (Error)
$loss=(\hat{y} - y) ^ 2 = (x * w - y)^2$

评估模型被称之为Loss损失。
目标是找到权重w使得每个点的平均损失最小，因此：

针对样本	Train Loss (Error)	$loss=(\hat{y} - y) ^ 2 = (x * w - y)^2$
针对Training Set	Mean Square Error => MSE	$cost=\frac{1}{N} \sum^{N}_{n=1} (\hat{y_n} - y_n)^2$

泛化

当我们获得数据集时将其分为训练集和测试集，其中训练集数据是不可见的。
数据集划分
因此训练完模型之后我们可能不一定符合 $(x, y)$ 的分布，也有可能太过于符合，将噪声也学习进去造成过拟合。显然这不是我们希望看到的，我们应当希望看到我们的模型具有一定的泛化能力，也就是对于没训练过的数据也有较好的识别能力。所以我们要将训练集进行分离。
训练集划分
当在训练集上训练完后再使用开发集进行评估，使得模型具有一定的泛化能力。

代码

# @Filename: LinearModel.py
# @Time    : 2023/1/26 13:09
# @Author  : 筱翼深凉

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]


# 计算预测值
def forward(x):
    return x * w


# 计算误差
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


w_list = []
mse_list = []
for w in np.arange(0.0, 4.0, 0.1):
    print('w=', w)
    loss_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)  # 计算预测值
        loss_val = loss(x_val, y_val)  # 计算误差
        loss_sum += loss_val
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', loss_sum / 3)
    w_list.append(w)
    mse_list.append(loss_sum / 3)
plt.plot(w_list, mse_list)
plt.xlabel('w')
plt.ylabel('LOSS')
plt.show()

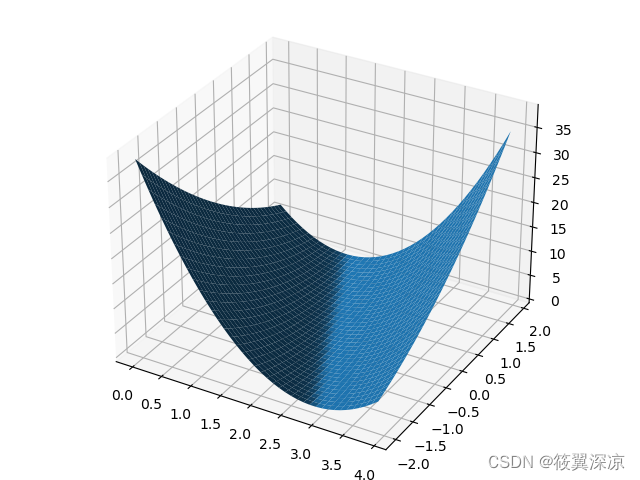
作业

# @Filename: Exercise.py
# @Time    : 2023/1/26 13:36
# @Author  : 筱翼深凉
"""
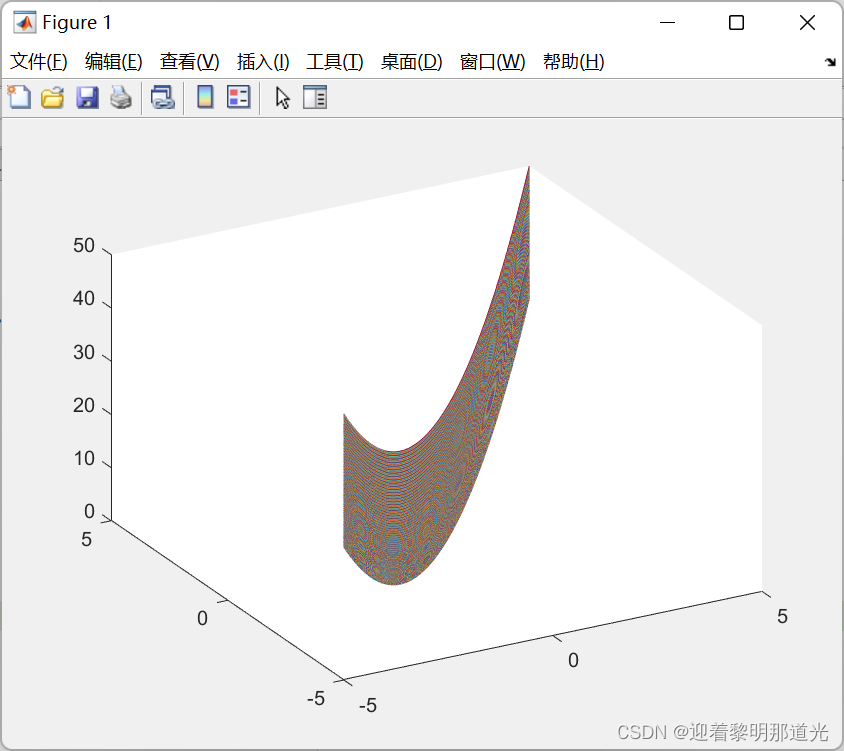
    将模型更换为 y = w * x + b
"""

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]


# 计算预测值
def forward(x):
    return x * w + b


# 计算误差
def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


W = np.arange(0, 4, 0.1)
B = np.arange(-2, 2, 0.1)
[w, b] = np.meshgrid(W, B)

loss_sum = 0
for x_val, y_val in zip(x_data, y_data):
    y_pred_val = forward(x_val)  # 计算预测值
    loss_val = loss(x_val, y_val)  # 计算误差
    loss_sum += loss_val
print('MSE=', loss_sum / 3)
MSE = loss_sum / 3

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(w, b, loss_sum / 3)
plt.show()