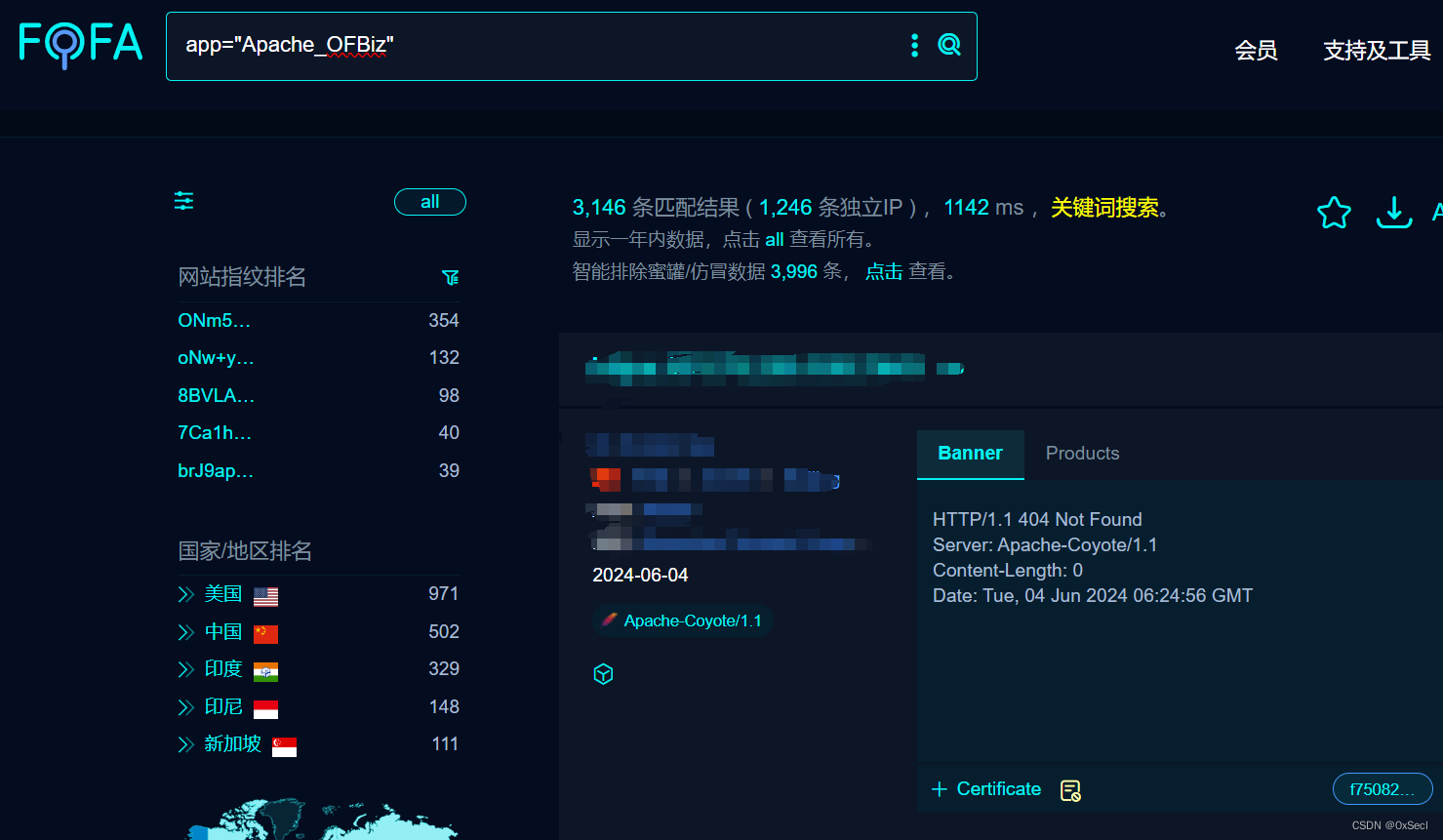
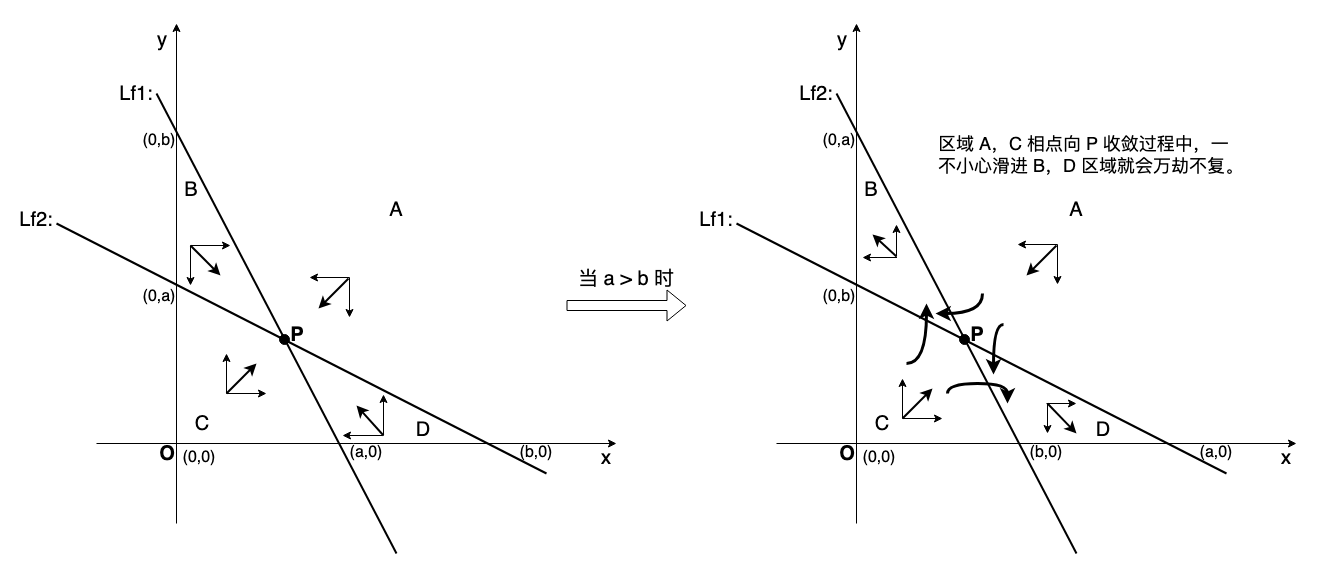
接着昨天的问题,inflight 守恒的模型一定存在稳定点吗?并不是。如果相互抑制强度大于自我抑制强度,系统也会跑飞:
模拟结果如下:
所以一定要记得 a < b。
比对前两个图和后两个图的 a,b 参数关系,即可得道。接下来的问题是,即使 a < b,这一切图景,是一厢情愿吗?对于一种端到端 capacity-seeking 算法的衍生,震荡是本质属性,E_best = max(bw / delay) 共识又何德何能?
抛开 E_best 共识本身,先论证稳定收敛点的存在性,这是一个典型的资源消耗模型,但更简单些。系统表达如下,设 x 为流量,y 为带宽和 buffer 等承载流量的资源,则有:
d
x
d
t
=
a
∗
y
−
b
∗
x
\dfrac{dx}{dt}=a*y-b*x
dtdx=a∗y−b∗x
d
y
d
t
=
−
c
∗
x
∗
y
+
d
∗
x
\dfrac{dy}{dt}=-c*x*y+d*x
dtdy=−c∗x∗y+d∗x
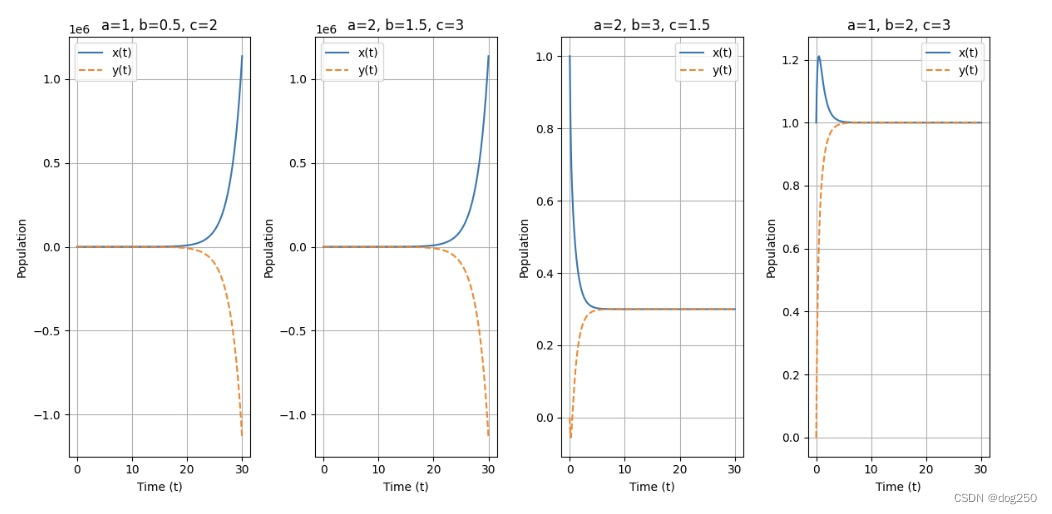
x 的变化受两方面影响,它的生成速度与资源成正比,同时其消亡速度与其本身成正比,而资源 y 也受两方面影响,首先,更多的 x 会消耗更多资源,更充足的 y 会使其消耗更快(本性?),其次,如果有 x 退出,y 会增长。模拟结果如下:
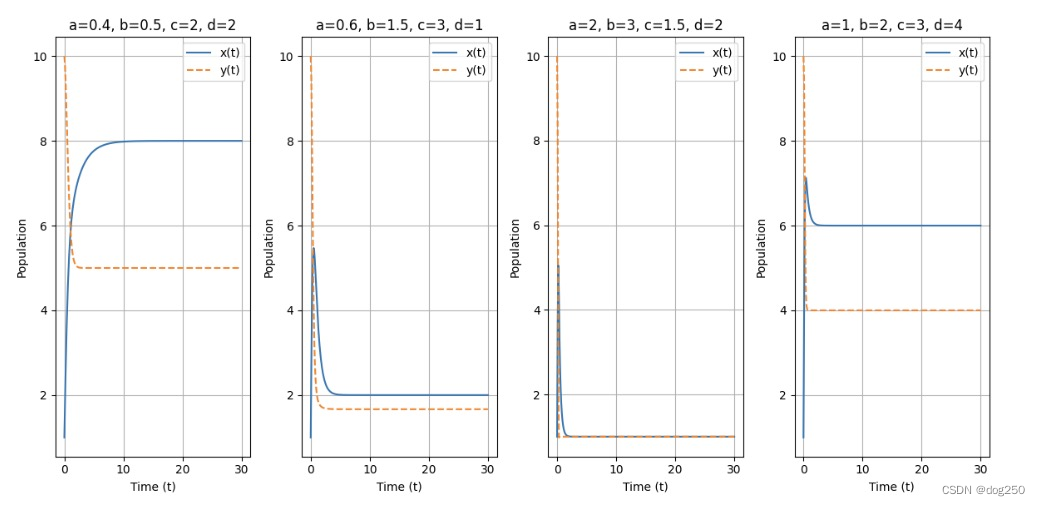
都可以稳定收敛。注意图 1 的参数,它甚至没有震荡。
就着这个模拟,说点有趣的,把系统稍微变一下,如果资源可再生,而不是守恒,系统表达式的 y 将是:
d y d t = − c ∗ x ∗ y + d ∗ y \dfrac{dy}{dt}=-c*x*y+d*y dtdy=−c∗x∗y+d∗y
看下会怎样:
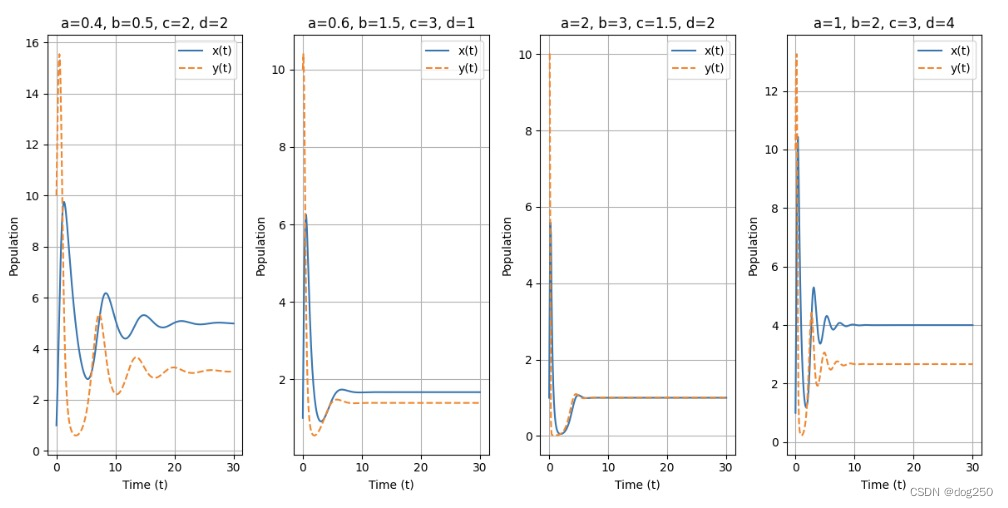
系统竟然震荡了,且资源利用率并不高。所以,基于守恒,自己玩自己,只要调得一手好参数,不愁不高效。只要 E_best 共识被识别,流量守恒,资源守恒,不断腾挪(想象一下,早高峰的公交车刚开始非常拥挤,晃荡一阵子后就不拥挤了,但也上不来人了),最终就是效率和公平双百分。
再说个敏感的,如果资源不可再生,已消费资源不可腾挪重归资源池,且消费者有趋之若鹜的倾向呢?比如看到人越多就越去凑热闹,x 将改为:
d x d t = a ∗ c ∗ x ∗ y − b ∗ x \dfrac{dx}{dt}=a*c*x*y-b*x dtdx=a∗c∗x∗y−b∗x
结果如下:

像不像安得广厦千万间,大庇天下寒士俱欢颜的奢望,到底是鸡飞蛋打一场空,越是疯狂越是奔赴,最终延迟的报应越猛烈,双归零。
浙江温州皮鞋湿,下雨进水不会胖。