机器学习【西瓜书/南瓜书】--- 第四章决策树

一、决策树理论分析

1.1 通俗理解

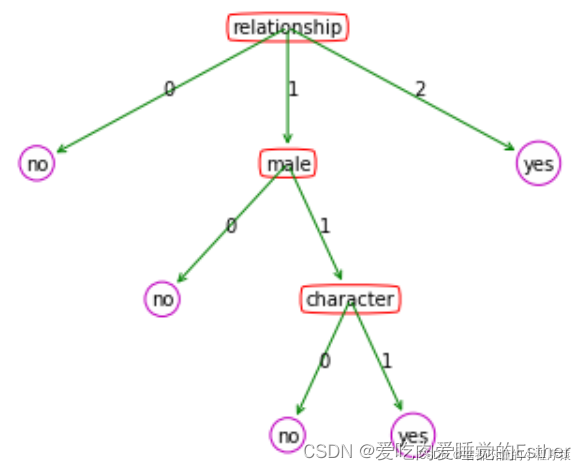
决策树是一种非常经典的机器学习算法，通俗理解的话我们可以举一个例子，比如现在别人要找你借钱，那么按照首先是不是要判断你和他的关系如何?如果关系不好，我就直接拒绝他。如果关系很好，我就直接借给他了，那么如果关系一般，我要判断一下他是男是女？如果是男生，那么就不借，如果是女生，我要继续考虑她的人品好不好？如果人品不好，就不借，如果人品不错，就借。这也就是所谓的决策树。用python画出决策树的图，可以看到相当的直观。也可以说是一个决策的依据。
在这里插入图片描述

1.2 理论分析

决策树（decision tree）是一种常用的机器学习算法，是一种描述对实例进行分类的树形结构。而之前的一个决策树构造，我们往往是根据“经验”来进行构造的，而这些“经验都是来自于我们平时的获取数据”。因此决策树的合理构造也需要数据。
为了便于理解，我们介绍下一个实际的例子。借贷公司根据借贷人是否有房子，是否有工作来决定是否给借贷人发放贷款。
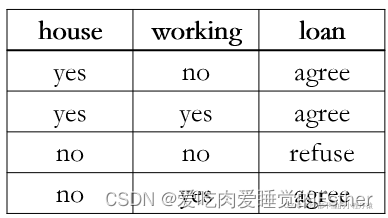
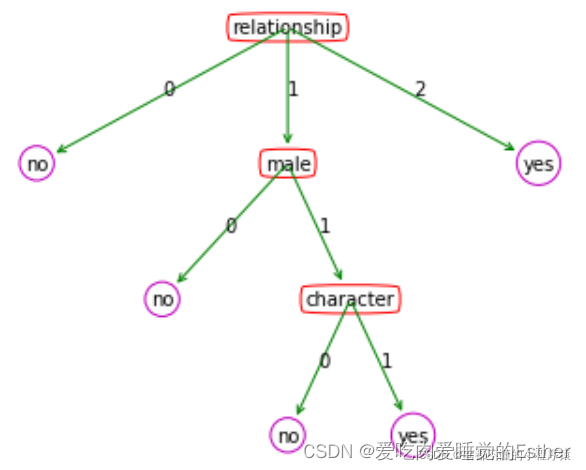
在这里插入图片描述
如下图所示是我们根据数据构造的决策树，你或许会有很多问题，比如我是先判断他是否有房子，还是先判断他是否有工作呢？这也是要构造决策树需要解决的问题。
决策树属于是基于“树”结构来进行决策。
这个树的内部节点也就是方形的内容代表数据集的属性，也就是借钱人的性别啊，关系啊，人品啊，而分支呢？就是属性的取值，也就是性别是男还是女。而最后的叶子节点（通俗来说就是树向下最后一个节点），就是yes和no。这就是一个决策时包含的内容。
在这里插入图片描述

1.3 构造方法

1.3.1 这“棵树怎么长”？

读了上面的内容你就认为你学会了决策树吗？这还仅仅理论内容，实际的代码实现需要算法的思想。因为涉及到树，所以递归属于最核心的算法，构造决策树的策略“分而治之”，决策树的构造是实际上是自根至叶的递归过程。更通俗来说就是说这“棵树怎么长”？
（1）选择一个最优的属性，根据属性值划分成若干个子集；
（2）在每个子集继续构造决策树。

1.3.2 这棵树长到什么时候停？

其中有三种情形导致递归返回，也就是说这棵树长到什么时候停？
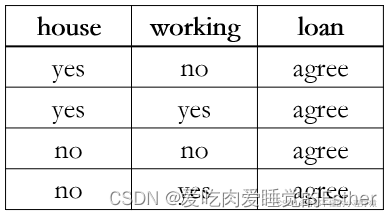
（1）当前节点包含的样本全属于同一类别，无需划分；（比如给出的数据都是同意贷款，那么决策树就是一个agree，无需划分。）
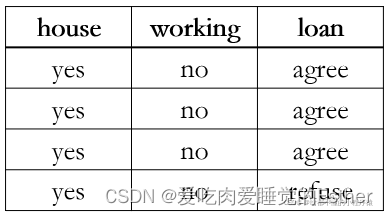
在这里插入图片描述
（2）当前属性集为空，或是所有样本在所有属性上的取值都相同，无法划分。（给出的数据都是有房子，没工作，无法根据属性值划分，递归返回）

（3）当前结点包含的样本集合为空，不能划分。（很容易理解，空的递归返回）

1.4 属性划分选择

其实构造决策树的关键是如何选择最优划分属性。一般而言，随着划分过程的不断进行，我们希望划分后可以分出更多的结果，也就是节点的纯度越来越高。
常用的划分准则有
（1）ID3:信息增益，
（2）C4.5:增益率，
（3）CART：基尼指数。
要说清楚这些问题，我们不得不说一下信息熵的概念。

1.4.1 信息熵

信息奠基人香农（Shannon）认为“信息是用来消除随机不确定性的东西”，也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
“太阳从东边升起”，这条信息并没有减少不确定性，因为太阳肯定是从东边升起的，这是一句废话，信息量为0。”
2018中国队成功进入世界杯“从直觉上来看，这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大，而这句话消除了进入世界杯的不确定性，所以按照定义，这句话的信息量很大。
根据上述可总结如下：信息量的大小与信息发生的概率成反比。概率越大，信息量越小。概率越小，信息量越大。

1.4.2 信息量的计算

设某一事件发生的概率为P(x)，其信息量表示为：
在这里插入图片描述
其中I ( x )表示信息量，这里log表示以e为底的自然对数。就是高中学的lnx。
3.2 信息熵
信息熵也被称为熵，用来表示所有信息量的期望。
期望是试验中每次可能结果的概率乘以其结果的总和。（可以理解最可能获得的结果）
所以信息量的熵可表示为：（这里的X是一个离散型随机变量）
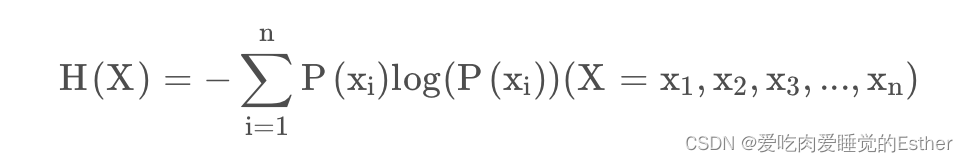
在这里插入图片描述
对于0-1分布的问题，由于其结果只用两种情况，是或不是，设某一件事情发生的概率为，则另一件事情发生的概率为，所以对于0-1分布的问题，计算熵的公式可以简化如下：

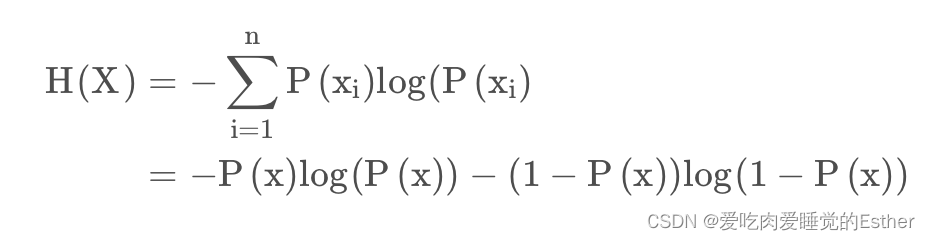
可以总结，信息熵来说，信息熵越大，那么这个事件X发生的不确定性越大，信息熵越小，这个事件X发生的不确定性越小。例如：事件X发生的概率为1，那么事件X不发生的概率为0.这样带入公式计算，H（X）=0，即代表事件X一定发生，也即不确定性为0。
可以看到信息熵最大的特点就是两个概率一样。信息增益越多说明该特征越重要，回到决策树的话题，我们就是根据信息增益来选择特征构造决策树的，这也是这颗决策树怎么长的解决办法。

1.5 划分准则

1.5.1 ID3:信息增益

信息增益：在划分数据集之前之后信息发生的变化。按照属性的特征值划分数据集，计算信息增益，获得信息增益最高的属性就是最好的选择。
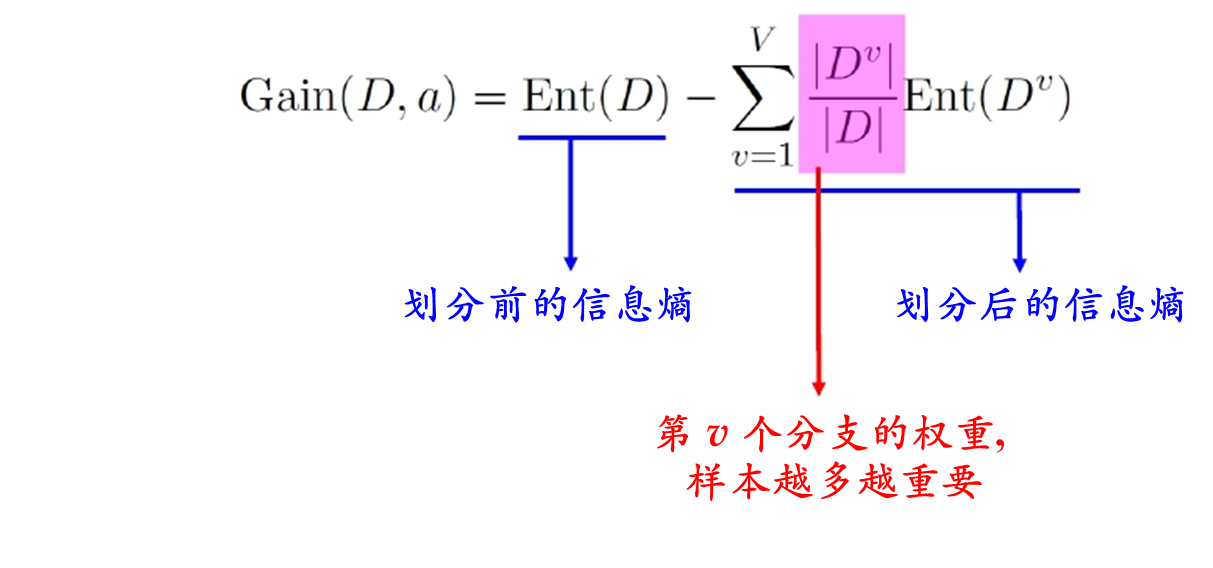
在这里插入图片描述
根据这个准则，需要计算通过不同特征划分后的信息增益率，选择最大值划分数据集，进而构造决策树。信息增益：对可取值数目较多的属性有所偏好，有明显弱点，例如：考虑将“编号”作为一个属性.为了便于读者理解，附上一个例子。
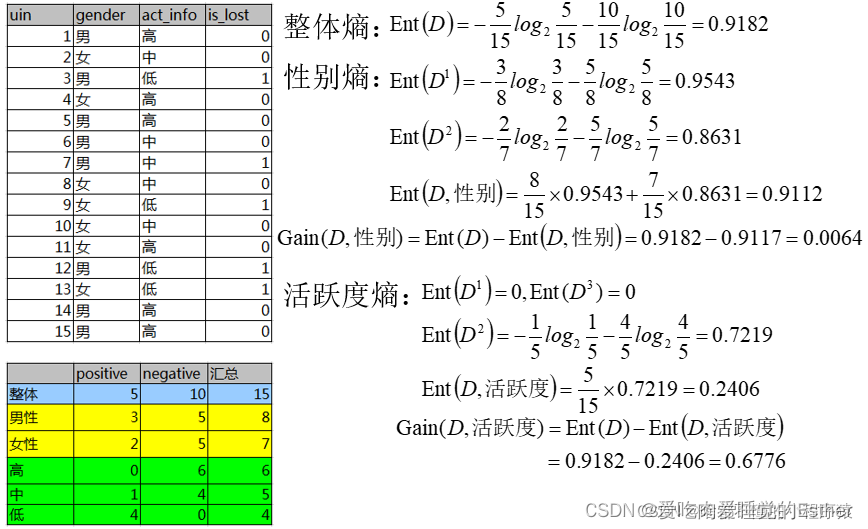
在这里插入图片描述

1.5.2 C4.5:增益率

刚才说到，ID3算法通过信息增益构造决策树，有明显弱点，例如：考虑将“编号”作为一个属性，为了对这一问题改进，产生了C4.5算法，他的划分标准是根据信息增益率划分。
在这里插入图片描述
属性a的可能取值数目越多(即V越大)，则IV(a)的值通常就越大。信息增益比本质：是在信息增益的基础之上乘上一个惩罚参数。特征个数较多时，惩罚参数较小；特征个数较少时，惩罚参数较大。不过有一个缺点：信息增益率偏向取值较少的特征。为了便于读者理解，举个例子。
在这里插入图片描述
使用信息增益率：基于以上缺点，并不是直接选择信息增益率最大的特征，而是现在候选特征中找出信息增益高于平均水平的特征，然后在这些特征中再选择信息增益率最高的特征。

1.5.3 CART:基尼指数

数学家们想到了另外一个表示纯度的方法，叫做基尼指数。表达式如下：
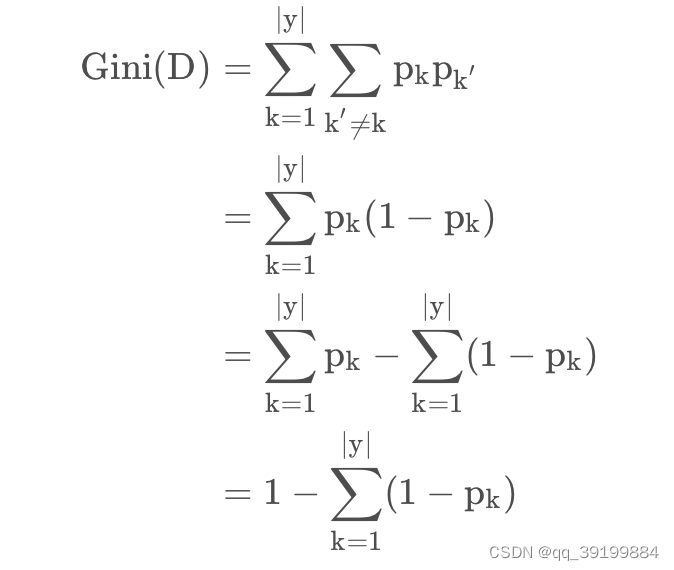
在这里插入图片描述
基尼指数表示在样本集合中一个随机选中的样本被分错的概率。举例来说，现在一个袋子里有3种颜色的球若干个，伸手进去掏出2个球，颜色不一样的概率，这下明白了吧。Gini(D)越小，数据集D的纯度越高。
属性 a 的基尼指数：
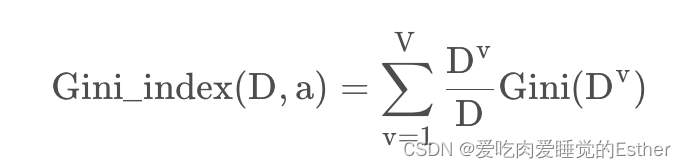
在这里插入图片描述

在候选属性集合中，选取那个使划分后基尼指数最小的属性。

1.6 树形结构为什么不需要归一化?

因为数值缩放不影响分裂点位置，对树模型的结构不造成影响。
按照特征值进行排序的，排序的顺序不变，那么所属的分支以及分裂点就不会有不同。而且，树模型是不能进行梯度下降的，因为构建树模型（回归树）寻找最优点时是通过寻找最优分裂点完成的，因此树模型是阶跃的，阶跃点是不可导的，并且求导没意义，也就不需要归一化。

既然树形结构（如决策树、RF）不需要归一化，那为何非树形结构比如Adaboost、SVM、LR、Knn、KMeans之类则需要归一化。

对于线性模型，特征值差别很大时，运用梯度下降的时候，损失等高线是椭圆形，需要进行多次迭代才能到达最优点。但是如果进行了归一化，那么等高线就是圆形的，促使SGD往原点迭代，从而导致需要的迭代次数较少。

1.7 决策树如何剪枝

决策树的剪枝基本策略有预剪枝 (Pre-Pruning) 和后剪枝 (Post-Pruning)。

预剪枝:其中的核心思想就是，在每一次实际对结点进行进一步划分之前，先采用验证集的数据来验证如果划分是否能提高划分的准确性。如果不能，就把结点标记为叶结点并退出进一步划分；如果可以就继续递归生成节点。
后剪枝:后剪枝则是先从训练集生成一颗完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来泛化性能提升，则将该子树替换为叶结点。
两种方法的对比:
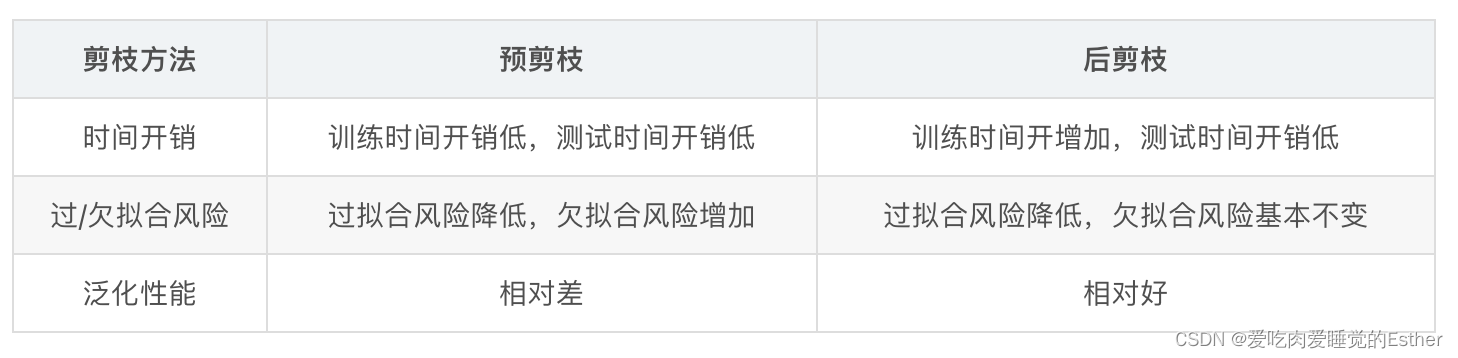
在这里插入图片描述

1.8 Bagging 与随机森林

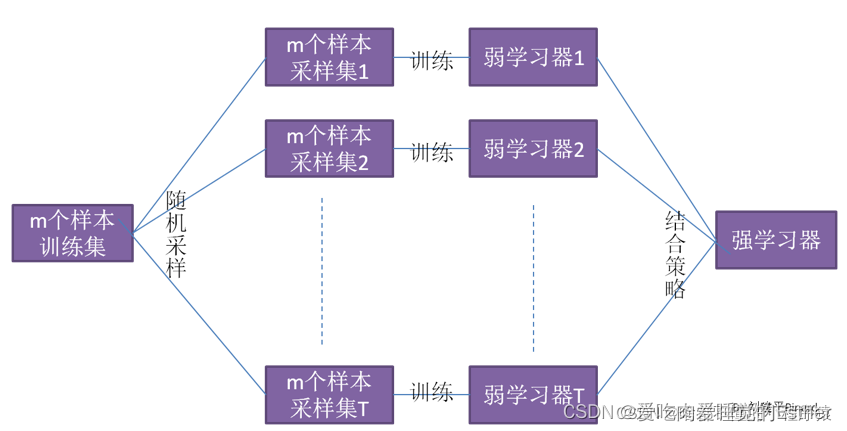
随机森林一句话来说就是三个臭皮匠顶个诸葛亮，人多力量大，也就是说一颗树解决不了问题，那就一堆，大家都发表意见，最终取最多的。这也是随机森林的基本思想。

随机森林：以决策树作为基学习器，同时引入了随机属性选择。即先从属性集合(假定有d个属性)中随机选择一个包含k个属性的子集,再从这个子集中选择一个最优属性进行划分.
（1）当k=d时,基决策树与传统决策树相同.
（2）当k=1时,则随机选择一个属性用于划分.
一般推荐k=log2d.
在这里插入图片描述

二、代码实现

为了降低读者的门槛，这里仅附上调用sklearn的代码。详细代码小程序员将放在百度网盘，供大家参考。
下面是ex4.csv的内容，大家可以新建一个记事本，拷贝下面内容，然后更改文件后缀名为csv.复现代码。

0,0,0,0,0,0,0
1,0,1,0,0,0,0
1,0,0,0,0,0,0
0,0,1,0,0,0,0
2,0,0,0,0,0,0
0,1,0,0,1,1,0
1,1,0,1,1,1,0
1,1,0,0,1,0,0
1,1,1,1,1,0,1
0,2,2,0,2,1,1
2,2,2,2,2,0,1
2,0,0,2,2,1,1
0,1,0,1,0,0,1
2,1,1,1,0,0,1
1,1,0,0,1,1,1
2,0,0,2,2,0,1
0,0,1,1,1,0,1

训练决策树

from pandas import read_csv
df = read_csv("ex4.csv",header=None)
data = df.values
X = data[:,:-1]
y = data[:,-1]
names_chinese = ['色泽','根蒂','敲声','纹理','脐部','触感']
names_english = ['color','root','sound','texture','navel','feeling']
label_chinese = ['好瓜','坏瓜']
label_english = ['good','bad']
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(criterion='entropy')
#model = DecisionTreeClassifier(criterion='entropy',max_depth=3)
#model = DecisionTreeClassifier(criterion='entropy',min_samples_leaf=3)
#model = DecisionTreeClassifier(criterion='entropy',min_samples_split=3)
model.fit(X,y)

决策树可视化
这里可视化需要安装graphviz，报错的可以参考这里

from sklearn.externals.six import StringIO
from sklearn.tree import export_graphviz
from pydotplus import graph_from_dot_data
from IPython.display import Image


dot_data = StringIO()
export_graphviz(model,out_file=dot_data,
               feature_names=['color','root','sound','texture','navel','feeling'],\
               class_names=['good','bad'])
graph = graph_from_dot_data(dot_data.getvalue())
Image(graph.create_png()) #在jupyter中直接显示
#graph.write_pdf("tree.pdf")

结果
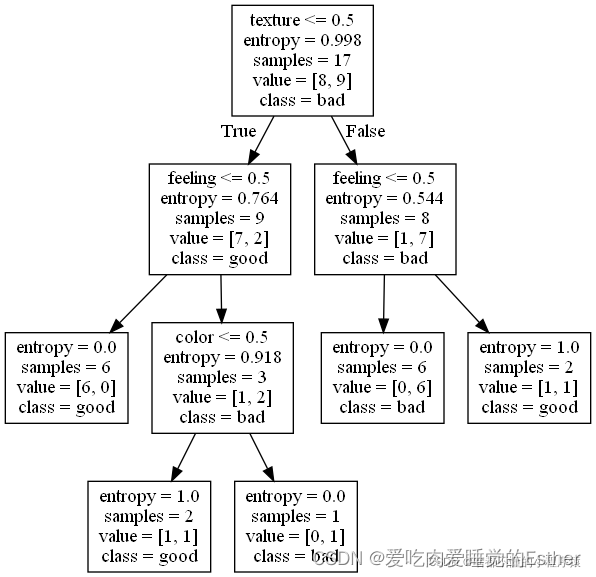
在这里插入图片描述

三、代码文件

小程序员将代码文件和相关素材整理到了百度网盘里，因为文件大小基本不大，大家也不用担心限速问题。后期小程序员有能力的话，将在gitee或者github上上传相关素材。
链接：https://pan.baidu.com/s/1Ce14ZQYEYWJxhpNEP1ERhg?pwd=7mvf
提取码：7mvf