404.左叶子之和

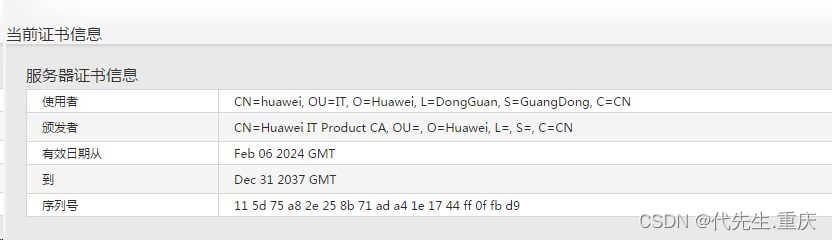
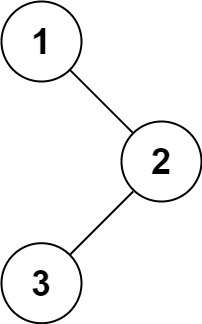
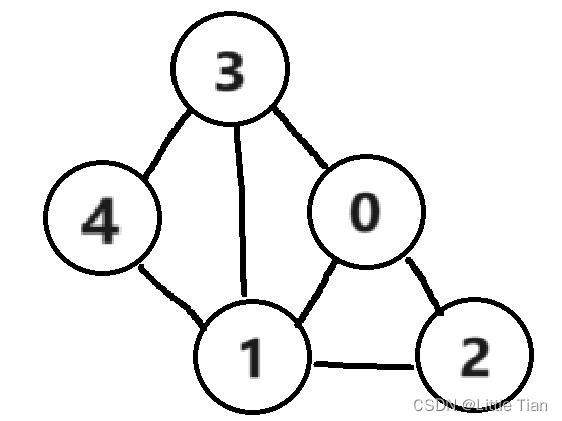
1、这道题需要统计出所有左叶子结点的值的和，首先要明确左叶子节点指的左右孩子节点均为null的左节点。如上图就是4和6.
2.但是光凭叶子结点本身是无法判定左叶子的，因为左右孩子都是null，所以要从上一层节点往下判定。所以判断左叶子的条件语句应该是 root.left != null && root.left.leftnull && root.left.rightnull
3.另外，这道题目采用后序遍历是最方便的。并且要明确递归三要素：返回值、终止条件、递归逻辑。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return getSum(root);
    }
    public int getSum(TreeNode root){
        //终止条件
        if(root == null) return 0;
        if(root.left == null && root.right==null) return 0;
        //递归逻辑
        //左
        int leftSum = getSum(root.left);
        //左子树的条件
        if(root.left != null && root.left.left == null && root.left.right == null) leftSum += root.left.val;
        //右
        int rightSum = getSum(root.right);
        //中
        int sum = leftSum + rightSum;
        return sum;

    }
}

110.平衡二叉树

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return getDepth(root)==-1?false:true;
    }
    //三要素：1、返回值 2、终止条件 3、递归逻辑
    //如果不为平衡二叉树，返回-1
    public int getDepth(TreeNode root){
        if(root == null) return 0;
        int leftHeight = getDepth(root.left);
        if(leftHeight == -1) return -1;
        int rightHeight = getDepth(root.right);
        if(rightHeight == -1) return -1;
        if(Math.abs(leftHeight-rightHeight) > 1) return -1;
        else return Math.max(leftHeight,rightHeight)+1;
    }
}

222.完全二叉树的节点个数

这道题利用了递归和回溯的思想，进入到左子树的递归体对path完成相应的操作之后，在回到主函数中需要将操作的那个值再删除，再进入右子树的递归体。而一旦遇到叶子结点，就是收获结果的时候，要将这个结果加入到res中。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        ArrayList<String> res = new ArrayList<String>();
        ArrayList<Integer> path = new ArrayList<Integer>();//用列表存需要回溯的值
        buildPaths(root,path,res);
        return res;
    }
    public void buildPaths(TreeNode root,List<Integer> path,List<String> res){
        //中，这样避免遗漏叶子结点
        path.add(root.val);
        if(root.left == null && root.right == null){
            //如果左右节点都为空此时要将path中的值转为String放入res中
            res.add(pathToString(path));
            return;
        }
        //左
        if(root.left != null){
            buildPaths(root.left,path,res);
            int len = path.size();
            path.remove(len-1);
        }
        //右
        if(root.right != null){
            buildPaths(root.right,path,res);
            int len = path.size();
            path.remove(len-1);
        }
    }
    public String pathToString(List<Integer> path){
        int size = path.size();
        StringBuilder str = new StringBuilder();
        for(int i = 0;i < size-1;i++){
            str.append(path.get(i)+"->");
        }
        str.append(path.get(size-1));
        return str.toString();
    }
}