图的创建        

        图是一种用于表示对象及其关系的抽象数据结构，由节点（也称为顶点）和连接节点的边组成。图可以分为有向图（Directed Graph）和无向图（Undirected Graph），以及加权图（Weighted Graph）和非加权图（Unweighted Graph）。

本文以无向图为例，用邻接矩阵法来进行图的构建。

邻接矩阵（Adjacency Matrix）:

        1.一个二维数组，用于表示节点之间的连接关系。这里 1 表示相连，0 表示不相连。
        2.如果节点 i 和节点 j 之间有边，则 matrix[i][j] 为 1（有向图）或 matrix[i][j] 和 matrix[j][i] 为 1（无向图）。

下面是一个图的例子：

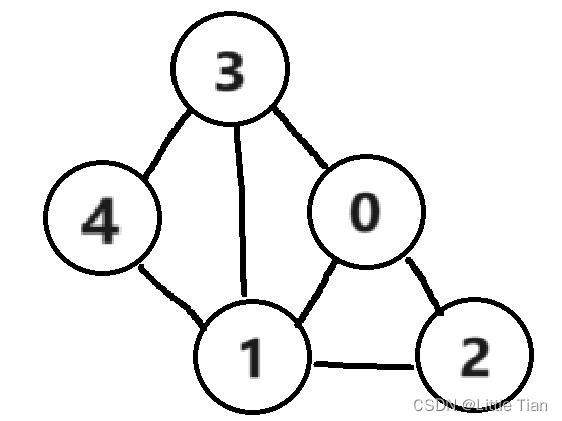
首先我们来定义图结构体：

typedef struct Graph {
	char* vexs; //顶边的标签
	int** arcs; //顶点
	int vexsNum; //标签个数，也可以理解为顶点数
	int arcsNum; //边的个数
}Graph;

        这里vexs是字符串类型是char*，arcs是二级指针模拟二维数组，vexsNum是顶点个数，arcsNum是边的个数。

接着是创建图，为图开辟空间：

Graph* Graph_Init(int num) {
	Graph* G = (Graph*)malloc(sizeof(Graph));
	G->vexs = (char*)malloc(sizeof(char) * num);
	G->arcs = (int**)malloc(sizeof(int*) * num);
	for (int i = 0; i < num; i++) {
		(G->arcs)[i] = (int*)malloc(sizeof(int) * num);
	}
	G->vexsNum = num;
	G->arcsNum = 0;
	return G;
}

        为二级指针开辟vexsNum个一级指针，再为一级指针开辟vexsNum个int空间，这就是二级指针模拟二维数组。如果arcs[i][j]不为0，那么就边数+1，因为加了2遍，所以最后除以2。

void Graph_creat(Graph* G,char* vexs,int* data_vexs) {
	for (int i = 0; i < G->vexsNum; i++) {
		G->vexs[i] = vexs[i];
		for (int j = 0; j < G->vexsNum; j++) {
			G->arcs[i][j] = *(data_vexs + i * G->vexsNum + j);
			if (G->arcs[i][j] == 0) {
				G->arcsNum++;
			}
		}
	}
	G->arcsNum=G->arcsNum/2;
}

接下来就是BFS和DFS遍历：

广度优先搜索 (BFS)

        BFS 算法是从图的一个起始节点开始，探索所有邻居节点，然后逐层向外扩展。通常使用队列数据结构来实现。（类似于树的层级遍历，相当于广撒网）

我们可以写出一个类似于这样的代码：

void BFS(Graph* G,Queue* Q,int*visited,int index) {
    入队第一个顶点
	while (队列不为空)
	{
        出队取得顶点，并且打印顶点。
		for (int i = 0; i < G->vexsNum; i++) {
            //for循环寻找该顶点的相连顶点
			if (如果该顶点与另外一个顶点有联系 && 另外一个顶点没被访问过) {
                入队另外一个顶点
			}
		}
	}
}

        现在的主要问题是如何确定这个元素是否被访问过，我们需要标记访问过的元素。
        我们可以用一个数组来标记，例如如果访问过第二个元素，那么数组对应的位置array[1]就标记为1，其余仍然为0。在每次入队之后置为1，这样会避免多次入队多次访问。 

创建队列的函数就不再写了，最终代码如下：

void BFS(Graph* G,Queue* Q,int*visited,int index) {
	enQueue(Q, index);
	visited[index] = 1;
	while (!Isempty(Q))
	{
		index = deQueue(Q);
		printf("%c ", G->vexs[index]);
		for (int i = 0; i < G->vexsNum; i++) {
			if (G->arcs[index][i] == 1 && visited[i] != 1) {
				enQueue(Q, i);
				visited[i] = 1;
			}
		}
	}
}

深度优先搜索 (DFS)

        DFS 算法是从图的一个起始节点开始，沿着一个路径尽可能深入，然后回溯并探索其他路径。通常使用栈数据结构（递归调用栈或显式栈）来实现。这里用递归实现（相当于一条路走到黑，没路了再回去走其他路）。

我们可以先写出类似这样的代码：

void DFS(Graph* G, int* visited, int index) {
    接收访问顶点并且标记已访问
	for (int i = 0; i < G->vexsNum; i++) {
        //for循环寻找顶点的相连顶点
		if (如果和其他顶点有联系 && 其他顶点未访问) {
			DFS(G, visited, i);//递归其他顶点
		}
	}
}

最后我们可以写出下面的代码：

void DFS(Graph* G, int* visited, int index) {
	printf("%c", G->vexs[index]);
	visited[index] = 1;
	for (int i = 0; i < G->vexsNum; i++) {
		if (G->arcs[index][i] == 1 && visited[i] == 0) {
			DFS(G, visited, i);
		}
	}
}

这就是文章的全部内容了，希望对你有所帮助，如有错误欢迎指出。