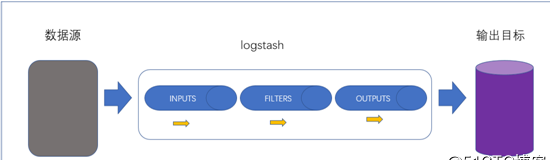
目录
一、无向图割点、桥、双连通分量
Tarjan 算法求割点和桥(割边)
“割点”代码
边双和点双连通分量
边双连通分量 和 点双连通分量 的缩点
二、有向图强连通分量
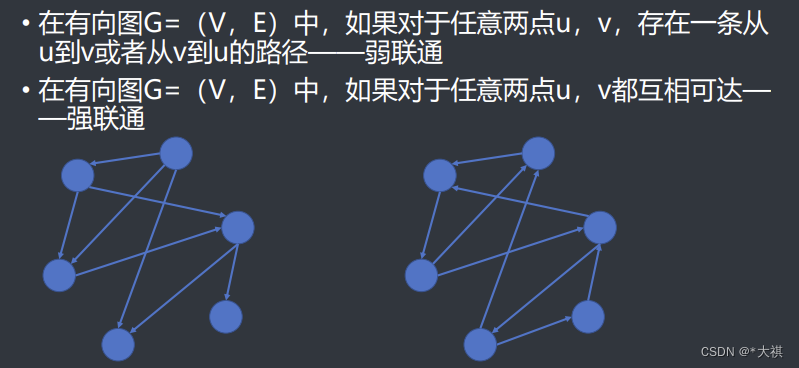
1.有向图的弱连通与强连通
2.强连通分量
Kosaraju算法
Tarjan 算法(求强连通分量)
一、无向图割点、桥、双连通分量
- 给定无向连通图 G = (V, E)
- 对于一个点 x,若从图中删除 x 及所有与 x 相连的边,图不再连通,x 是 G 的割点
- 对于一条边 e,从图中删去 e,图不再连通, e 是 G 的割边
- 一个图如果不存在割点,则它是一个点双连通图,一个图的极大点双连通子图是它的点双连通分量。
- 一个图如果不存在割边,则它是一个边双连通图,一个图的极大边双连通子图是它的边双连通分量。
先借用OI Wiki (传送门)的图解释几种边:

Tarjan 算法求割点和桥(割边)
- 时间戳 dfn:第几个搜到这个点
- 返祖边:搜索树上一个点连向它另一条支链上的点的边
- (横插边:在搜索树上一个点连向它另一条支链上的点的边——在无向图中不存在【因为下一条支链在dfs序中会直接接在当前这条支链后面成为“子树”】
- 追溯值 low:当前点及其子树通过一条返祖边能连到的最小 dfn 值
- 如果 <u, v> 是搜索树的边:low[u] = min(low[u], low[v])
- 如果 <u, v> 是返祖边:low[u] = min(low[u], dfn(v))
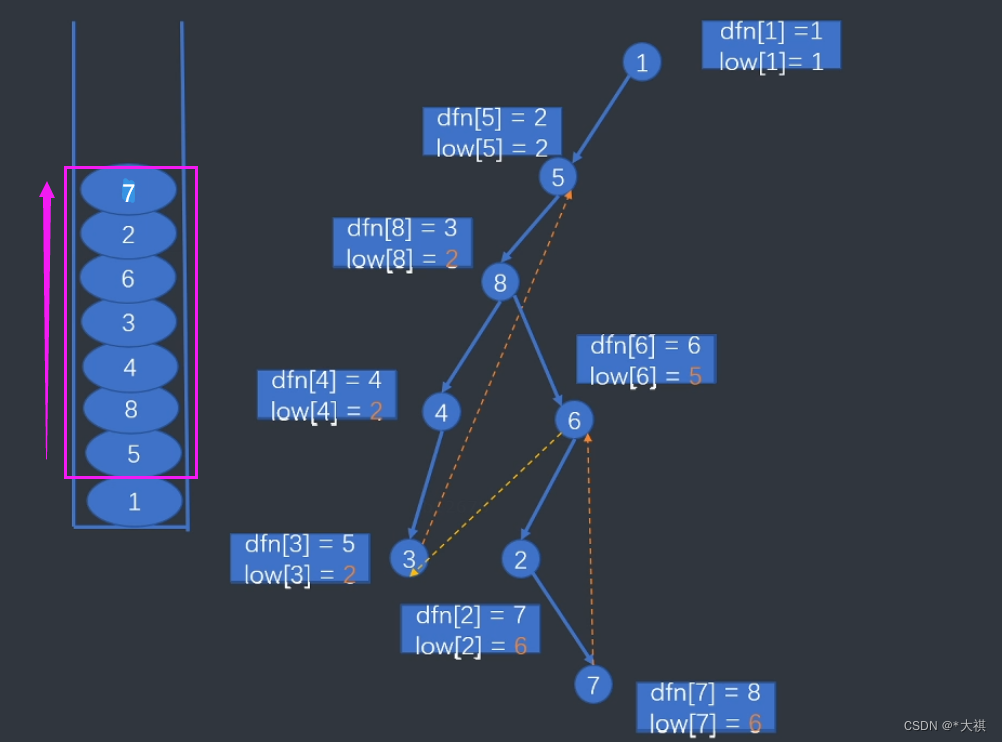
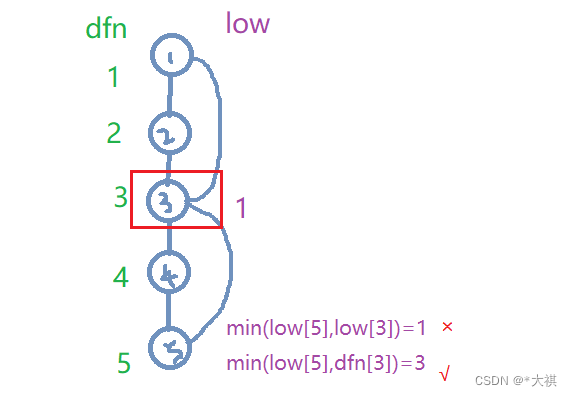
下面来看一个连通图,寻找割点和割边(桥)所满足的规律。右图为左图的一个dfs搜索树,水蓝色标记每个点的dfn(时间戳),梅红色标记每个点的 low 值。

low 值宜从叶节点开始标记,因为其值作为子节点可以向上更新父节点的 low 值,比如序号为4的点有一条连向1号节点的返祖边,其 low 值为1,7号结点 low 值等于其 dfn = 9,10号结点 low 值也为8,而对于8号结点,它的子树中4号结点 low 值为1,根据 “ 如果 <u, v> 是搜索树的边:low[u] = min(low[u], low[v]) ” ,其 low 值为1 ,再依次向上更新。
例如:10号点为割点,若将其去掉,其下的7号结点无法与上面的连通。
规律:【割点有两类】:
- 子树里不存在跨越它连向它上方的点的边
- 有多个儿子的根
(u, v)割边(u 为父亲,v 为儿子):以 v 为根的子树中不存在连向 u 以及 u 上方的边。
用low和dfn的关系表示即
- u点是割点, v 是 u 搜索树上的一个儿子:① dfn[u] <= low[v] —— v的子树中没有返祖边能跨越 u 点;② 有多个儿子的根节点
- 边是桥,搜索树上 v 是 u 的一个儿子:dfn[u] < low[v] —— v 的子树中没有返祖边能跨越<u,v> 这条边
注意割点的式子有等号,判割边的没有等号(如果有一条返祖边将 v 与 u 相连,则dfn[u] = low[v] ,这时原本v和u相连的边删掉也能连通,故u-v不是割边)
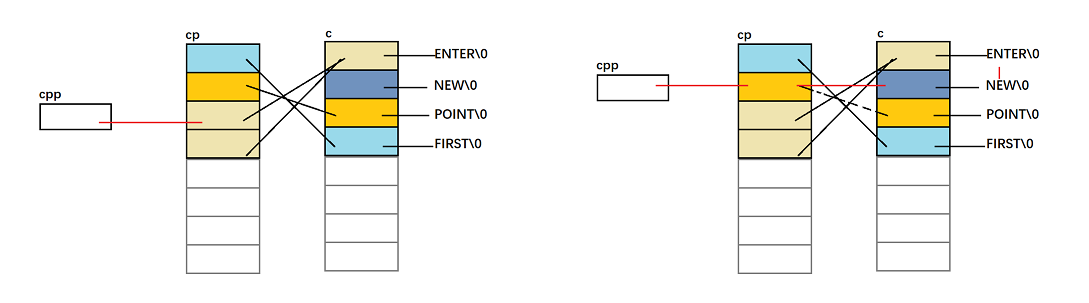
“割点”代码
注意第32行为 dfn[y],与第25行的 low[y] 不一样。在求“割边”里写成 low[y] 虽然也不会错,但在求割点里就是错的,可能有些题目数据不够强这里写错了也能过,但一旦错了就很难找到,所以极度建议割点割边代码此处按照定义写成一致,能大大减少出错率。

关于为什么写low[y]为错的说明:
如下图,因为搜索的顺序不确定(取决于建图时的顺序)若3号点的low值通过一条返祖边更新为1后,再来更新5号结点时,若是 low[x] = min(low[x],low[y]),low[5]=low[3]=1,然后4号点就会继承5号点的 low 值也为1,这样dfn[3]>=low[4],就会误判点3不是割点,而事实上3号点是割点。这里相当于是将1--3这条返祖边与3--5这条返祖边连起来当成了1--5的返祖边,而我们的low值定义是当前点及其子树通过一条返祖边能连到的 最小dfn 值。5到3,3再到1,而3恰是我们的割点,而求割边的时候就不会出现这种情况,跨越了一条边就是跨越了一条边,不会存在要两条边连在一起才跨越一条边。
边双和点双连通分量
- 把桥删了每个连通块都是一个边双连通分量——标记处桥之后dfs一遍即可
- 点双连通分量要复杂一些——一个割点可能属于多个双连通分量
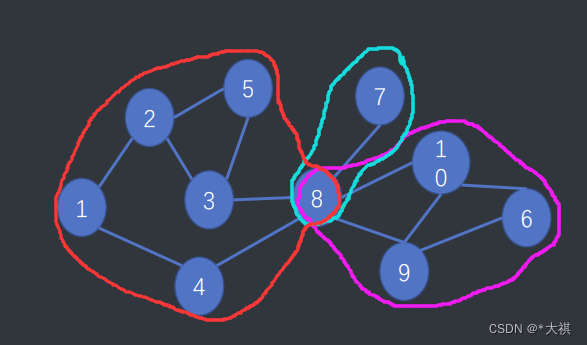
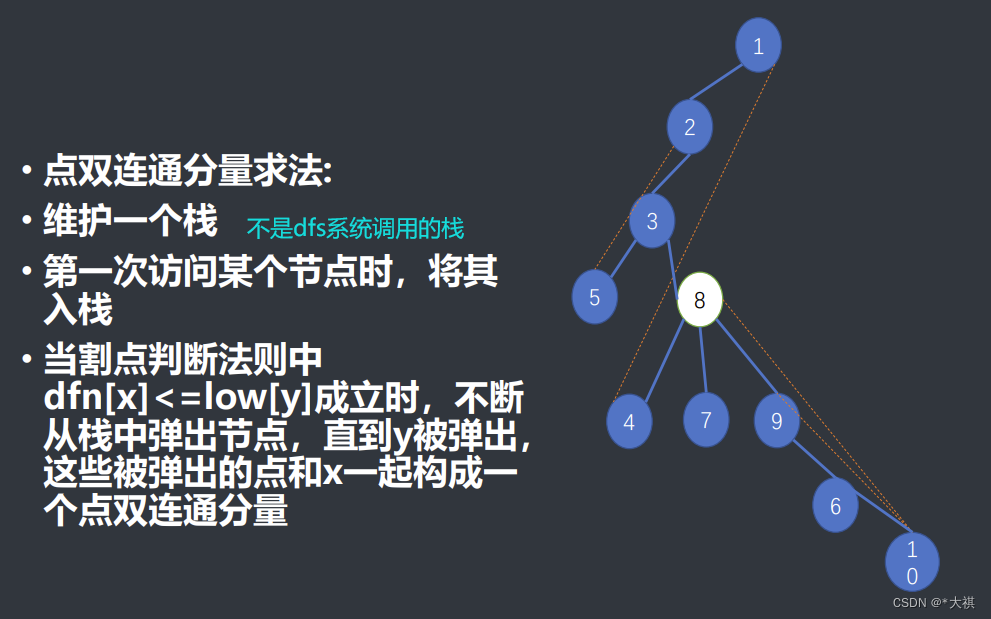
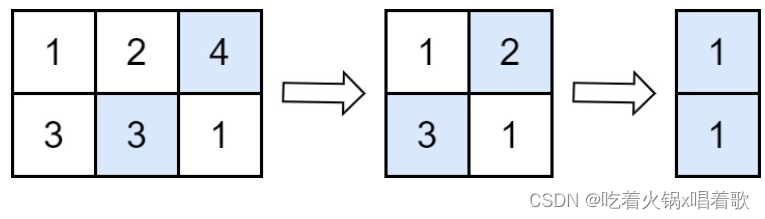
dfs时(这里假设在8号结点先搜向9的那条支链)……9入栈,6入栈,10入栈,再向上返回(系统dfs递归调用的返回,系统栈的10,6,9弹出,自己维护的栈没有弹出)当返回到结点8时,dfn[8] <= low[y],判断8为割点,此时弹出自己维护的栈里8以上的所有结点(10,6,9)与8组成一个点双连通分量;8再到7号结点,发现7号结点没有儿子结点了,再返回,又成立dfn[8]<=low[7],8为割点,于是弹出7号点与8组成第二个点双连通分量;8再到4,发现low[4]=1,low[4] < dfn[8],8不是其中的割点……到最后回到根节点1,因为所有的结点的low值总不会比根节点的dfn还要小,即只有一个子节点的根节点总是割点,所以靠1号根节点将剩余的所有点弹出,组成最后一个点双连通分量。(无所谓,根节点会出手)
边双连通分量 和 点双连通分量 的缩点
- 每个边双连通分量缩成一个点,再用原来的桥把它们连起来
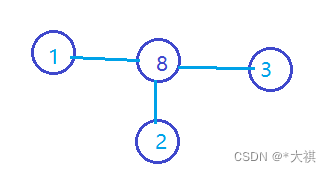
- 点双连通分量因为一个割点可能包含在多个点双连通分量里面,所以我们将每个割点保留割点与其所在的点双连通分量连边即可。
如上图的点双连通分量可改为:
二、有向图强连通分量
1.有向图的弱连通与强连通
2.强连通分量

如上图的黄色点构成一个强连通分量。
Kosaraju算法
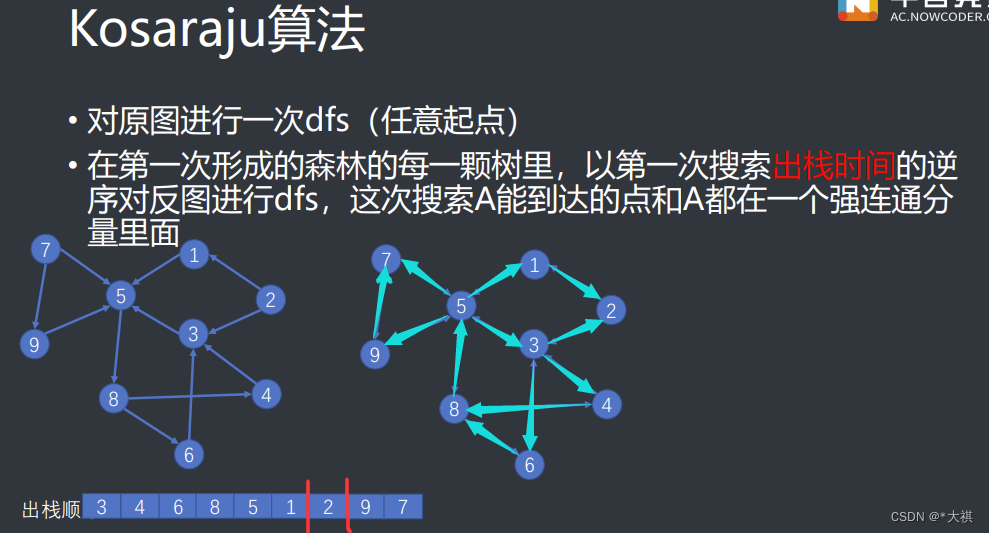
对左图,从1开始搜:1进栈,5进栈,8进栈,4进栈,3进栈,3不能往下搜了,3出栈,回到4,4也没有向下搜的点,4出栈,回到8,6进栈,6出栈,8出栈,5出栈,1出栈;
然后再找图中一个没有访问过的点继续上述操作,从2开始,2入栈,2出栈;
再从7开始,7入栈,9入栈,9出栈,7出栈。
得到出栈顺序:3,4,6,8,5,1,2,9,7
再以这个出栈时间的逆序对反图(即原来A->B变为B->A)进行dfs:从7开始,7无法到达其它点,7独自为一个强连通分量;再看9,因为9原本能去到的7已经被删了,9也单独是一个强连通分量;2号点为一个强连通分量;1号点为一个强连通分量(原本可以通向的2号点已经成为一个单独的强连通分量了);又5->3->4->8,3->6,所以5,3,4,6,8为一个强连通分量
原理:在一个 dfs 搜索树里面,越先出栈说明越多的点可以到达这个点,即在它后面的点都能到达它,如【3,4,6,8,5,1】3后面的点都能到达3,4后面的点都能到达4,依此类推。若顺序为A, B, C, 则实际图中关系为 A<--B<--C,那么倒叙,反图能到(C-->B)也即原图有反向边能到(C<--B)【意会~意会~】
Tarjan 算法(求强连通分量)