332.重新安排行程
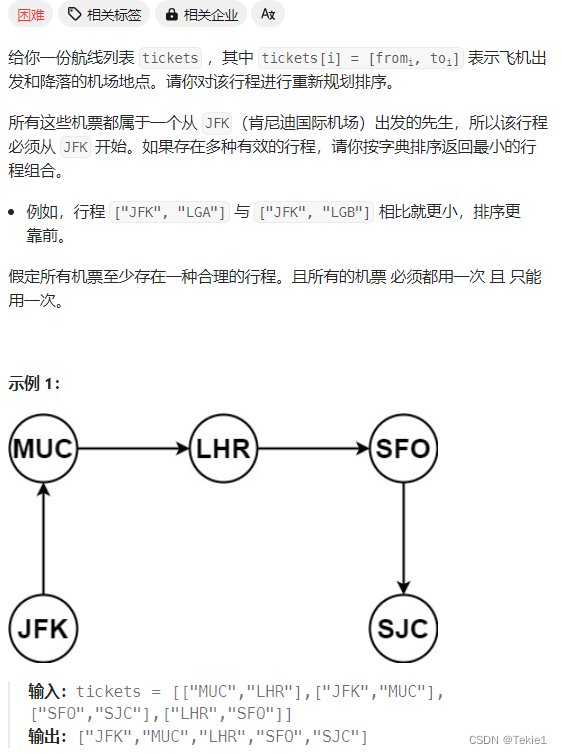
难题,自己写的代码没过,但我认为逻辑没有问题
class Solution {
public:
vector<string> res;
bool pruning(vector<string> res, vector<string> path) {
if (res.size() == 0)
return true;
bool check = false;
for (int i = 0; i < path.size(); i++) {
if (path[i] <= res[i])
check = true;
// 如果是第一次字典序就比res大,那么就可以剪枝
if(path[i] > res[i] && !check)
return false;
}
return true;
}
bool compare(vector<string> res, vector<string> path) {
if (res.size() == 0)
return true;
for(int i = 0;i<res.size(); i++){
if(path[i] == res[i]) continue;
else if(path[i] < res[i]) return true;
else return false;
}
return true;
}
void backTracking(vector<vector<string>>& tickets, vector<bool>& used,
vector<string>& path) {
if (path.size() == tickets.size() + 1) {
if (compare(res, path)) {
res = path;
}
return;
}
for (int i = 0; i < tickets.size(); i++) {
if (used[i])
continue;
if (path[path.size() - 1] != tickets[i][0])
continue;
path.push_back(tickets[i][1]);
if (!pruning(res, path)) {
path.pop_back();
continue;
}
used[i] = true;
backTracking(tickets, used, path);
used[i] = false;
path.pop_back();
}
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
for (int i = 0; i < tickets.size(); i++) {
if (tickets[i][0] != "JFK")
continue;
vector<bool> used(tickets.size(), false);
vector<string> path;
path.push_back(tickets[i][0]);
path.push_back(tickets[i][1]);
used[i] = true;
backTracking(tickets, used, path);
used[i] = false;
}
return res;
}
};
正确的方法应该是使用一个map记录某个点到另一个点的机票数,类似于used数组的作用,但是如果使用map记录,因为map本身是有序的,所以在遍历的时候,第一个满足条件的一定是最小的路径。
终止条件就是字符串数比票数多1的时候。
这里返回值使用bool类型,当找到第一个符合条件的时候,直接返回true就行,然后它会一直返回给上层,直接退出函数,此时res是找到的第一个符合条件的路径,又因为map是自然有序的,所以res内就是答案
class Solution {
public:
unordered_map<string, map<string, int>> targets;
bool backTracking(vector<vector<string>>& tickets, vector<string>& res) {
if (res.size() == tickets.size() + 1) {
return true;
}
// map是有序的,所以先遍历的string字典序小,优先按小路线走
for (auto& target : targets[res[res.size() - 1]]) {
if (target.second > 0) {
res.push_back(target.first);
target.second--;
if (backTracking(tickets, res))
return true;
res.pop_back();
target.second++;
}
}
return false;
}
vector<string> findItinerary(vector<vector<string>>& tickets) {
vector<string> res;
for (int i = 0; i < tickets.size(); i++) {
string first = tickets[i][0];
string second = tickets[i][1];
targets[first][second]++;
}
res.push_back("JFK");
backTracking(tickets, res);
return res;
}
};
51.N皇后

难点在于斜线上的判断
棋盘需要初始化,全为.
代码里是每次遍历一行,其实从左向右遍历每一列放棋子也是可以的
棋盘的宽度就是递归树的宽度,棋盘的高度就是递归树的深度
class Solution {
public:
vector<vector<string>> res;
bool check(int row, int col, vector<string>& board, int n) {
// 检查列
for (int i = 0; i < row; i++) {
if (board[i][col] == 'Q')
return false;
}
// 检查左斜上方
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q')
return false;
}
// 检查右斜上方
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q')
return false;
}
return true;
}
void backTracking(int row, int n, vector<string>& board) {
if (row == n) {
res.push_back(board);
return;
}
for (int i = 0; i < n; i++) {
if (!check(row, i, board, n))
continue;
board[row][i] = 'Q';
backTracking(row + 1, n, board);
board[row][i] = '.';
}
}
vector<vector<string>> solveNQueens(int n) {
vector<string> board(n, string(n, '.'));
backTracking(0, n, board);
return res;
}
};
37.解数独

这道题是需要搜索一种满足条件的情况,无须遍历整个搜索树,所以回溯函数需要提供返回值类型(bool)
该题不需要递归终止条件,因为终止表现在返回值bool里,一旦找到满足条件的就返回true
且该题是一个二维搜索,而不是像之前的n皇后一样一次搜索一层,放一个皇后一样,该题需要直接使用2层for循环进行搜索,然后再使用一层for循环来遍历放的数字
class Solution {
public:
bool check(int row, int col, char k, vector<vector<char>>& board) {
// 1.检测同行
for (int i = 0; i < board[row].size(); i++) {
if (board[row][i] == k)
return false;
}
// 2.检测同列
for (int i = 0; i < board.size(); i++) {
if (board[i][col] == k)
return false;
}
// 寻找该位置属于的3*3宫的左上角的位置
int startrow = (row / 3) * 3;
int startcol = (col / 3) * 3;
for (int i = startrow; i < startrow + 3; i++) {
for (int j = startcol; j < startcol + 3; j++) {
if (board[i][j] == k)
return false;
}
}
return true;
}
bool backTracking(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[i].size(); j++) {
// 如果是数字,则说明是给出的或者已经填好的,跳过即可
if (board[i][j] != '.')
continue;
for (char k = '1'; k <= '9'; k++) {
if (check(i, j, k, board)) {
board[i][j] = k;
if (backTracking(board))
return true;
board[i][j] = '.';
}
}
// 如果遍历了1-9,在该位置都无法获得一个true的答案的话,那么返回false,之后就会在上一层递归进行board的回退
return false;
}
}
return true;
}
void solveSudoku(vector<vector<char>>& board) { backTracking(board); }
};