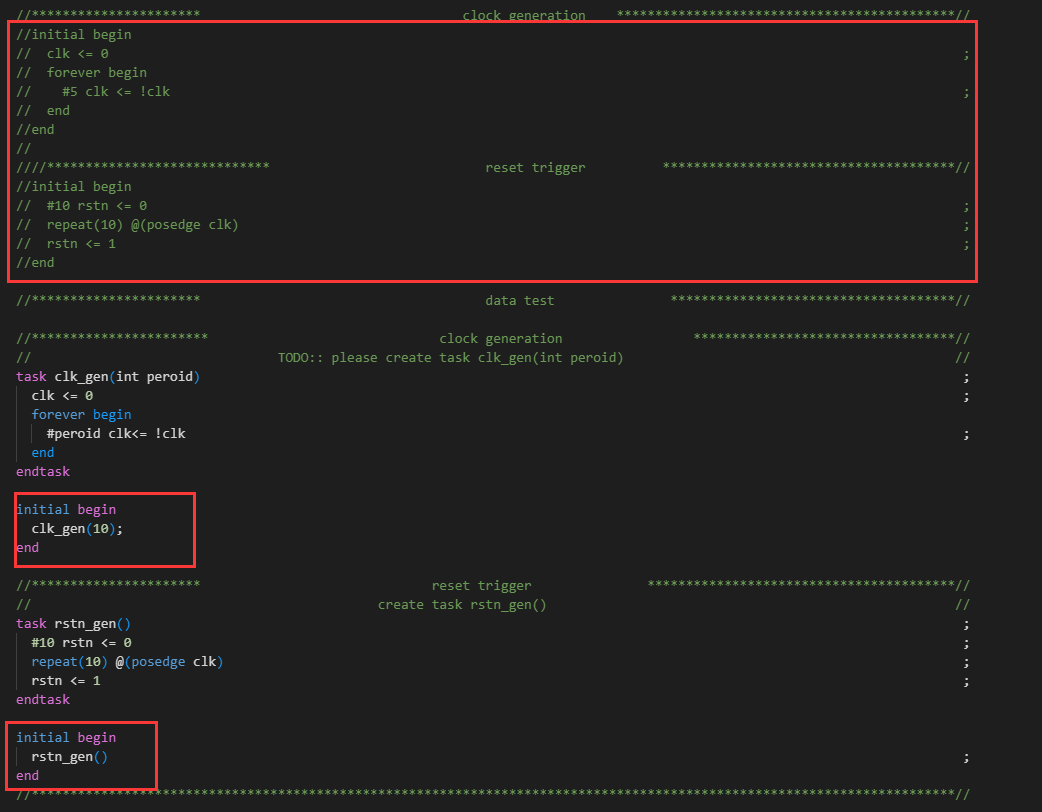
题目链接：18. 四数之和 - 力扣（LeetCode）

普通版本（排序 + 双指针）

主旨：类似于三数之和的解法，但需要多加一些限制，同时为了防止多个数组元素的相加之和出现整型溢出问题还要将整型转为long

补充：(long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] 是表达式的类型提升，有一个long则后面的所有运算均提升为long操作 

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> quadruplets;
        if (nums.size() < 4) {
            return quadruplets;
        }
        sort(nums.begin(), nums.end());
        int length = nums.size();
        for (int i = 0; i < length - 3; i++) 
        {
            if (i > 0 && nums[i] == nums[i - 1]) 
            {
                continue;
            }
            if ((long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) 
            {
                break;
            }

            if ((long) nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) 
            {
                continue;
            }

            for (int j = i + 1; j < length - 2; j++) 
            {
                if (j > i + 1 && nums[j] == nums[j - 1]) 
                {
                    continue;
                }
                if ((long) nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) 
                {
                    break;
                }
                if ((long) nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) 
                {
                    continue;
                }
                int left = j + 1, right = length - 1;
                while (left < right) 
                {
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum == target) 
                    {
                        quadruplets.push_back({nums[i], nums[j], nums[left], nums[right]});
                        while (left < right && nums[left] == nums[left + 1]) 
                        {
                            left++;
                        }
                        left++;
                        while (left < right && nums[right] == nums[right - 1]) 
                        {
                            right--;
                        }
                        right--;
                    } 
                    else if (sum < target) 
                    {
                        left++;
                    } 
                    else 
                    {
                        right--;
                    }
                }
            }
        }
        return quadruplets;
    }
};

时间复杂度：O（N^3）（查找前两个数要两次for，查找后两个数因为有双指针同时向里走的缘故，所以只用一层for）

空间复杂度：O（log n） （仍然是花费在了排序的额外空间上）

优化版本（待补充）

~over~