渐近符号
基本的渐近符号：
O 表示上界，即小于等于 ≤
Ω 表示下界，即大于等于 ≥
Θ 表示渐近等于 =（上一集也有使用这个符号）

还有几个严格符号：
o 表示小于 <
ω 表示大于 >

渐近符号O
主要详细讲解了渐近符号O
对于f(n) = O(g(n))，表示存在适当的常数c>0,n0>0，使得f(n) ≤ c·g(n)，对于所有的n≥n0

f(n)可以说是属于g(n)构成的函数集，可以定义O(g(n))为一个函数集
O(g(n)) = { f(n)：存在c>0、n0>0，使得0≤f(n)≤cg(n)，其中n≥n0 }

严格意义上来讲，f(n) = O(g(n))中的等号=是不对称的
即不能从右边推算到左边。这里表达的意思是属于某个集合
即相当于f(n) ∈ O(g(n))

有一些关于O符号的精妙用法，把它当作宏来用，
例子：f(n) = n3 + O(n2)
表示f(n)主要是n3，但是还有个低阶项O(n2)。即存在某函数h(n)=O(n2)，使得f(n) = n3 + h(n)。O(n2)是一个误差项

例子：n2 + O(n) = O(n2)
表示对所有f(n)∈O(n)，存在h(n)∈O(n2)，使得n2+f(n)=h(n)

渐近符号Ω
f(n) = Ω(g(n)) 这里比较简单带过，Ω的集合版定义为：
Ω(g(n)) = { f(n)：存在c>0、n0>0，使得0≤cg(n)≤f(n)，其中n≥n0 }

渐近符号Θ
Θ(g(n)) = O(g(n)) ∩ Ω(g(n))

解递归式
解递归式没有通用的方法（没有万金油），但是有三种主要的方法：代换法、递归树法、主方法。

代换法
代换法和解积分类似，主要有三个步骤：

1.猜答案，不需要非常精确
2.验证
3.找出常数系数，使问题成立

注：代换法的验证是使用数学归纳法，在这一步不能使用O符号。

一个错误的证明：
要证明n=O(1)【显然是不成立的，不然所有算法都是常数复杂度了】
因为
1 = O(1)
…（逐步归纳）
n-1 = O(1)
所以n = (n-1)+1 = O(1) + O(1) = O(1)

上面的证明是错误的，不能在归纳中使用O，因为这里的常数是变化的。如果是有穷数量的常数加倍，没太大问题，这依然是一个常数。但如果是2k次的这种加倍就有问题了，常数是依赖于n变化的。在归纳过程中，要保证常数系数是不变的。

---

练习一
T(n) = 4T(n/2) + n
T(1) = Θ(1)

猜测①：T(n) = O(n3)
验证：T(k) ≤ c(k3)，其中k<n
验证过程如下：
T(n) = 4T(n/2)+n
… ≤ 4c(n/2)3+n
… = (1/2)cn3+n
… = cn3-[(1/2)cn3-n]
其中，cn3为理想情况，余项=[(1/2)cn3-n]
T(n) ≤ cn3, if 余项=[(1/2)cn3-n]≥0
这里的c是一个常数系数，可以设定任何想要的值。比如设置c=2，猜测成立。

---

1.猜测②：T(n)=O(n2)
2.验证：T(k) ≤ c(k2)，其中k<n
验证过程如下：
T(n) = 4T(n/2)+n
… ≤ 4c(n/2)2+n
… = cn2+n
… = cn2-(-n)
其中，cn2为理想情况，余项=-n
T(n) ≤ cn2, if 余项=-n ≥ 0
因为n≥1，所以显然不成立。

---

1.猜测③：T(n) = O(c1n2-c2n)
2.验证：T(k) ≤ c1k2-c2k，其中k<n
验证过程如下：
T(n) = 4T(n/2)+n
… ≤ 4[c1(n/2)2-c2(n/2)]+n
… = c1n2 - 2c2n + n
… = c1n2 - c2n - (c2n-n)

其中，c1n2为理想情况，余项=c2n-n
so，T(n) ≤ c1n2-c2n，if 余项=c2n-n ≥ 0，即c2≥1。
当n=1，T(1) ≤ c1 - c2，又因为T(1) = Θ(1)，故c1>c2。

---

一般大家都比较关心上界，所以只求O，不过偶尔也会求一下下界Ω。

递归树法
在上一集讲归并排序的时候，讲了一点递归树法。这节课找了个稍微复杂点的例子。

练习二
T(n) = T(n/4) + T(n/2) + n2
… = n2 + T(n/4) +T(n/2)
… = n2 + (n/4)2 + T(n/16) + T(n/8) + (n/2)2 + T(n/8) + T(n/4)
… = n2 + (n/4)2 + (n/2)2 + [(n/16)2] + [(n/8)2] + [(n/8)2] + [(n/4)2]
… = …

---

注：为了简洁书写，表示[(n/8)2]表示T(n/8)的展开形式

用脑图来表示递归树
第一次展开：T(n) = T(n/4) + T(n/2) + n2，如下图：

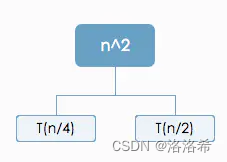
第二次展开：T(n) = n2 + (n/4)2 + T(n/16) + T(n/8) + (n/2)2 + T(n/8) + T(n/4)，如下图：

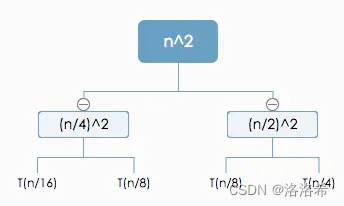
继续展开：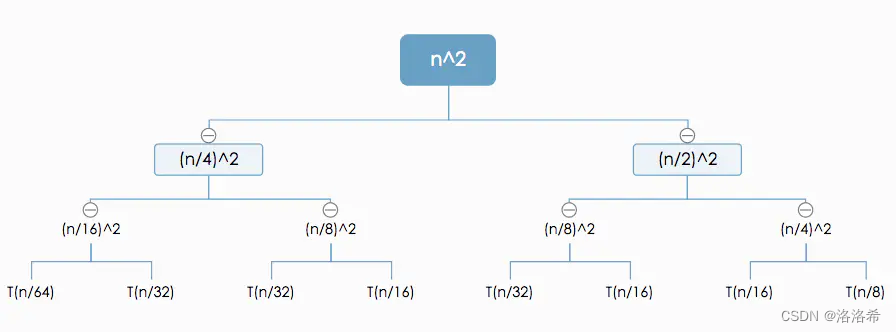
观察得到，算法的初始规模为T(n)，每次递归分解为一个T(n/4)和T(n/2)，每次都会比上一级减少1/4的n，所以可推断最后的叶节点数量 < n

一直递归到T(1)，即常数。观察可得，递归树每层n2的系数是一个等比级数，如第一层为1，第二层为5/16，第三层为25/256…
可得n2的系数总和=1 + 5/16 + 52/162 + … + 5k/16k ≤ 2

也就是T(n) ≤ 2n2 +n = O(n2)

主方法
主方法是递归树法的一个应用，但是比递归树法更精确。但只能应用到特定的递归式上。
特定的递归式：
T(n) = aT(n/b)+f(n)，其中a≥1，b>1，f(n)渐近趋正。
对于规模为n的算法，每次递归可以转化为a个规模为n/b的算法，以及一个非递归的代价f(n)。

渐近趋正：对于足够大的n，f(n)是正的。即存在n0，当n≥n0，f(n)>0。

主方法有个简单的思路：比较非递归函数f(n)和函数nlogba（表示递归树叶节点的数量）的大小，比较的结果有三种情况：小于，等于，大于。

情况一：小于
对于第一种情况，f(n) < nlogba。
即：f(n) = O(nlogba - ε)，ε>0
==> T(n) = Θ(nlogba)，即由nlogba作为主导，忽略f(n)。

情况二：等于
第二种情况，f(n) = nlogba
注意：这里的等于不是完全等于，而是基本等于。
即：f(n) = Θ(nlogba · lgkn)，k≥0
==> T(n) = Θ(nlogba · lgk+1n)，即f(n)·h，h=lgn。

情况三：大于
第三种情况，f(n) > nlogba
即：f(n) = Ω(nlogba + ε)，ε>0
还需要考虑f(n)是如何增长的，需要确保在递归的过程中，f是不断减小的，否则可能得到无限大的值。。
即要求【下一层的总代价af(n/b)】 ≤ 【小于当前层的代价(1-ε’)f(n)】 ，ε’ > 0，(1-ε’)表示严格<1
==> T(n) = Θ(f(n))，即由f(n)作主导，忽略nlogba。

练习三
T(n) = 4T(n/2)+n
代入以上的公式【T(n)=aT(n/b)+f(n)】可得：a=4,b=2,f(n)=n
计算可得nlogba = n2
接下来比较 f(n)=n 和 nlogba=n2
因为n ≤ n2，所以符合第一种情况，故T(n) = Θ(n2)

练习四
T(n) = 4T(n/2)+n2
代入以上的公式【T(n)=aT(n/b)+f(n)】可得：a=4,b=2,f(n)=n2
计算可得nlogba = n2
接下来比较 f(n)=n2 和 nlogba=n2
因为n2 == n2，所以符合第二种情况，故T(n) = Θ(n2lgk+1n)
即T(n) = Θ(n2lgn)，设定k=0

练习五
T(n) = 4T(n/2)+n3
省略一下推算，符合第三种情况
即T(n) = Θ(n3)

为了好复习好找到这个笔记，我就搬运过来了
作者：LuLuX
链接：https://www.jianshu.com/p/867fba3d0220
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。