前缀树 字典树 TrieTree的学习与模拟实现

news2025/4/27 21:34:42

目录

前言

哥们在去年12月的一次实习面试的时候，远在旧金山的一家美企CTO面试我，岗位在西安，只招一个C++实习生，然后和以往面试不同的是，他偏向问算法多一些:这几道题;

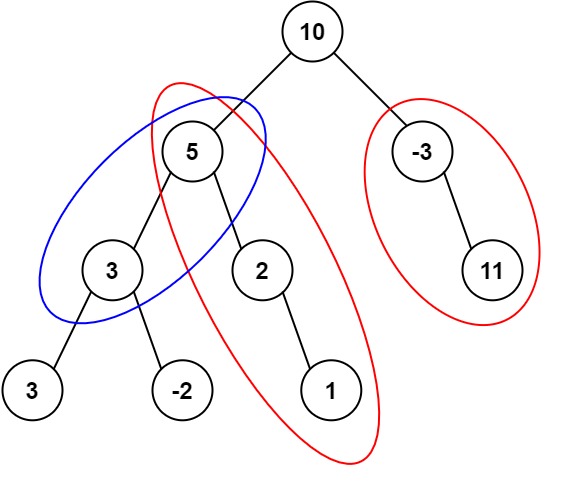
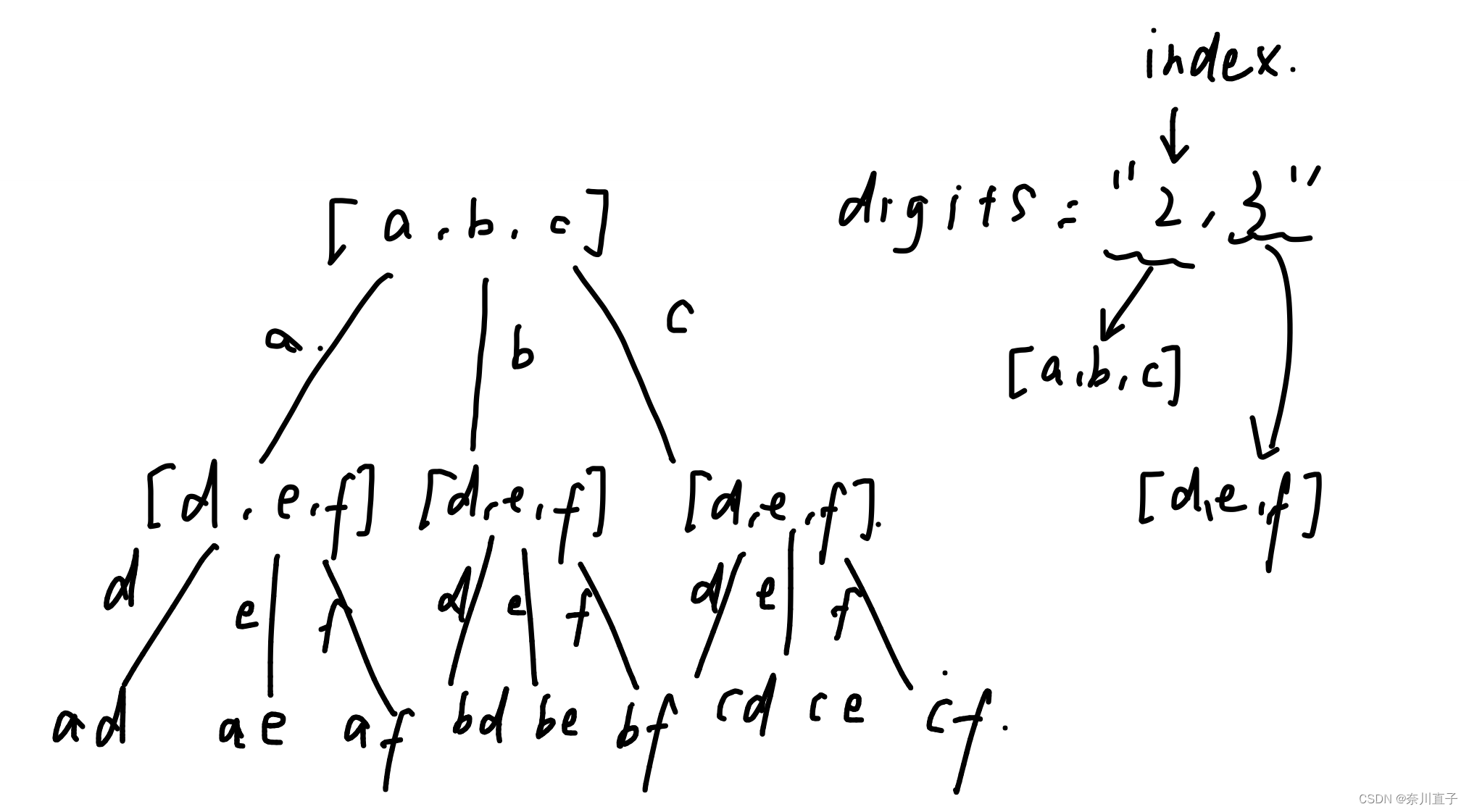
像我这种不爱刷算法的人来说，每题他都给了点提示才解答出来，最终给了我下面这个图，让我实现一下:

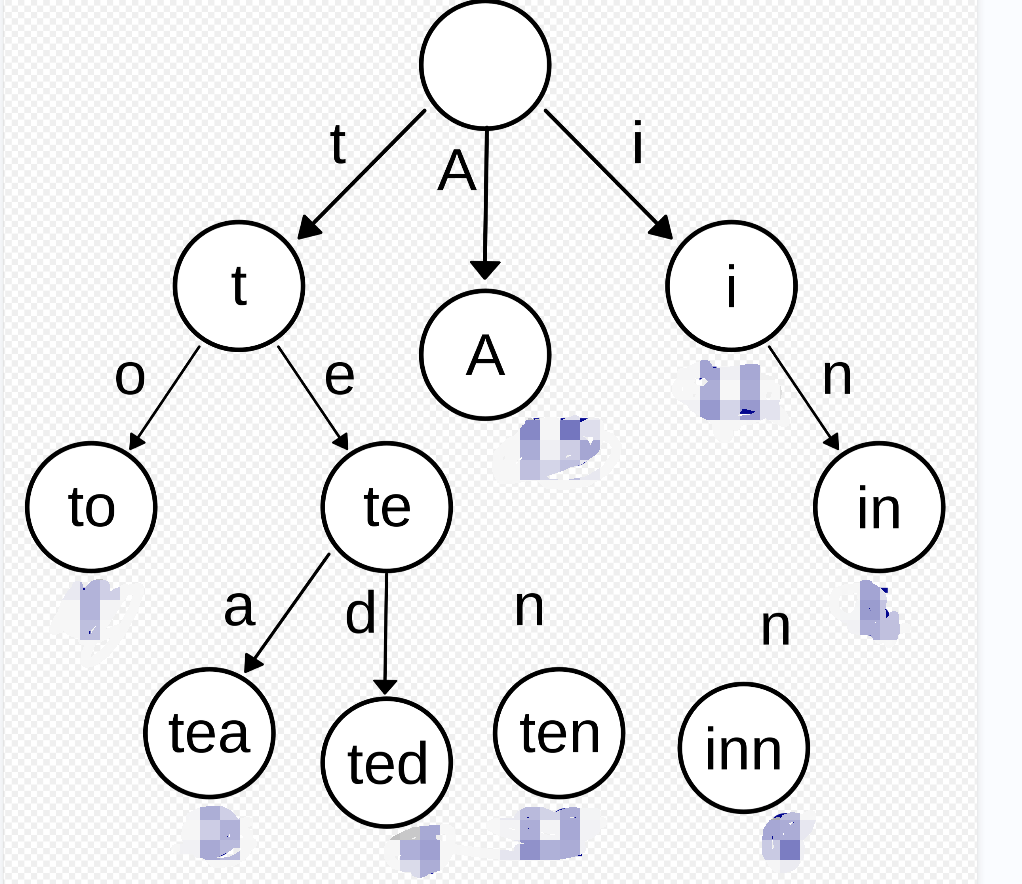
在这里插入图片描述

其实就是经典的前缀树，我这个笨比由于之前没怎么见过，也没写过，写了半天没写出来，最后让我下去写，我大概查了下大致框架，不就是个数组存多条链表的头嘛，其实也就是链表封装了一下。10分钟写了个大概交了，之后的二面只能去线下，那会疫情，我就放弃了，现在想想有点后悔，毕竟是外企955呢;

前缀树介绍

  • 在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。常用与拼写检查自动补全等; 是一种查找结构
  • 他的存储逻辑类似于哈希表，但是它相对于哈希表来说，限制更多，通用性较差，但是它的功能更加强大，可定制性也更强。
    leetcode指路：实现Trie(前缀树)

如图可以查看trie树的基本结构：

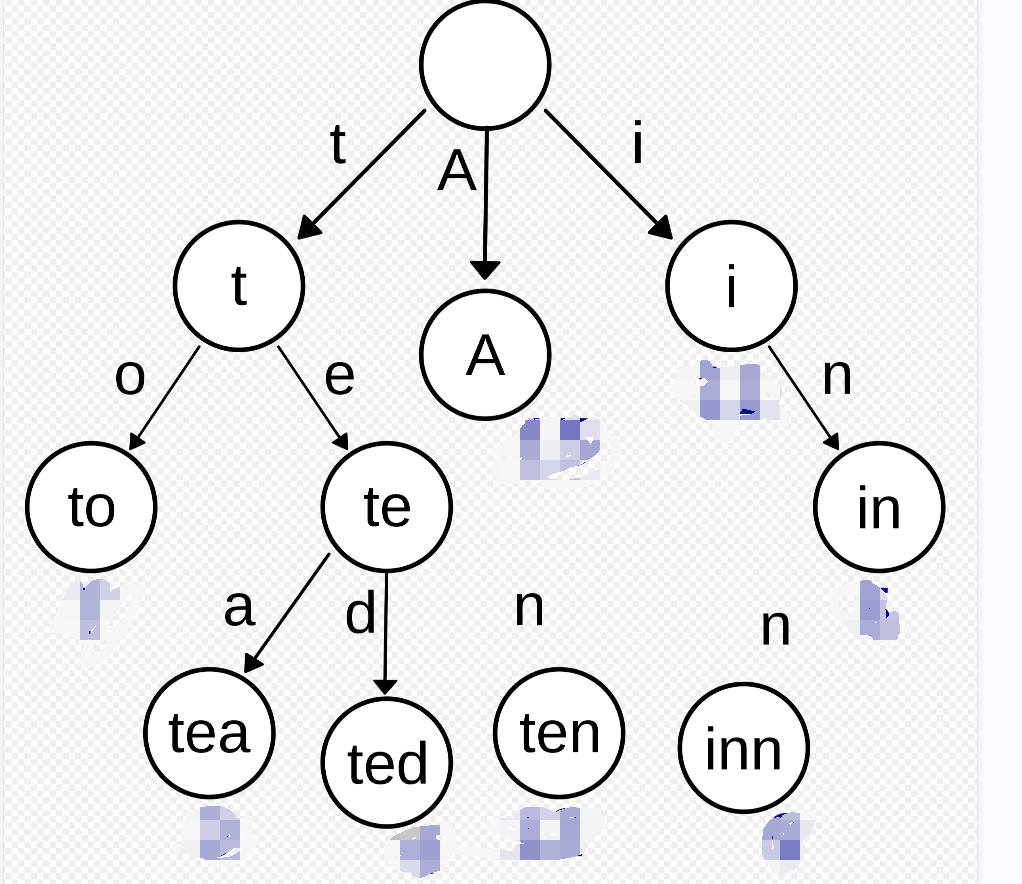
在这里插入图片描述

与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。(这个是前缀树的精髓，也是难理解的地方，他不用存储某个节点的实际字符，他的对应下标映射出了需要存储的字符！)

一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。

一般情况下，不是所有的节点都有对应的值（他们只是前缀），只有叶子节点和部分内部节点所对应的键才有相关的值。

C++实现

核心思想

其实，这个前缀树的实现没有想象中的复杂，觉得难的应该跟我当时一样是第一次看到

仔细想想：

单链表:通过Node中封装的Node* next来找下一个连着的节点;

二叉树:通过Node中封装的Node* left 和 Node* right来找左右孩子节点;

前缀树？

因为维护了26个可能的Node*节点，所以跟上面一个道理，只是不能枚举出来了，用了一个Node*arr[26]来维护，恰巧把这个数组的下标设计成了某个字符的种类，就可以达到利用逻辑下标存储一个实际字符的作用了！

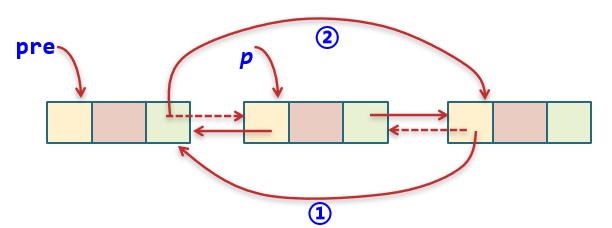
前缀树插入示意图
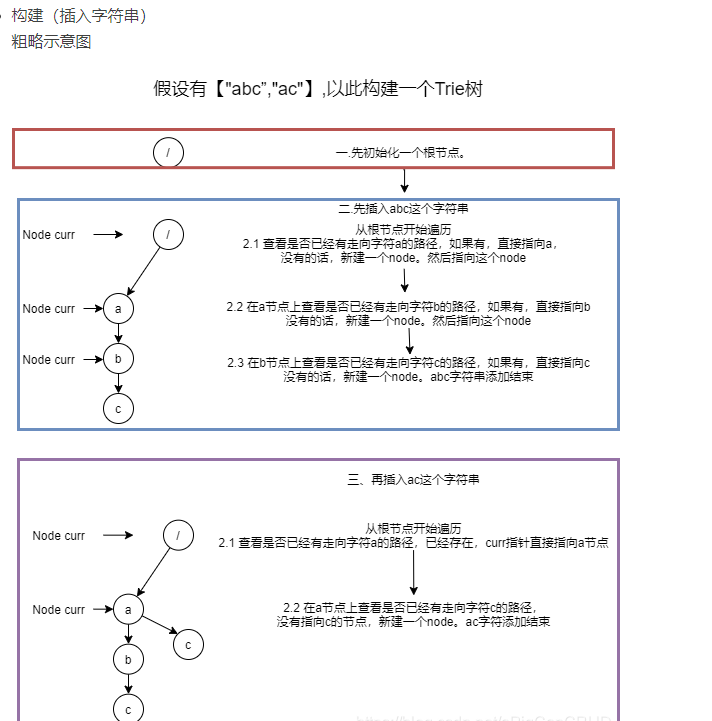
在这里插入图片描述

上图中，每经过一个节点，将该节点的pass值加一，将末尾节点的end值加一。通过这种操作记录所有经过的数据记录

前缀树的插入是灵魂所在，搞懂了之后结构就明白了，不管是查找还是删除无非就是类似对链表的相关操作;

前缀树的大致框架

假设只存小写字符:

#include <iostream>
#include <vector>
#include <string>
using namespace std;

//26 个小写英文字母
#define NUM 26

class Trie{
private:
    Trie* arr[NUM];//多叉树(最大26个分支，因为26个小写字母嘛)
    int end;  //代表word完整单词的个数，0就是无此单词，只是一个前缀;insert一个单词的时候，这个单词的end首次出现就置为1;之后重复插入就end++;
    int pass; //代表以此前缀为公共前缀的节点个数,每次insert的时候会调整;
public:
    Trie() {
        memset(arr,0,sizeof(arr));//每个新节点的映射数组内容置nullptr
	    end = 0;
        ncount = 0; //初始化时以该映射信息字符为前缀的个数为1(这个字符本身算的1)
    }
    //插入单词
    void Insert(string &x)
    {
    }
    //查找 完全匹配字符串x 的数量
    int Find(string &x)
    {
    }
    //查找 前缀为字符串x 的数量
    int FindContain(string& x)
    {

    }
    //删除某个单词(前缀)
    bool Erase(string &x)
    {

    }
    ~Trie()
    {
        //因为new了26个连续的tire*空间，不要某个节点，不要把它对应给下层准备的26个空间也delete掉 防止内存泄漏
        for (int i = 0; i < NUMBER; i++)
		{
			if (nexts[i]){
                delete nexts[i];
            }
            
		}
    }
};
  • 二叉树，父节点之下包含两个节点，分别为左右子节点，分别开辟空间，进行数据存储。
  • 前缀树的结构也是类似的，它的每个节点包含两个部分: 值部分和指针部分。
  • 它的存储方式为：在一棵树上，从根到子节点，分别存储所有目标数据的每一个下标位置上的数据
  • 值部分主要又包含两个数据: 路过该节点的数量为pass， 以该节点为结尾的数量为end。
  • 指针部分主要包含它的所有子节点（比如26个小写字母），记为arr

下面的实现给出了四个接口:

​

  1. Insert插入字符串，给前缀树添加一组数据

其中Insert方法需要注意插入新单词的过程中，路径所有前缀的个数pass+1

  1. Find查找已存入的完整匹配的字符串个数
  2. FindContain 查找已存入的前缀匹配的字符串个数
  3. Erase 从前缀树中擦除一个完整字符串

Erase方法需要注意的是：

  1. 需Find先检查字符串是否存在；
  2. pass == 1 时，代表其下没有任何可能存在的字符子串，所以直接将这个节点delete删除即可；
  3. pass不为1且存在这个字符串，我们把end有效字符串个数-1就行
  4. 移除节点时，需要提前写好析构函数，将其节点开辟的26个Node*内存全部释放，以免出现内存泄漏;

前缀树插入字符串

另外，下面的功能代码不过多解释，代码注释自行理解，核心要点就是用数组下表映射的方式确定前往哪一条链表，之后的寻找和插入等操作都有点像链表的操作，搞个cur指针向后遍历等;

//插入单词
    void Insert(const string &x)
    {
        int size = x.size();
        Node* cur = root;
        cur->pass++;//不管insert啥，我们root空节点的pass相当于必须+1，最终这个root->pass可以代表一共insert了几次=-=
        for (int i = 0; i<size; i++) {
            char index = x[i] - 'a';
            //该字符在当前分支下的映射为空，没有那就new
            if (cur->arr[index] == nullptr) {
                cur->arr[index] = new Node;
            }
          
            cur->arr[index]->pass++; //不管 cur->arr[index] 是new的还是本来就有，insert要路过他了，他的pass+1,

            cur = cur->arr[index];//同时cur下指过去，进行下一个字符的insert
        }

        cur->end++;//insert最终将完整字符串个数end+1
    }

前缀树查找完整的字符串

  //查找 完全匹配字符串 x 的数量 -->end
    int Find(const string &x)
    {
        int size = x.size();
        Node* cur = root;
        for (int i = 0; i < size; i++) {
            char index = x[i] - 'a';
            //搜索到某个字符断了，没有这个完整的字符串x 返回0
            if (cur->arr[index] == nullptr) return 0;

            //没断，继续向下一个字符搜索;
            cur = cur->arr[index];
        }
        return cur -> end;//返回完整字符串x的有效个数end
    }

前缀树查找前缀匹配的字符串

//查找 前缀为字符串 x 的数量 -->pass
    int FindContain(const string& x)
    {
        //与Find一模一样的逻辑，只是最后的return 变了，这体现了Node*封装 int end  和int pass的好处了吧
        int size = x.size();
        Node* cur = root;
        for (int i = 0; i < size; i++) {
            char index = x[i] - 'a';
            if (cur->arr[index] == nullptr) return 0;

            cur = cur->arr[index];
        }
        return cur -> pass;
    }

前缀树删除完整字符串

 //删掉某个完整单词-以及这个单词后面可能存在的所有路径;（end>1 出现了很多次时，只需要end--一下）
    bool Delete(const string &x)
    {
        if (Find(x) == 0) return false;//压根没这个单词，删除失败;

        //有这个单词，我们需要找到他的prev前一个，delete掉他,prev的arr[x]=nullptr!
        Node* cur = root;
        Node* prev = root;
        int size = x.size();
        for (int i = 0; i < size; i++) {
            char index = x[i]-'a';
            //if (cur->arr[index] == nullptr) return false;这句不需要，都过了Find 肯定x每个字符都存在于字典树中
            
            cur->pass--;//别忘了路过的路径都得-1;
            prev = cur;
            cur = cur->arr[index];
        }
        if (cur->end==1) {//代表x所在字符串的个数只有1，直接递归delete删掉它 和 他后面的子串

            delete cur;//这个delete调析构，我们析构已经写好了，防止内存泄漏;
            
            prev->arr[x[size - 1]-'a'] = nullptr; // prev的arr[x最后一个字符-'a'] = nullptr!
        }
        else  cur->end--;//end>1 :end--代表这个节点的有效字符串个数-1，end==1 end-- == 0，这个节点的字符有效个数为0了，但是他因为pass>1,暂时保存 后面的不删;
        //end>1,那就end有效个数-1就行了;
       
        return true;
    }

总结

  • 这个字典树的树结构可以根据需求来进行多样式的处理；比如我为了实现设计的功能，每个节点都保存了pass和end俩int方便功能记录和函数内的使用;
  • 字典树本质上是牺牲空间，换查找同前缀的字符串提升时间效率的一种措施，但是我们这种每个节点都开26个数组的方式是非常浪费空间的，比如只有一个有效字符下标，其他25个nullptr都浪费了，而且在大量相同的前缀下就是单链表，浪费更严重。
  • 这时候我们可以把Node*arr[26]数组换成map<char,Node*>这样搞(每层某一个char只会出现一次，所以char做key没问题)，需要配对啥就insert给红黑树中添加啥,大大节省空间;

所以说这个树没有啥固定玩法，可塑性太强了…这可能也是不刷题的我不常见的愿因？

完整代码

#include <iostream>
#include <vector>
#include <string>
using namespace std;

//26 个小写英文字母
#define NUM 26

//前缀树节点
class Node {
public:
    Node* arr[NUM];//多叉树(最大26个分支，因为26个小写字母嘛)
    int end;  //代表
    int pass; //代表以此前缀为公共前缀的节点个数,每次insert的时候会调整
    Node()
    {
        end = 0;
        pass = 0;
        memset(arr, 0, sizeof(arr));
    }

    ~Node()
    {
     
        //这里有点递归的意思，除了删除当前节点，更重要的是如果当前节点的子节点还有非空。递归delete掉！
        for (int i = 0; i < NUM; i++)
        {
            if (arr[i]!=nullptr) delete arr[i];
        }
    }
};
//前缀树主体
class Trie{
public:
    Node* root = nullptr;
public:
    Trie() {
        root = new Node;
    }
    //插入单词
    void Insert(const string &x)
    {
        int size = x.size();
        Node* cur = root;
        cur->pass++;//不管insert啥，我们root空节点的pass相当于必须+1，最终这个root->pass可以代表一共insert了几次=-=
        for (int i = 0; i<size; i++) {
            char index = x[i] - 'a';
            //该字符在当前分支下的映射为空，没有那就new
            if (cur->arr[index] == nullptr) {
                cur->arr[index] = new Node;
            }
          
            cur->arr[index]->pass++; //不管 cur->arr[index] 是new的还是本来就有，insert要路过他了，他的pass+1,

            cur = cur->arr[index];//同时cur下指过去，进行下一个字符的insert
        }

        cur->end++;//insert最终将完整字符串个数end+1
    }

    //查找 完全匹配字符串 x 的数量 -->end
    int Find(const string &x)
    {
        int size = x.size();
        Node* cur = root;
        for (int i = 0; i < size; i++) {
            char index = x[i] - 'a';
            //搜索到某个字符断了，没有这个完整的字符串x 返回0
            if (cur->arr[index] == nullptr) return 0;

            //没断，继续向下一个字符搜索;
            cur = cur->arr[index];
        }
        return cur -> end;//返回完整字符串x的有效个数end
    }
    //查找 前缀为字符串 x 的数量 -->pass
    int FindContain(const string& x)
    {
        //与Find一模一样的逻辑，只是最后的return 变了，这体现了Node*封装 int end  和int pass的好处了吧
        int size = x.size();
        Node* cur = root;
        for (int i = 0; i < size; i++) {
            char index = x[i] - 'a';
            if (cur->arr[index] == nullptr) return 0;

            cur = cur->arr[index];
        }
        return cur -> pass;
    }
    //删掉某个完整单词-以及这个单词后面可能存在的所有路径;（end>1 出现了很多次时，只需要end--一下）
    bool Delete(const string &x)
    {
        if (Find(x) == 0) return false;//压根没这个单词，删除失败;

        //有这个单词，我们需要找到他的prev前一个，delete掉他,prev的arr[x]=nullptr!
        Node* cur = root;
        Node* prev = root;
        int size = x.size();
        for (int i = 0; i < size; i++) {
            char index = x[i]-'a';
            //if (cur->arr[index] == nullptr) return false;这句不需要，都过了Find 肯定x每个字符都存在于字典树中
            
            cur->pass--;//别忘了路过的路径都得-1;
            prev = cur;
            cur = cur->arr[index];
        }
        if (cur->end==1) {//代表x所在字符串的个数只有1，直接递归delete删掉它 和 他后面的子串

            delete cur;//这个delete调析构，我们析构已经写好了，防止内存泄漏;
            
            prev->arr[x[size - 1]-'a'] = nullptr; // prev的arr[x最后一个字符-'a'] = nullptr!
        }
        else  cur->end--;//end>1 :end--代表这个节点的有效字符串个数-1，end==1 end-- == 0，这个节点的字符有效个数为0了，但是他因为pass>1,暂时保存 后面的不删;
        //end>1,那就end有效个数-1就行了;
       
        return true;
    }

};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/179316.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【MySQL进阶】MySQL视图详解

【MySQL进阶】MySQL视图详解

序号系列文章6【MySQL基础】MySQL单表操作详解7【MySQL基础】运算符及相关函数详解8【MySQL基础】MySQL多表操作详解9【MySQL进阶】MySQL事务详解文章目录前言1&#xff0c;视图1.1&#xff0c;视图概述1.2&#xff0c;视图使用环境1.3&#xff0c;视图创建格式1.4&#xff0c;…
阅读更多...
【C语言课堂】 函数递归

【C语言课堂】 函数递归

欢迎来到 Claffic 的博客 &#x1f49e;&#x1f49e;&#x1f49e; 前言&#xff1a; 时隔多日&#xff0c;来还欠大家的 C 语言学习啦&#xff0c;上期讲了函数&#xff0c;其实函数中应该包括函数递归的&#xff0c;这里单独拿出来讲解的原因是函数递归属于重难知识&#xf…
阅读更多...
【编程入门】开源记事本（Flutter版）

【编程入门】开源记事本（Flutter版）

背景 前面已输出多个系列&#xff1a; 《十余种编程语言做个计算器》 《十余种编程语言写2048小游戏》 《17种编程语言10种排序算法》 《十余种编程语言写博客系统》 《十余种编程语言写云笔记》 本系列对比云笔记&#xff0c;将更为简化&#xff0c;去掉了网络调用&#xff0…
阅读更多...
数据结构入门(力扣算法)

数据结构入门(力扣算法)

数据结构入门前面的题号为力扣的题号数组的217. 存在重复元素53. 最大子数组和1. 两数之和88. 合并两个有序数组350. 两个数组的交集 II121. 买卖股票的最佳时机566. 重塑矩阵118. 杨辉三角36. 有效的数独73. 矩阵置零字符串的387. 字符串中的第一个唯一字符383. 赎金信242. 有…
阅读更多...
LeetCode 437. 路径总和 III

LeetCode 437. 路径总和 III

LeetCode 437. 路径总和 III 给定一个二叉树的根节点 root &#xff0c;和一个整数 targetSum &#xff0c;求该二叉树里节点值之和等于 targetSum 的 路径 的数目。 路径 不需要从根节点开始&#xff0c;也不需要在叶子节点结束&#xff0c;但是路径方向必须是向下的&#xff…
阅读更多...
JUC面试（十一）——LockSupport

JUC面试（十一）——LockSupport

可重入锁 可重入锁又名递归锁 是指在同一个线程在外层方法获取锁的时候&#xff0c;再进入该线程的内层方法会自动获取锁(前提&#xff0c;锁对象得是同一个对象)&#xff0c;不会因为之前已经获取过的锁还没释放而阻塞。 Java中ReentrantLock和synchronized都是可重入锁&am…
阅读更多...
第一章 概述

第一章 概述

第一章 概述 1.1 计算机网络在信息时代中的作用 21世纪的一些重要特征 数字化&#xff0c;网络化和信息化 以网络为核心的信息时代 互联网的两个重要基本特点 连通性共享&#xff08;资源共享&#xff09; 1.2 互联网概述 计算机网络由若干个结点货连接这些结点的链路组成…
阅读更多...
【唐诗学习】四、边塞诗派代表

【唐诗学习】四、边塞诗派代表

四、边塞诗派代表 边塞诗派起源 盛唐是中国历史上一个空前的盛世&#xff0c;国库丰盈&#xff0c;社会十分安定&#xff0c;百姓的幸福指数高。 盛唐是中国历史上一个空前的盛世&#xff0c;国库丰盈&#xff0c;社会十分安定&#xff0c;百姓的幸福指数高。唐太宗以后的几个…
阅读更多...
Citadel——Dusk网络的Zero-Knowledge KYC解决方案

Citadel——Dusk网络的Zero-Knowledge KYC解决方案

1. 引言 近期&#xff0c;Dusk网络宣布其已支持名为Citadel的Zero-Knowledge KYC解决方案&#xff0c;使得用户和机构可控制其权限以及个人信息分享。该架构可用于all claim-based KYC requests&#xff0c;并让用户完全控制他们共享的信息以及与谁共享信息&#xff0c;同时完…
阅读更多...
详解Java中的BIO、NIO、AIO

详解Java中的BIO、NIO、AIO

1、 详解Java中的BIO、NIO、AIO 1.1、引言 IO流是Java中比较难理解的一个知识点&#xff0c;但是IO流在实际的开发场景中经常会使用到&#xff0c;比如Dubbo底层就是NIO进行通讯。本文将介绍Java发展过程中出现的三种IO&#xff1a;BIO、NIO以及AIO&#xff0c;重点介绍NIO。…
阅读更多...
【c语言进阶】常见的静态通讯录

【c语言进阶】常见的静态通讯录

&#x1f680;write in front&#x1f680; &#x1f4dc;所属专栏&#xff1a;c语言学习 &#x1f6f0;️博客主页&#xff1a;睿睿的博客主页 &#x1f6f0;️代码仓库&#xff1a;&#x1f389;VS2022_C语言仓库 &#x1f3a1;您的点赞、关注、收藏、评论&#xff0c;是对我…
阅读更多...
2.H3CNE-网络参考模型

2.H3CNE-网络参考模型

OSI参考模型产生背景各大IT设备厂商只支持自己的私有协议&#xff0c;跨厂商设备兼容性差用户购买和维护成本高不利于网络技术发展概念定义了网络中设备所遵守的层次结构优点开放的标准化接口&#xff0c;协议不再封闭多厂商设备兼容易于理解、学习和更新协议标准实现模块化工程…
阅读更多...
【Leetcode刷题】141、环形链表

【Leetcode刷题】141、环形链表

原题链接&#xff1a;https://leetcode.cn/problems/linked-list-cycle/?favorite2cktkvj给你一个链表的头节点 head &#xff0c;判断链表中是否有环。如果链表中有某个节点&#xff0c;可以通过连续跟踪 next 指针再次到达&#xff0c;则链表中存在环。 为了表示给定链表中的…
阅读更多...
Python数据可视化（二）使用统计函数绘制简单图形

Python数据可视化（二）使用统计函数绘制简单图形

该文会讲解一些大家比较熟悉却又经常混淆的统计图形&#xff0c;掌握这些统计图形可以对数据可视化有一个深入理解&#xff0c;并正确使用。2.1 函数 bar()——用于绘制柱状图函数功能&#xff1a;在 x 轴上绘制定性数据的分布特征。调用签名&#xff1a;plt.bar(x,y)。参数说明…
阅读更多...
day21|216.组合总和III、17.电话号码的字母组合

day21|216.组合总和III、17.电话号码的字母组合

216.组合总和III 找出所有相加之和为 n 的 k 个数的组合&#xff0c;且满足下列条件&#xff1a; 只使用数字1到9每个数字 最多使用一次 返回所有可能的有效组合的列表 。该列表不能包含相同的组合两次&#xff0c;组合可以以任何顺序返回。 示例 1: 输入: k 3, n 7 输出: …
阅读更多...
说说配置中心

说说配置中心

什么是配置中心在微服务的环境下,将项目需要的配置信息保存在配置中心,需要读取时直接从配置中心读取,方便配置管理的微服务工具可以将部分yml文件的内容保存在配置中心一个微服务项目有很多子模块,这些子模块可能在不同的服务器上,如果有一些统一的修改,需要逐一修改这些子模块…
阅读更多...
python数据可视化开发：Matplotlib库基础知识

python数据可视化开发：Matplotlib库基础知识

文章目录前言01.工具栏组件02.图表数据03.设置字体字典&#xff08;1&#xff09;全局字体样式&#xff08;2&#xff09;常用中文字体对应名称&#xff08;3&#xff09;查询当前系统所有字体04.图像配置实例05.图表标题06.文本组件07.坐标轴标签组件08.网格组件09.绘制折线10…
阅读更多...
【头歌】双向链表的基本操作

【头歌】双向链表的基本操作

双向链表的基本操作第1关&#xff1a;双向链表的插入操作任务描述本关任务&#xff1a;编写双向链表的插入操作函数。相关知识双链表中用两个指针表示结点间的逻辑关系&#xff1a;指向其前驱结点的指针域prior&#xff0c;指向其后继结点的指针域next。双向链表的结点结构如图…
阅读更多...
MySQL数据库面试题[万字汇总]

MySQL数据库面试题[万字汇总]

1) MySQL数据库相关错题本1、存储引擎相关1、MySql的存储引擎的不同MySQL存储引擎主要有InnoDB, MyISAM, Memory, 这三个区别在于:Memory是内存数据引擎, 会断电重启(在双M或者主从架构下会产生较多异常), 且不支持行级锁. 默认索引是数组索引, 支持B索引InnoDB和MyISAM的区别:…
阅读更多...
流批一体计算引擎-5-[Flink]的Python Table API和SQL程序

流批一体计算引擎-5-[Flink]的Python Table API和SQL程序

参考Flink从入门到入土&#xff08;详细教程&#xff09; 参考flink的默认窗口触发机制 参考彻底搞清Flink中的Window 参考官方Python API文档 1 IDEA中运行Flink 从Flink 1.11版本开始, PyFlink 作业支持在 Windows 系统上运行&#xff0c;因此您也可以在 Windows 上开发和…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023