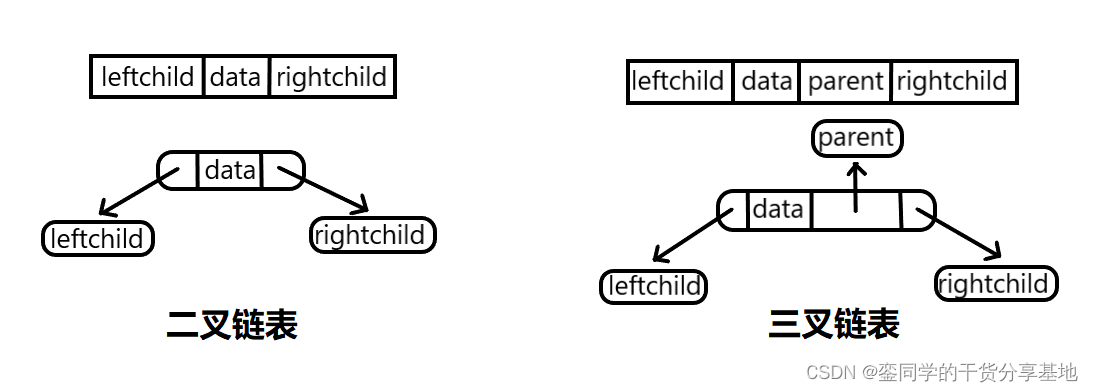
数据结构入门
- 前面的题号为力扣的题号
- 数组的
- 217. 存在重复元素
- 53. 最大子数组和
- 1. 两数之和
- 88. 合并两个有序数组
- 350. 两个数组的交集 II
- 121. 买卖股票的最佳时机
- 566. 重塑矩阵
- 118. 杨辉三角
- 36. 有效的数独
- 73. 矩阵置零
- 字符串的
- 387. 字符串中的第一个唯一字符
- 383. 赎金信
- 242. 有效的字母异位词
- 链表
- 141. 环形链表
- 21. 合并两个有序链表
- 203. 移除链表元素
- 206. 反转链表
- 83. 删除排序链表中的重复元素
- 栈和队列
- 20. 有效的括号
- 232. 用栈实现队列
- 树
- 144. 二叉树的前序遍历
- 94. 二叉树的中序遍历
- 145. 二叉树的后序遍历
- 102. 二叉树的层序遍历
- 104. 二叉树的最大深度
- 101. 对称二叉树
- 226. 翻转二叉树
- 112. 路径总和
- 700. 二叉搜索树中的搜索
- 701. 二叉搜索树中的插入操作
- 98. 验证二叉搜索树
- 653. 两数之和 IV - 输入二叉搜索树
- 235. 二叉搜索树的最近公共祖先
前面的题号为力扣的题号
数组的
217. 存在重复元素
问题

思路
- 排序,选用快速排序
- 两两相邻比较是否存在相同。
代码
class Solution {
public boolean containsDuplicate(int[] nums) {
// 先将数组排序
kp(nums, 0, nums.length-1);
// 局部两两比较不能相等
for(int i=1; i<nums.length; i++) {
if(nums[i-1]==nums[i]){
return true;
}
}
return false;
}
// 有时间复杂度要求,这里调用快排
static void kp(int nums[], int low, int high){
if(low<high) {
int p = kp_p(nums, low, high);
// 左表快排
kp(nums, low, p-1);
// 右表快排
kp(nums, p+1, high);
}
}
static int kp_p(int nums[], int low, int high){
int t = nums[low];
while (low<high) {
while(low<high && nums[high]>=t) high--;
nums[low] = nums[high];
while(low<high && nums[low]<=t) low++;
nums[high] = nums[low];
}
nums[low] = t;
return low;
}
}
53. 最大子数组和
问题
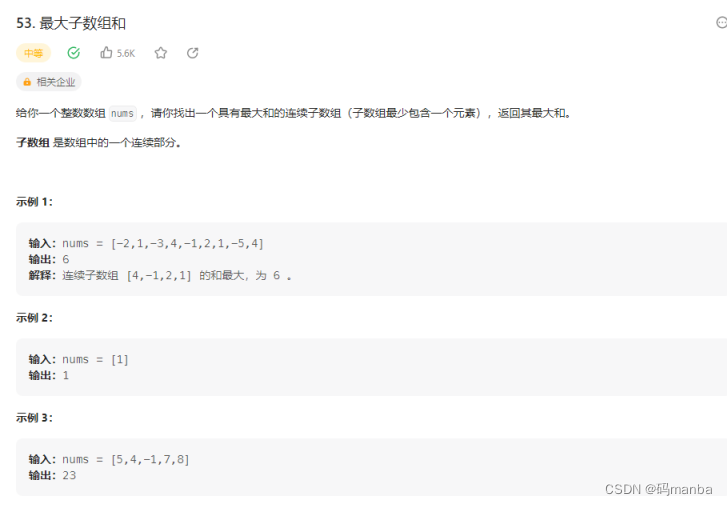
思想
- 注意本题可以用动态规划的思路去解决
- 要求的为最大连续的和最大, 我们要找到那个有关联的子问题
- 子问题分析
3.1 到第一个数位置结束, 最大连续数就是第一个位置的数
3.2 到第二个位置的数结束, 最大连续和,若前一个位置最大连续为大于0,则最大连续要加上前面的, 如果前一个数的最大连续为负数, 则自己本身就是最大连续和
3.3 所以每个最大连续和就和到前面位置的最大连续和有直接联系。 这就划分成求到每个位置最大连续和的子问题的处理
代码
class Solution {
public int maxSubArray(int[] nums) {
// 创建一个以i处元素为结尾的连续最大和数组 dp
int []dp = new int[nums.length];
dp[0] = nums[0];
// dp[i] : 注意dp[1] 即 dp[0] 如果是大于0, 则 到dp[1] 最大连续为 dp[0] + nums[1]
// 如果dp[0] 小于0 , 则dp[1] 最大连续就是 nums[1] 本身
for(int i=1; i<nums.length; i++) {
if(dp[i-1]>0) {
dp[i] = dp[i-1] + nums[i];
}else {
dp[i] = nums[i];
}
}
// 此时dp数组中保存了以i位置为结束的最大的连续和, 我们只需找到以某个位置结束的最大值即可
int max = dp[0];
for(int i=1; i<dp.length; i++) {
if(dp[i] > max) {
max = dp[i];
}
}
return max;
}
}
1. 两数之和
问题

思想
- 只要求任意两元素加和为目标值, 并且要这两个数不为同一个位置的元素
- 题目要求 时间复杂度为 n方, 所以两层循环解决就可以
代码
class Solution {
public int[] twoSum(int[] nums, int target) {
int indexs[] = new int[2]; // 用来保存和为目标值的两个下标
for(int i=0; i<nums.length; i++) {
for(int j=0; j<nums.length; j++) {
if(nums[i] + nums[j] == target && i!=j) {
indexs[0]=i;
indexs[1]=j;
return indexs;
}
}
}
return indexs;
}
}
88. 合并两个有序数组
题目
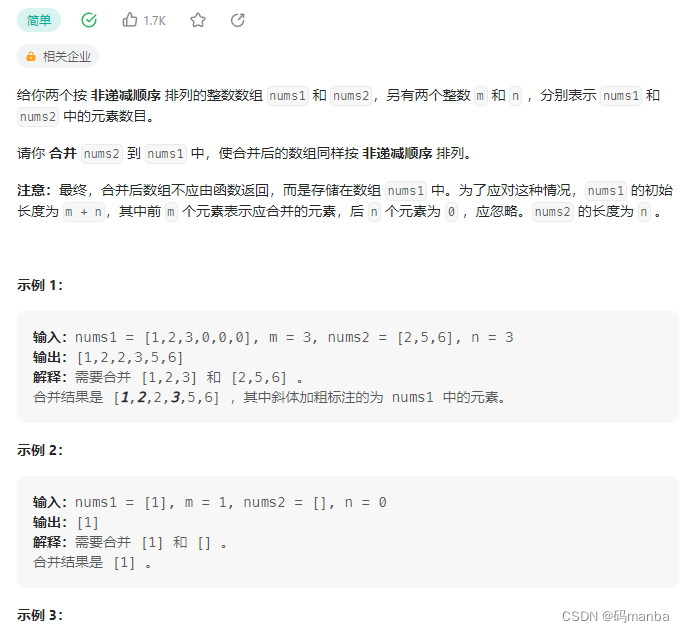
思想
- 本质上就是完成一个归并操作
- 特别注意归并结束后,一定检查两个数组的元素是否还有元素未被归并进去
代码
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 先创建一个临时的数组
int numst[] = new int[n+m];
int i,j,k;
// 先用归并,归并到一个临时数组
for(i=0,j=0,k=0; i<m&&j<n;) {
if(nums1[i]<=nums2[j]) {
numst[k++] = nums1[i++];
}else {
numst[k++] = nums2[j++];
}
}
// 可能有一部分归并结束,另一个数组还有元素未归并
while(i<m) {
numst[k++] = nums1[i++];
}
while(j<n) {
numst[k++] = nums2[j++];
}
// 再将临时数组复制到nums1
for(i=0; i<m+n; i++) {
nums1[i] = numst[i];
}
}
}
350. 两个数组的交集 II
问题
思想
- 首先将两个数组进行排序
- 两个有序的数组,相同就输出。不同的话,就小的下标递增
- 当有一个下标走到尽头,就结束了。
代码
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
// 采用排序 + 双指针的方式
// 先将nums1与nums2进行排序
kp(nums1, 0, nums1.length-1);
kp(nums2, 0, nums2.length-1);
// 定义两个指针,分别指向两个数组的起始位置
int p1=0,p2=0,k=0;
int numst[] = new int[nums1.length + nums2.length];
while(p1<nums1.length && p2<nums2.length) {
if(nums1[p1] == nums2[p2]) {
//相等的时候保存
numst[k++] = nums1[p1];
p1++;
p2++;
}else if(nums1[p1] > nums2[p2]) {
// 小的数后移
p2++;
}else {
p1++;
}
}
return Arrays.copyOfRange(numst, 0, k);
}
// 快排
void kp(int d[], int low, int high){
if(low<high) {
// 一次划分,确定元素的位置
int p = kp_hf(d, low, high);
// 将上面的划分左右侧的子表 分别再递归划分
kp(d, low, p-1);
kp(d, p+1, high);
}
}
// 一次快排划分
int kp_hf(int d[], int low, int high) {
int p = d[low];
while(low<high) {
while(low<high && d[high] >= p) high--;
d[low] = d[high];
while(low<high && d[low] <= p) low++;
d[high] = d[low];
}
d[low] = p;
return low;
}
}
121. 买卖股票的最佳时机
问题
思想
- 用动归的思想,在代码有详细注释
- dp[i] 动态记录截至第i天的最低价格(用于购入)
- max 用于动态记录 当天股价卖出, 与最低点购入的利润是否为最大
代码
class Solution {
public int maxProfit(int[] prices) {
// 根据动态规划的思想去解决
// 1. 截至第i是否为最低点, 与截至其前一天是不是最低点有关联,第i天最低,则截至第i天,保留第i天,第i天不是最低点,则保留截至第i-1天最低点数
// 2. 今天的股价卖出(今天的股价减去 截至今天的最低价的最高值)
int max=0;
int dp[] = new int[prices.length];
dp[0] = prices[0]; // dp保存截至第i天买入的价格的最低价
for(int i=1; i<prices.length; i++) {
// 不断判断截至第i天的最低购入价格
// 今天是最低价,则截至今天最低价是今天的价, 否则为前i-1天的最低价
dp[i] = dp[i-1] < prices[i] ? dp[i-1] : prices[i];
// 判断今天的价格减去截至今天的最低价dp[i]是否为最大利润
max = max>(prices[i] - dp[i]) ? max : (prices[i] - dp[i]);
}
return max;
}
}
566. 重塑矩阵
问题

思想
- 注意重塑的时候,原矩阵和重塑后的矩阵是否是元素数相同的矩阵.
- 重塑的时候遍历原矩阵, 新的矩阵的列标到指定数的时候做行标和列标的调整即可。
代码
class Solution {
public int[][] matrixReshape(int[][] mat, int r, int c) {
int [][] jz = new int[r][c]; // 重塑后矩阵的维度
int m=0,n=0; // 用于记录新矩阵每行一共多少元素
// 新矩阵的元素数应该与原矩阵元素数一致
if(mat.length * mat[0].length != r * c) {
// 不一致时返回原矩阵
return mat;
}
// 遍历原矩阵
for(int i=0; i<mat.length; i++) {
for(int j=0; j<mat[0].length; j++) {
if(n==c) {
// 新矩阵要换行了
m++; // 行号自增
n=0; // 列号变0
}
jz[m][n++] = mat[i][j];
}
}
return jz;
}
}
118. 杨辉三角
问题
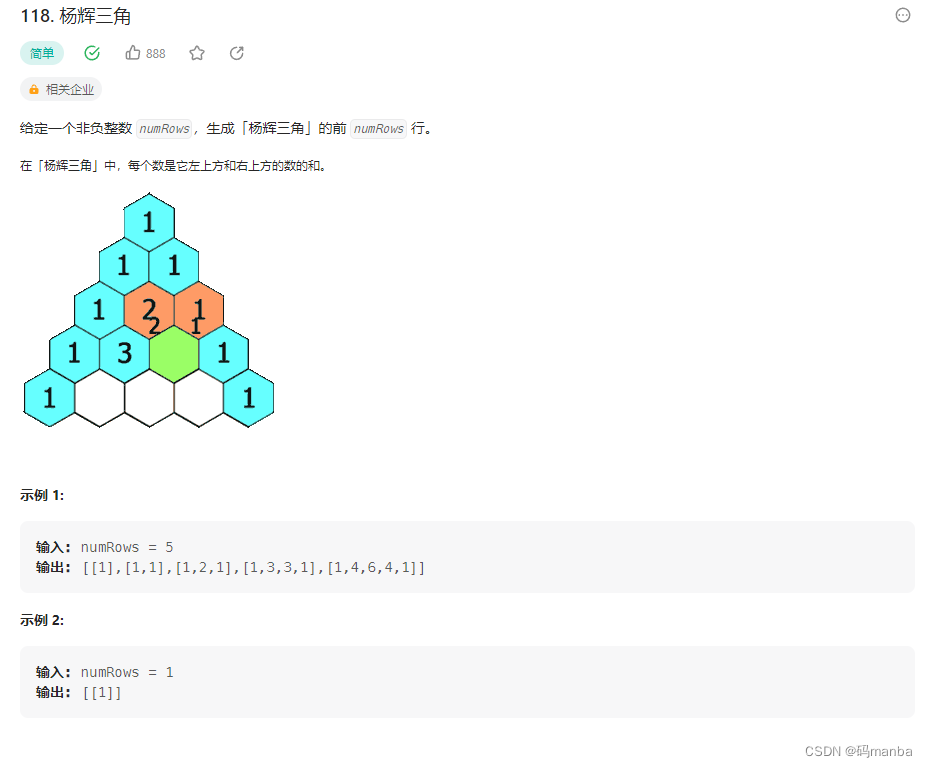
思想
- 注意用list实现的时候
代码
class Solution {
public List<List<Integer>> generate(int numRows) {
// 创建一个二维的列表结构
List<List<Integer>> list = new ArrayList<>();
for(int i=0; i<numRows; i++) {
// 创建每行的列表
ArrayList<Integer> row = new ArrayList<>();
for(int j=0; j<=i; j++) {
if(j==0 || j==i) { // 两斜边位置为1
row.add(1);
} else {
row.add(list.get(i-1).get(j-1) + list.get(i-1).get(j));
}
}
list.add(row); // 将本行添加进去
}
return list;
}
}
36. 有效的数独
问题

思想
- 用两个二维数组分别记录, 某数字在所在行、所在列出现的次数
- 用三维数组表示 该数字 所在小区域内出现的 次数。
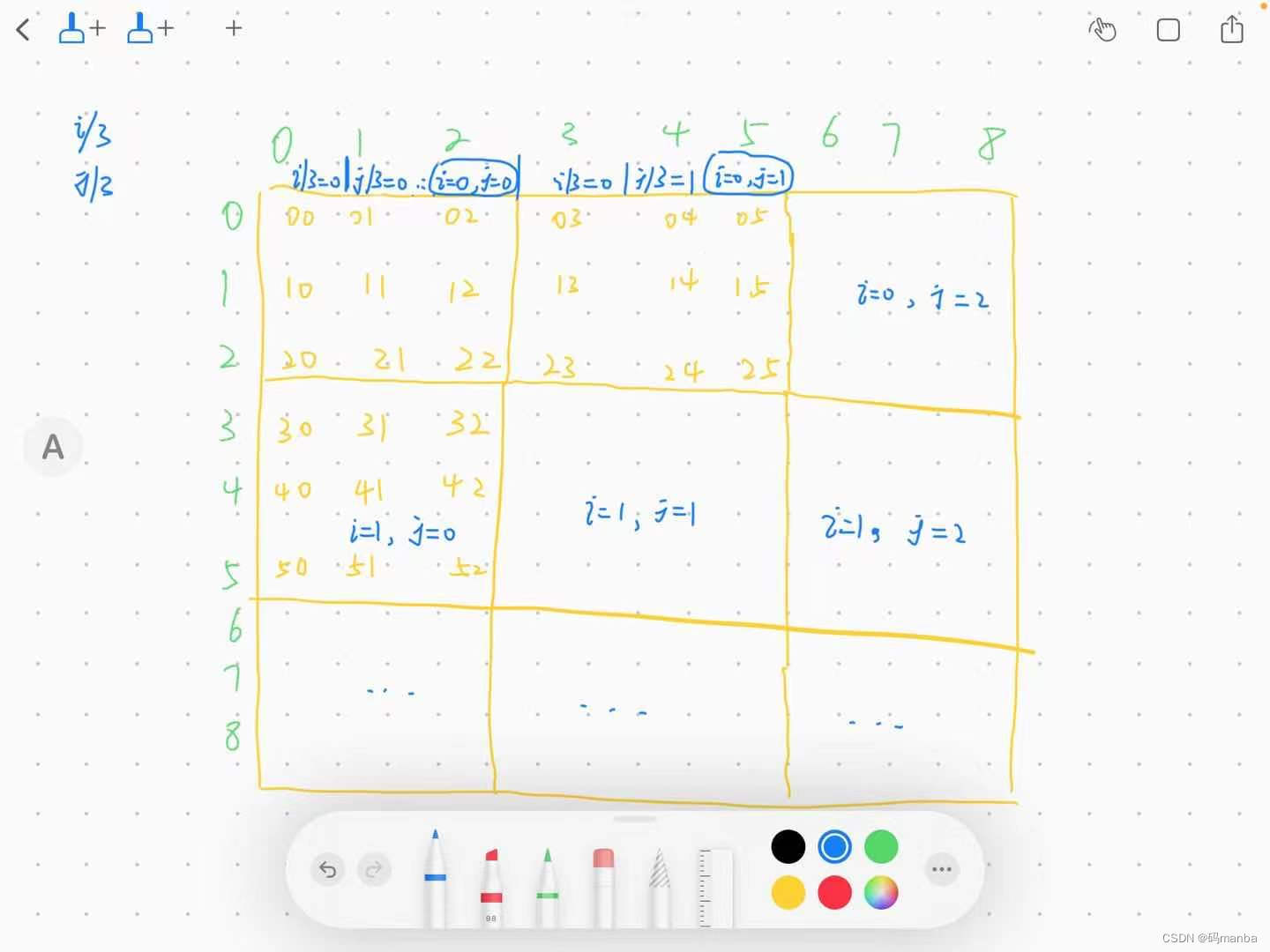
代码
class Solution {
public boolean isValidSudoku(char[][] board) {
// 创建一个二维数组, 记录当前行的数据各有多少个
// 行标表示第几行, 列标表示的是具体的数值 row[i][j]表示第i行值为j的的数的个数
int row[][] = new int[9][9];
// 创建一个用于记录每列的元素个数统计的二维数组
int col[][] = new int[9][9];
// 创建一个三维数组,统计 9个3*3的小矩形内的元素个数 i/3 , j/3 正好划分为九个
int juzhen[][][] = new int [3][3][9];
// 遍历这个9*9的二维数组, 并记录board[i][j] 这个元素值,在所在行、所在列、所在小矩形区域内的个数
for(int i=0; i<9; i++) {
for(int j=0; j<9; j++) {
if(board[i][j] != '.') {
//有元素时,不为.
int index = board[i][j] - '1';
// 记录该元素 在所在行的出现次数
row[i][index]++;
// 记录该元素 在所在列出现的次数
col[j][index]++;
// 记录该元素在所在矩阵内出现的次数
juzhen[i/3][j/3][index]++;
// 判断在所在行、列、矩阵是否超过1次,超过就不是有效数独
if(row[i][index]>1 || col[j][index]>1 || juzhen[i/3][j/3][index]>1) {
return false;
}
}
}
}
// 有效返回true
return true;
}
}
73. 矩阵置零
问题
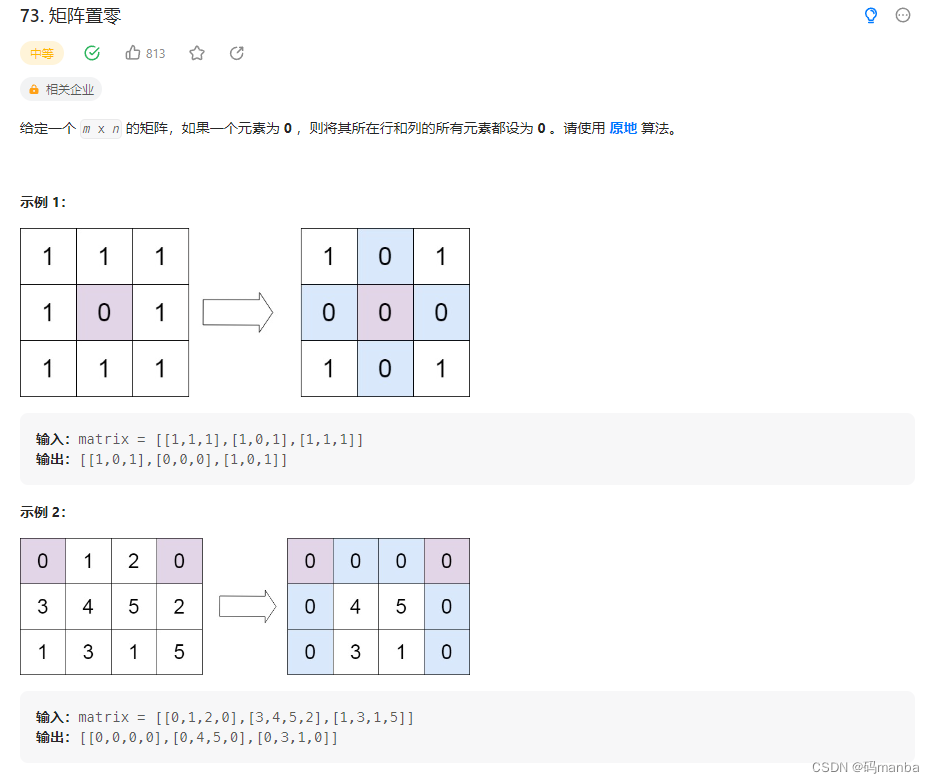
思想
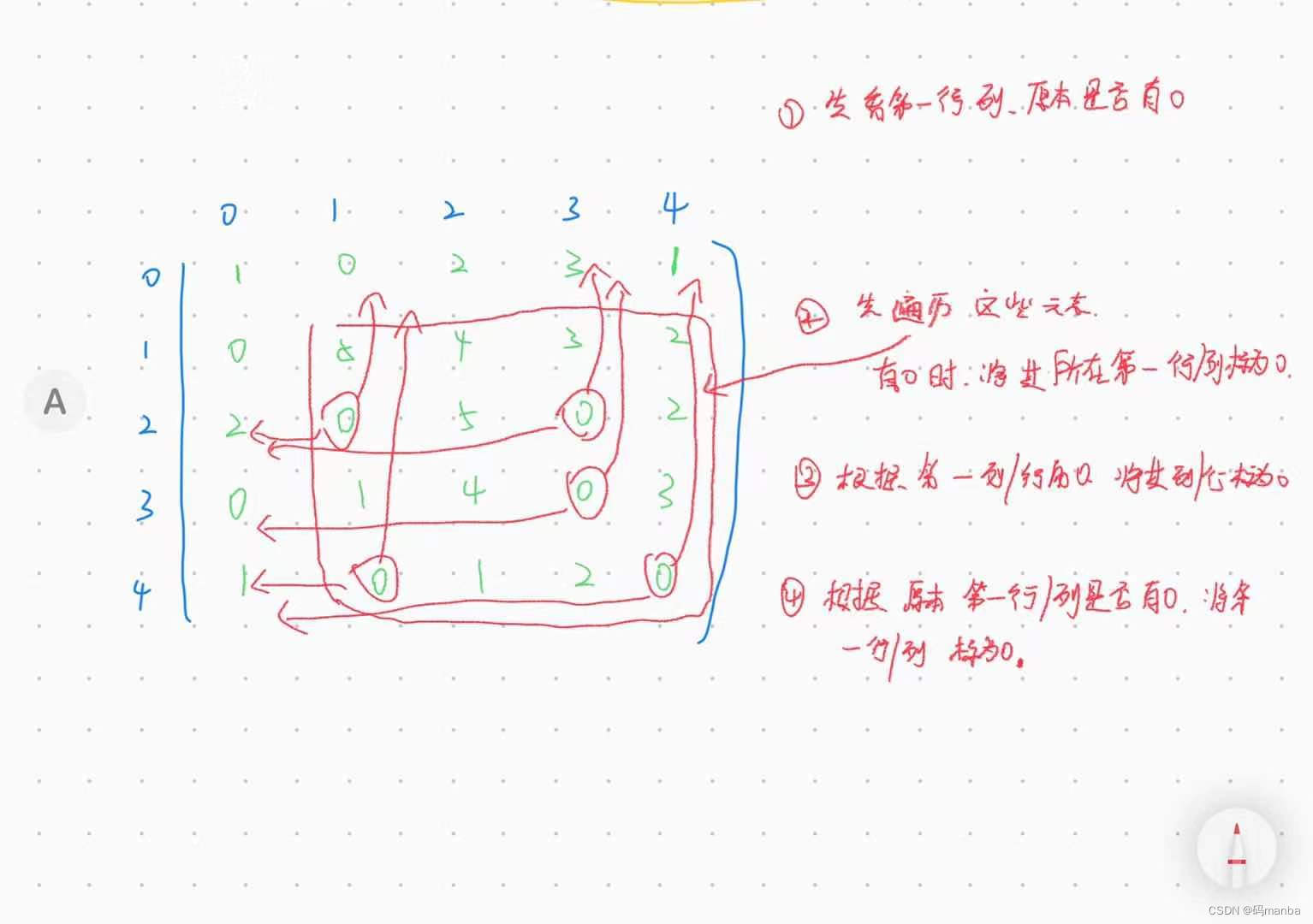
代码
class Solution {
public void setZeroes(int[][] matrix) {
boolean col0falg = false, row0falg=false; // 标记第一行/列 原数组是否有零
int rowLen = matrix.length, colLen = matrix[0].length;
for(int i=0; i<rowLen; i++) {
// 判断第一列原本是否有0
if(matrix[i][0] == 0) {
col0falg = true;
}
}
for(int j=0; j<colLen; j++) {
// 判断第一行原本是否有0
if(matrix[0][j] == 0) {
row0falg = true;
}
}
// 判断除了第一行、列的元素是否为0, 为0时标记所在行列的第一行列为0
for(int i=1; i<rowLen; i++) {
for(int j=1; j<colLen; j++) {
if(matrix[i][j] == 0) { // 当前元素为0则↓
// 设置第一行/列的所在位置为0
matrix[i][0] = matrix[0][j] = 0;
}
}
}
// 将第一行/列 为0的所在行列设为0
for(int i=1; i<rowLen; i++) {
for(int j=1; j<colLen; j++) {
if(matrix[i][0] == 0 || matrix[0][j] == 0) { // 根据当前行列有0设置该元素为0
matrix[i][j] = 0;
}
}
}
// 根据原本第一行列是否有0, 设置第一行列为0
if(col0falg) {
// 第一列有0
for(int i=0; i<rowLen; i++) {
matrix[i][0] = 0;
}
}
if(row0falg) {
// 第一行有0
for(int i=0; i<colLen; i++) {
matrix[0][i] = 0;
}
}
}
}
字符串的
387. 字符串中的第一个唯一字符
问题
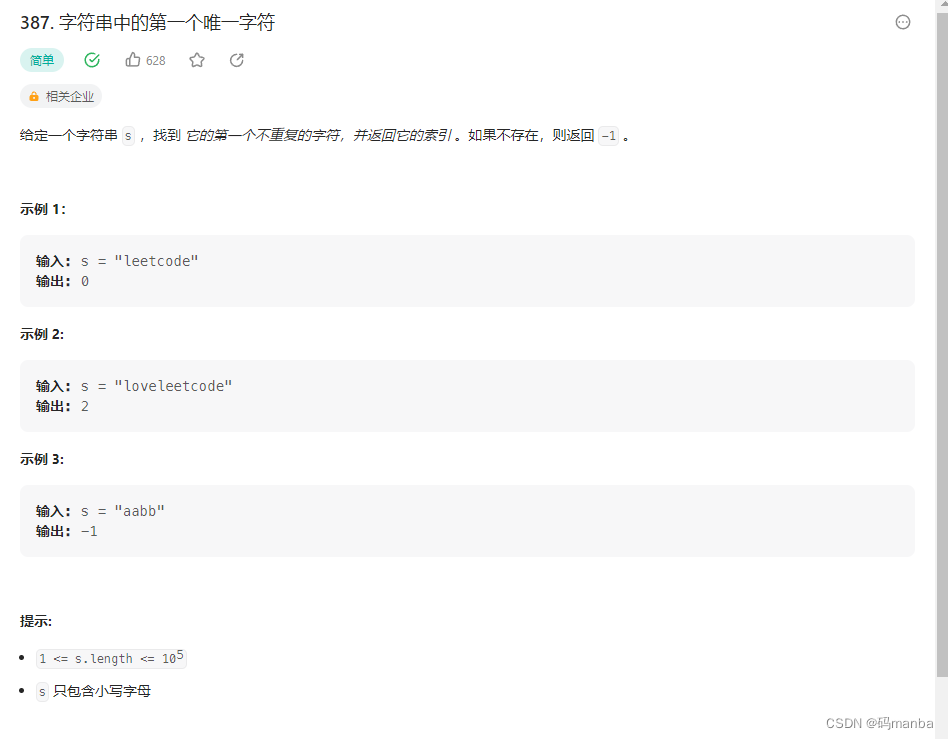
思路
// 两次遍历
// 第一次遍历用哈希表纪录出现的字母频次
// 第二次遍历判断一次频次的字母,返回其下标
代码
class Solution {
public int firstUniqChar(String s) {
// 两次遍历
// 第一次遍历用哈希表纪录出现的字母频次
// 第二次遍历判断一次频次的字母,返回其下标
HashMap<Character, Integer> map = new HashMap<>();
// 第一次遍历,统计频次
for(int i=0; i<s.length(); i++) {
char el = s.charAt(i);
map.put(el, map.getOrDefault(el, 0)+1);
}
// 第二次遍历, 判断
for(int i=0; i<s.length(); i++) {
char el = s.charAt(i);
if(map.get(el) == 1) {
return i;
}
}
// 如果没有出现频次为1的则说明全有重复
return -1;
}
}
383. 赎金信
问题
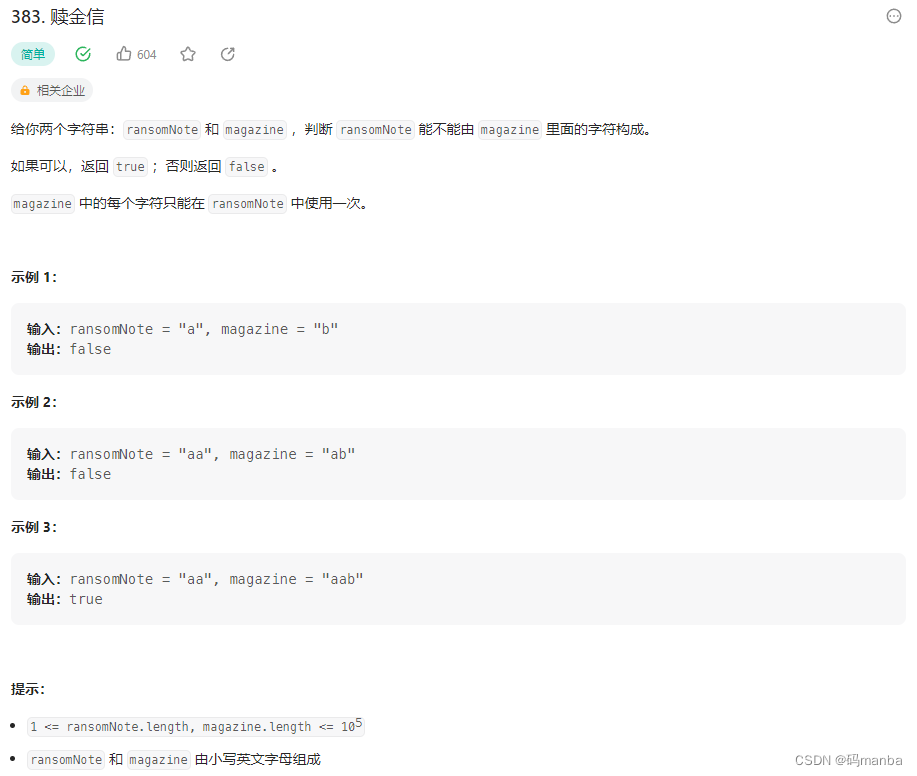
·思路
统计 两个字符串的字符出现的次数, 再比较字符串1出现的字符次数是否小于字符串2出现的次数
全部小于则,字符串1可由字符串2组成
代码
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
/**
统计 两个字符串的字符出现的次数, 再比较字符串1出现的字符次数是否小于字符串2出现的次数
全部小于则,字符串1可由字符串2组成
*/
HashMap<Character, Integer> map1 = new HashMap<>();
HashMap<Character, Integer> map2 = new HashMap<>();
// 统计字符串1的字符个数
for(int i=0; i<ransomNote.length(); i++) {
char el = ransomNote.charAt(i);
map1.put(el, map1.getOrDefault(el, 0) + 1);
}
// 统计字符串2的字符个数
for(int i=0; i<magazine.length(); i++) {
char el = magazine.charAt(i);
map2.put(el, map2.getOrDefault(el, 0) + 1);
}
// 比较第一个字符串出现的字符是否都小于第二个字符串的字符数
for(char key: map1.keySet()) {
if(map1.get(key) > map2.getOrDefault(key, 0)) {
return false;
}
}
// 全部满足时会到这里
return true;
}
}
242. 有效的字母异位词
问题
思想
用map分别统计两个字符串出现的字符的次数
第一个字符串出现时频率加1
第二个字符串出现时频率减1
最后看频率是否全为0
代码
class Solution {
public boolean isAnagram(String s, String t) {
/**
用map分别统计两个字符串出现的字符的次数
第一个字符串出现时频率加1
第二个字符串出现时频率减1
最后看频率是否全为0
*/
// 创建两个map,用于统计字符出现的频次
HashMap<Character, Integer> map = new HashMap<>();
// 统计字符串1的字符出现频率(出现加一)
for(int i=0; i<s.length(); i++) {
char el = s.charAt(i);
map.put(el, map.getOrDefault(el, 0) + 1);
}
// 统计字符串2的字符出现频率(出现减一)
for(int i=0; i<t.length(); i++) {
char el = t.charAt(i);
map.put(el, map.getOrDefault(el, 0) - 1);
}
// 比较是否相等
for(char key:map.keySet()) {
if(map.get(key) != 0) {
// 存在一个不相等,就不是异位词
return false;
}
}
// 字符个数全相等才是异位词
return true;
}
}
链表
141. 环形链表
问题
思想
- 方法一:就是用快慢指针, 无环的话快指针会先到尾部,有环的话快指针会追上慢指针
- 方法二: 通过一个set集合结构, 如果指针到尾部就无环,如果指针被重复添加到set则有环(add方法添加重复时返回fasle)
快慢指针法
public boolean hasCycle(ListNode head) {
if(head==null || head.next==null) {
// 快慢指针的起始位置为空,一定无环
return false;
}
// 判断链表是否有环,可通过快慢指针
ListNode high,low = new ListNode();
low = head;
high = head.next;
while(low != high) {
// 如果无环,快指针能率先到达尾部
if(high == null || high.next==null) {
// 此时为无环
return false;
}
// 快指针一次后移两位,慢指针一次后移一位
low = low.next;
high = high.next.next;
}
// 快慢指针相等的时候跳出了循环代表有环了
return true;
}
使用set判断是否有重复结点的方法
public boolean hasCycle(ListNode head) {
Set<ListNode> set = new HashSet<>();
while(head!=null) { //head 等于 null 时表示到尾部无环
if(!set.add(head)) {
// 有重复时添加返回false,表示有环, 取反后进入该方法体
return true;
}
head = head.next;
}
// 无环
return false;
}
21. 合并两个有序链表
问题
思想
比较两个链表的值,将较小的结点拿到新的链表,以尾插法的方式进行插入
注意从两个链表拿出结点时的断链操作
代码
class Solution {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
/**
比较两个链表的值,将较小的结点拿到新的链表,以尾插法的方式进行插入
注意从两个链表拿出结点时的断链操作
*/
// list 为最终链表表头, l1,l2用于暂存list1/2, r为新链表的尾指针
ListNode l1,l2,r = new ListNode();
l1 = list1;
l2 = list2;
ListNode list = new ListNode();
r = list;
while(l1!=null && l2 != null) {
if(l1.val < l2.val) {
r.next = l1; // 将l1链接到新链表尾部
l1 = l1.next; // l1后移
}else{
r.next = l2; // 将l2链接到新链表尾部
l2 = l2.next; // l2后移
}
r = r.next; // 新链表尾指针后移
r.next = null; // 断链
}
// 检查还没有遍历完的链表
while(l1!=null) {
r.next = l1;
l1=l1.next;
r = r.next;
r.next=null;
}
while(l2!=null) {
r.next = l2;
l2=l2.next;
r = r.next;
r.next=null;
}
// 返回新链表
list = list.next;
return list;
}
}
203. 移除链表元素
问题
思想
通过一个游标遍历链表,当遇到指定删除的值的时候,进行删除操作, 注意一些细节,在代码中有标注
代码
class Solution {
public ListNode removeElements(ListNode head, int val) {
/**
通过一个游标遍历链表,当遇到指定删除的值的时候,进行删除操作
*/
ListNode t = head;
// 头结点为空直接返回
if(head == null) {
return head;
}
while(t.next != null) {
if(t.next.val == val) {
// t.next 为要删除的时 直接删除
t.next = t.next.next;
}else{
// 不为删除时后移
t = t.next;
}
}
// 判断表头是否为要删除
if(head.val == val && head!=null) {
head = head.next;
}
return head;
}
}
206. 反转链表
问题
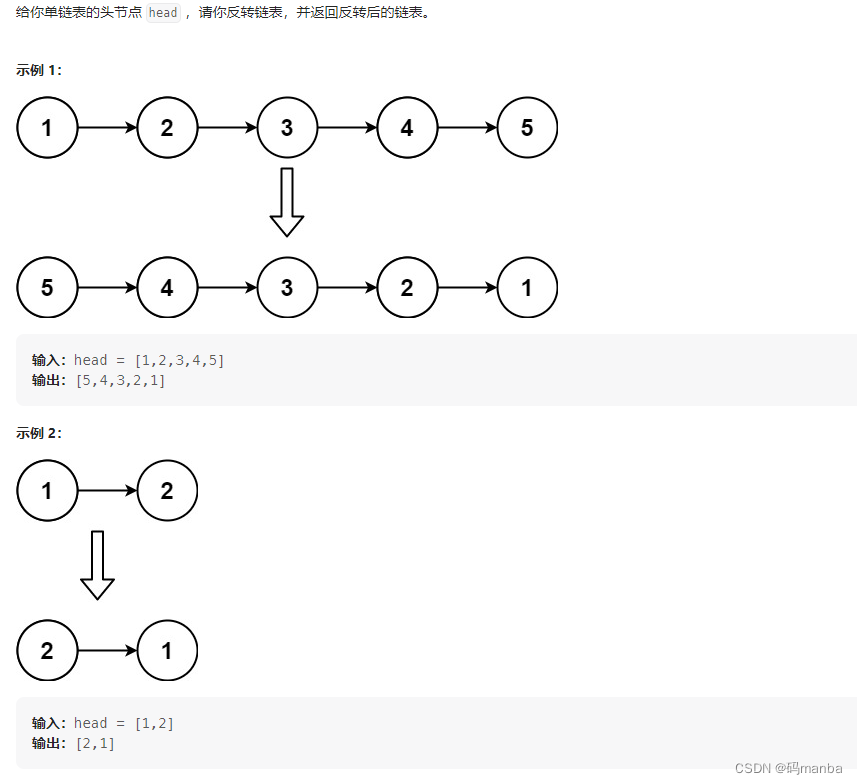
思想
遍历一个遍历,拿到的结点以头插法插入到另一个链表
代码
class Solution {
public ListNode reverseList(ListNode head) {
/**
遍历一个遍历,拿到的结点以头插法插入到另一个链表
*/
// 如果本来就是空
if(head==null) {
return head;
}
// 创建新的链表
ListNode L = head; // 用于保存反转后的链表
ListNode T; // 用于遍历原链表
head = head.next; // 防断链,第一个结点为头结点(本质考察不带头结点的链表反转)
L.next = null; // 断链
while(head!=null) { // 下一个结点不空时
T = head; // 拿到下一个结点
head = head.next; // 防止断链
T.next = L; // 头插法插入新表
L = T;
}
return L;
}
}
83. 删除排序链表中的重复元素
问题
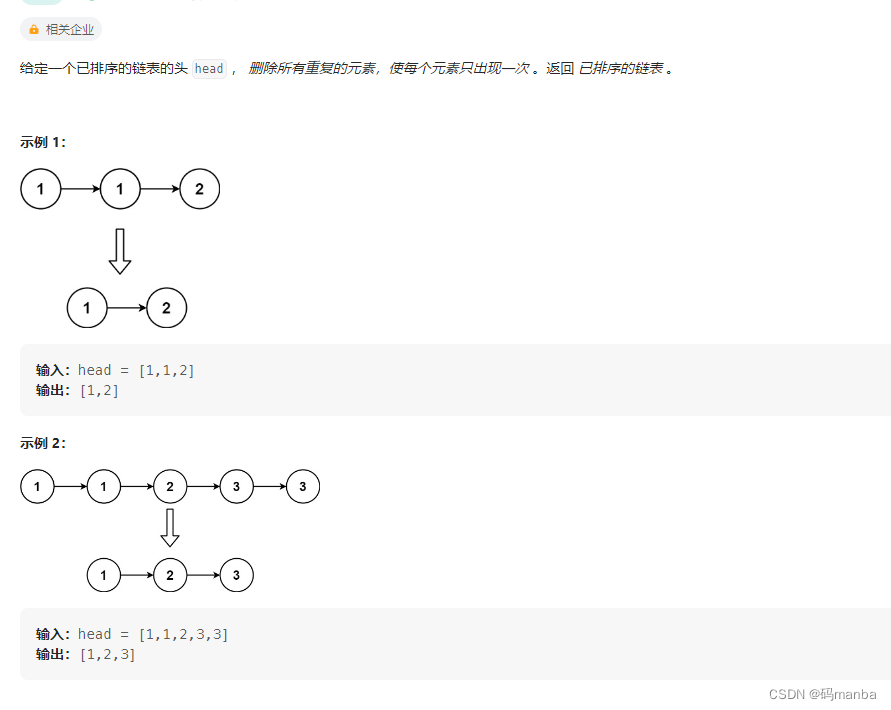
思想
当链表只有一个元素或者空的时候, 直接返回
当链表多余一个元素的时候,比较当前结点与下一个结点是否相同,相同时删除下个结点
代码
class Solution {
public ListNode deleteDuplicates(ListNode head) {
/**
当链表只有一个元素或者空的时候, 直接返回
当链表多余一个元素的时候,比较当前结点与下一个结点是否相同,相同时删除下个结点
*/
if(head==null || head.next==null) {
return head;
}
ListNode L = head;
while(L.next!=null) {
if(L.next.val == L.val) {
// 下一个结点和当前结点相同时
L.next = L.next.next;
}else {
// 不相同时后移
L = L.next;
}
}
return head;
}
}
栈和队列
20. 有效的括号
问题
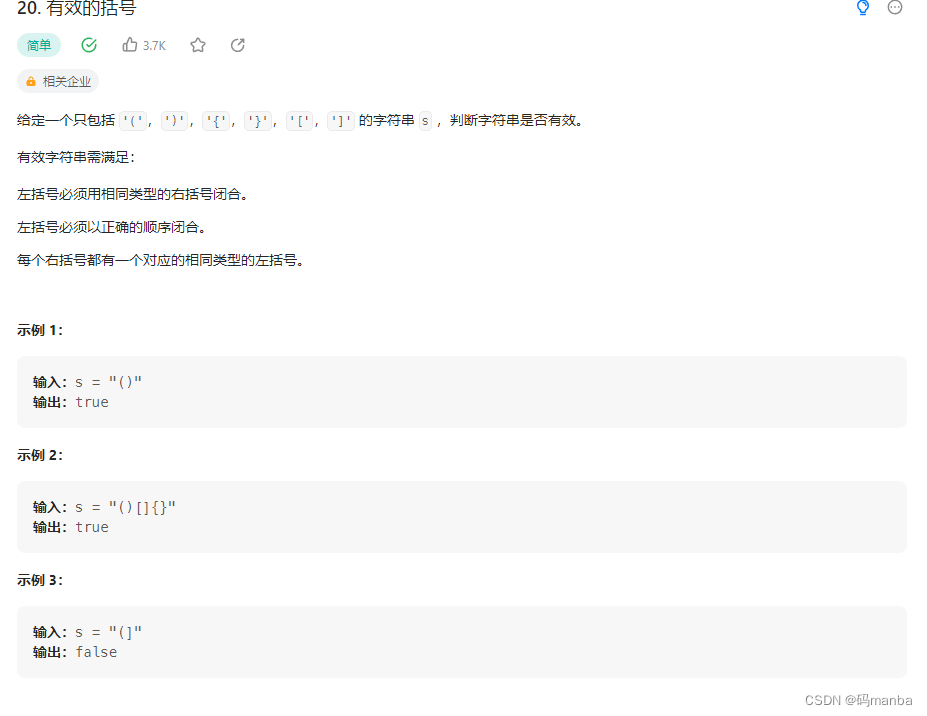
思想
通过栈这个数据结构实现括号匹配,当遇到左括号入栈,遇到右括号出战比对是否对应
当字符串遍历结束时,栈空则匹配成功,栈不空则匹配失败。
代码
class Solution {
public boolean isValid(String s) {
/**
通过栈这个数据结构实现括号匹配,当遇到左括号入栈,遇到右括号出战比对是否对应
当字符串遍历结束时,栈空则匹配成功,栈不空则匹配失败。
*/
// 声明栈
Stack<Character> stack = new Stack<>();
// 遍历字符串
for(int i=0; i<s.length(); i++) {
char el = s.charAt(i);
if(el=='(' || el=='[' || el=='{') {
// 左括号就入栈
stack.push(el);
}else{
if(stack.empty()) {
// 上来就不是左括号,一定不对
return false;
}
char t = stack.pop(); // 栈顶出栈
// 如果是右括号时
if(el==')' && t!='(' ) {
return false;
}
if(el==']' && t!='[') {
return false;
}
if(el=='}' && t!='{') {
return false;
}
}
}
return stack.empty()?true:false;
}
}
232. 用栈实现队列
问题
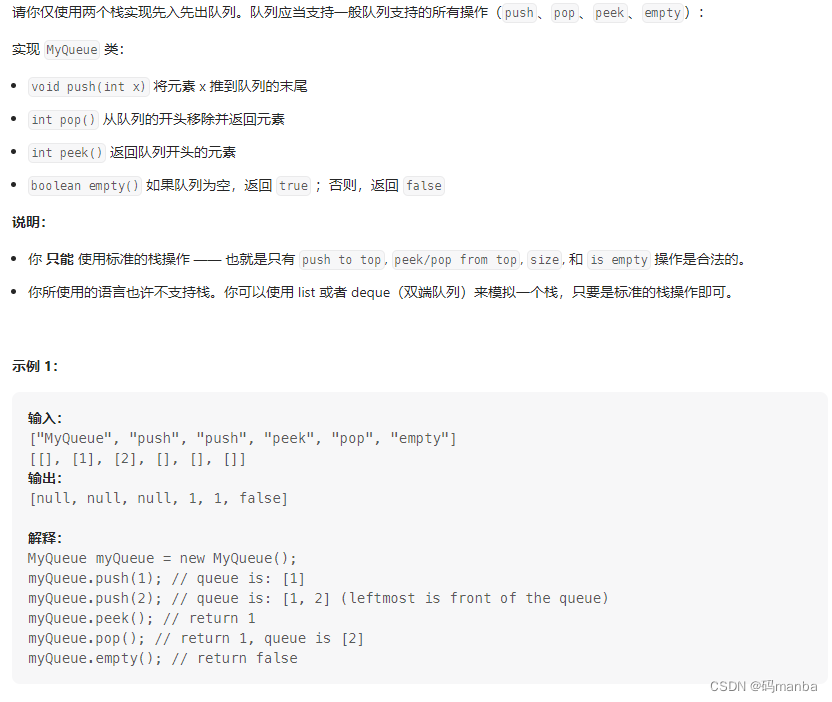
思想
// 两个栈都是无限容量
入队: 往栈1进
队空: 栈1,栈2都空
出队: 栈2有元素,直接出栈2, 无元素时,先把栈1出到栈2,再从栈2出
代码
class MyQueue {
/**
// 两个栈都是无限容量
入队: 往栈1进
队空: 栈1,栈2都空
出队: 栈2有元素,直接出栈2, 无元素时,先把栈1出到栈2,再从栈2出
*/
// 声明两个栈
Stack<Integer> s1, s2;
public MyQueue() {
// 构造函数中初始化
s1 = new Stack<>();
s2 = new Stack<>();
}
public void push(int x) { // 入队操作
// 栈1入队
s1.push(x);
}
public int pop() { // 出队
if(s2.empty()) {
// 栈2空
//先把栈1入到栈2
while(!s1.empty()) {
s2.push(s1.pop());
}
}
// 从栈2出栈(因为栈1出栈 再入栈2 后 就是队列了)
return s2.pop();
}
public int peek() { // 获取对头元素
if(s2.empty()) {
// 栈2空
//先把栈1入到栈2
while(!s1.empty()) {
s2.push(s1.pop());
}
}
// 从栈2出栈(因为栈1出栈 再入栈2 后 就是队列了)
return s2.peek();
}
public boolean empty() { // 判断队空
if(s1.empty() && s2.empty()) {
// 两栈都空则空
return true;
}else {
// 有一栈不空,则不空
return false;
}
}
}
树
144. 二叉树的前序遍历
题目
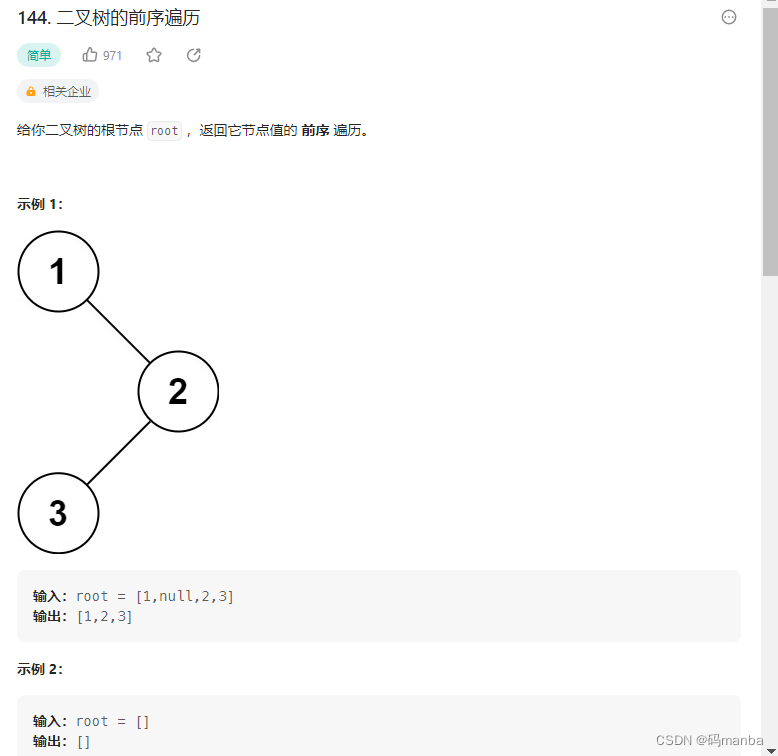
思想
通过递归实现 先序
代码
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
// 创建List
List<Integer> list = new ArrayList<>();
// 调用先序遍历
diGui(root, list);
return list;
}
// 先序
public void diGui(TreeNode T, List<Integer> list) {
// 用于实现递归实现遍历二叉树
if(T==null) {
// 传进结点为空时
return;
}
// 结点不为空
list.add(T.val);
// 遍历左子树
diGui(T.left, list);
// 遍历右子树
diGui(T.right, list);
}
}
94. 二叉树的中序遍历
题目
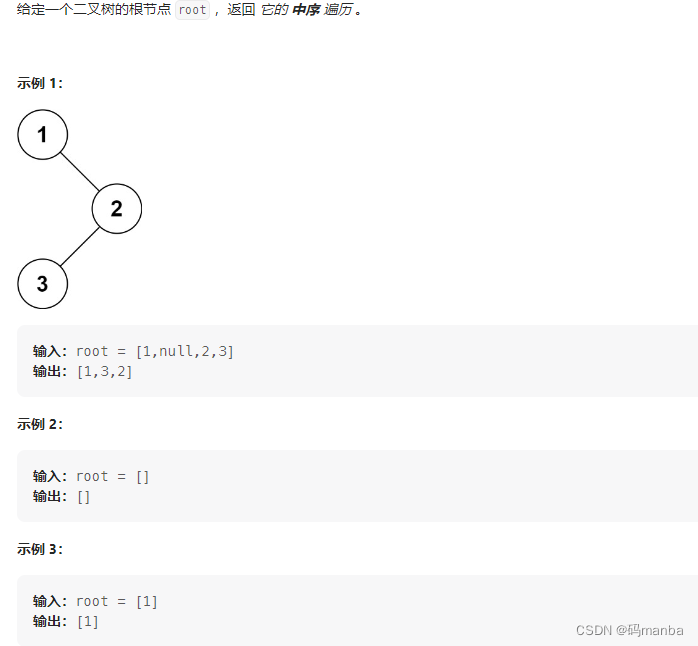
思想
递归实现 中序遍历
代码
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// 创建List
List<Integer> list = new ArrayList<>();
// 调用中序遍历
diGui(root, list);
return list;
}
// 先序
public void diGui(TreeNode T, List<Integer> list) {
// 用于实现递归实现遍历二叉树
if(T==null) {
// 传进结点为空时
return;
}
// 遍历左子树
diGui(T.left, list);
// 结点不为空
list.add(T.val);
// 遍历右子树
diGui(T.right, list);
}
}
145. 二叉树的后序遍历
问题

思想
用递归实现 后序
代码
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
// 创建List
List<Integer> list = new ArrayList<>();
// 调用中序遍历
diGui(root, list);
return list;
}
// 先序
public void diGui(TreeNode T, List<Integer> list) {
// 用于实现递归实现遍历二叉树
if(T==null) {
// 传进结点为空时
return;
}
// 遍历左子树
diGui(T.left, list);
// 遍历右子树
diGui(T.right, list);
// 结点不为空
list.add(T.val);
}
}
102. 二叉树的层序遍历
题目
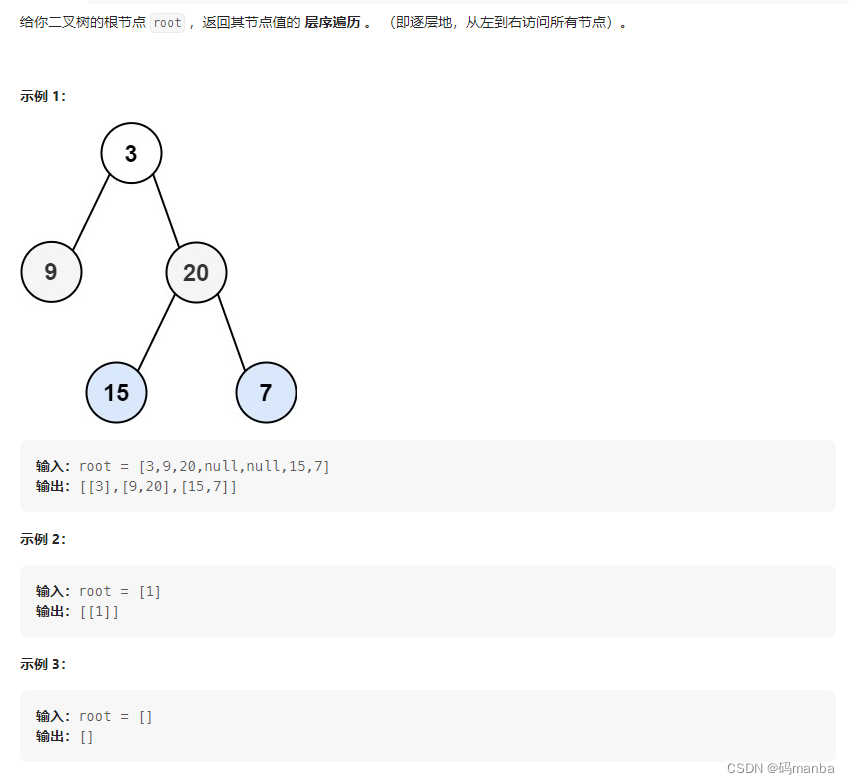
层次遍历实现代码
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
/**
二叉树的层次遍历,通过队列辅助实现
*/
// 创建一个辅助队列
Queue<TreeNode> queue = new ArrayDeque<>();
// 用来保存每层的元素
List<List<Integer>> list = new ArrayList<>();
// 先让根元素入队
if(root==null){ // 根空直接返回
return list;
} else { // 根不空,入队
queue.add(root);
}
while(!queue.isEmpty()) {
// 队列不空时
// 创建每层的List
List<Integer> level = new ArrayList<>();
int n = queue.size(); // 记录当前队列有多少元素,也就是本层多少元素
for(int i=0; i<n; i++) {
TreeNode node = queue.poll(); // 出队
// 将该节点添加到二维列表
level.add(node.val);
// 判断左右指针域是否为空,不空则将结点入队
if(node.left !=null) {
queue.add(node.left);
}
if(node.right != null) {
queue.add(node.right);
}
}
// 将本层入到列表
list.add(level);
}
return list;
}
}
104. 二叉树的最大深度
问题
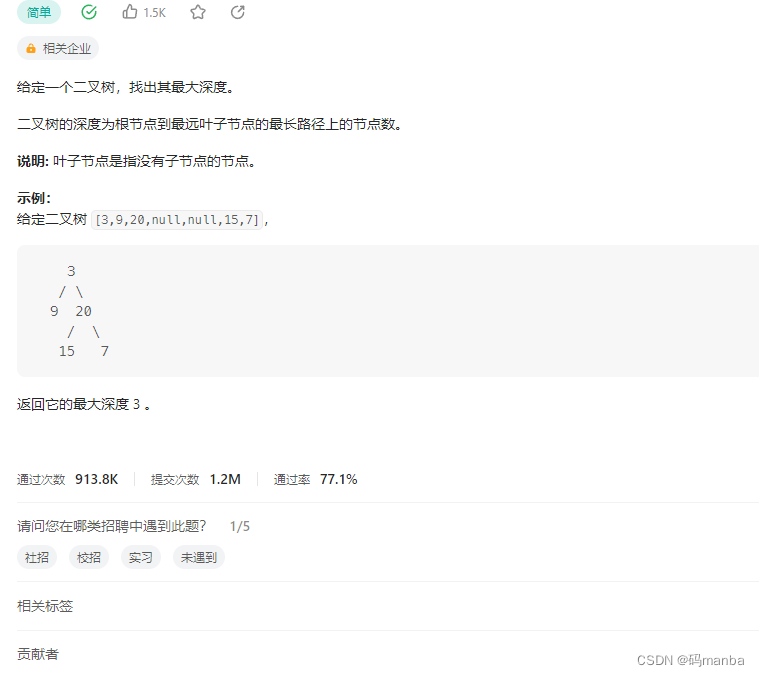
思想
通过递归去做, 当遇到空时返回 0, 非空时 为 左右遍历加1的最大值
代码
class Solution {
public int maxDepth(TreeNode root) {
// 通过递归去做, 当遇到空时返回 0, 非空时 为 左右遍历加1的最大值
if(root == null) {
return 0;
}else {
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}
}
}
101. 对称二叉树
题目
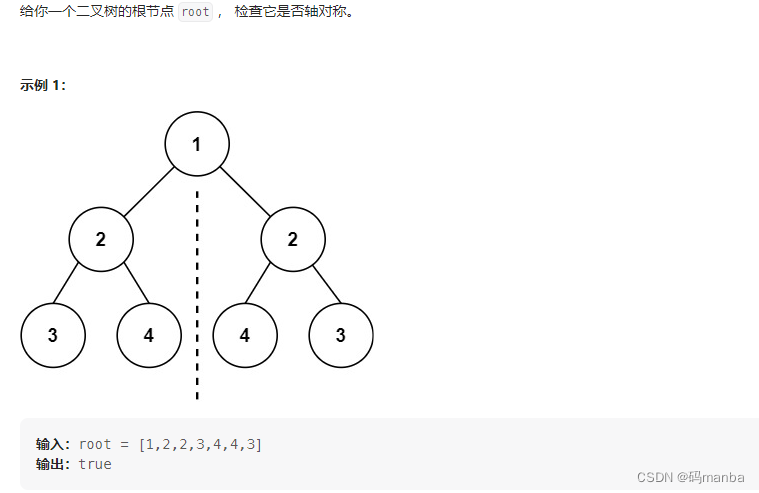
深度优先遍历思想实现代码
class Solution {
public boolean isSymmetric(TreeNode root) {
/**
局部判断, 左有右无/左无右有为不对称
*/
if(root == null) { // 空树为对称
return true;
}
// 如果不是空树,则左右局部递归判断
return dfs(root.left, root.right);
}
public boolean dfs(TreeNode left, TreeNode right) {
if(left==null && right==null) { // 结点的左右都空对称
return true;
}
if(left==null || right==null){ // 存在一面不空,一面空, 不对称
return false;
}
if(left.val != right.val) { // 两边都不空,但是 val不等也不行
return false;
}
// 左右结点都有且 val相同
// 再向下比较, 注意左子树的左孩子要和右子树的右孩子比较
// 左子树的右子孩子要和右子树的左孩子比较
return dfs(left.left,right.right) && dfs(left.right, right.left);
}
}
226. 翻转二叉树
问题
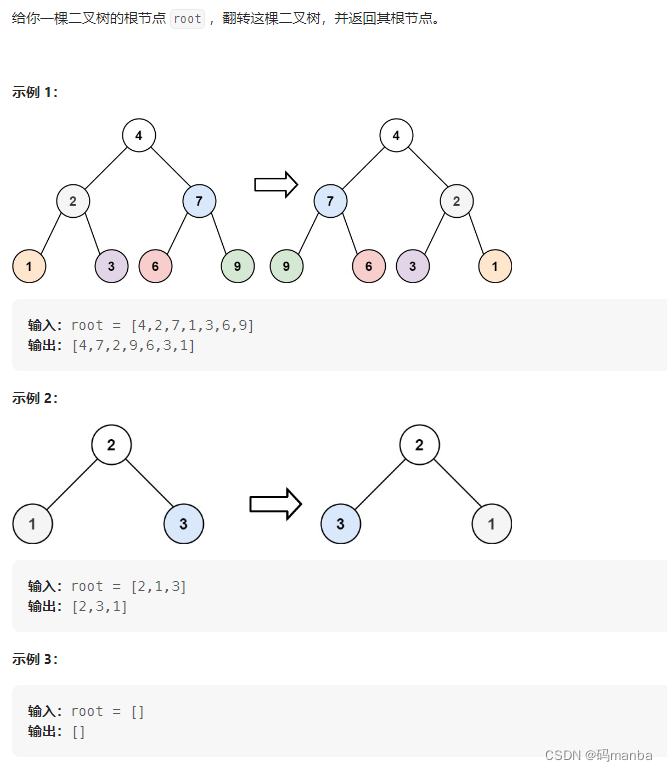
思想
可以通过先序遍历二叉树,对于每个遍历的结点,局部交换左右子树,每个结点都遍历过来的时候,整个树就交换了。
代码
class Solution {
public TreeNode invertTree(TreeNode root) {
diGui(root);
return root;
}
// 遍历交换每个结点的左右子树 (先序)
public void diGui(TreeNode root) {
if(root!=null) {
// 交换左右子树
TreeNode T = root.left;
root.left = root.right;
root.right = T;
// 遍历左子树
diGui(root.left);
// 遍历右子树
diGui(root.right);
}
}
}
112. 路径总和
问题
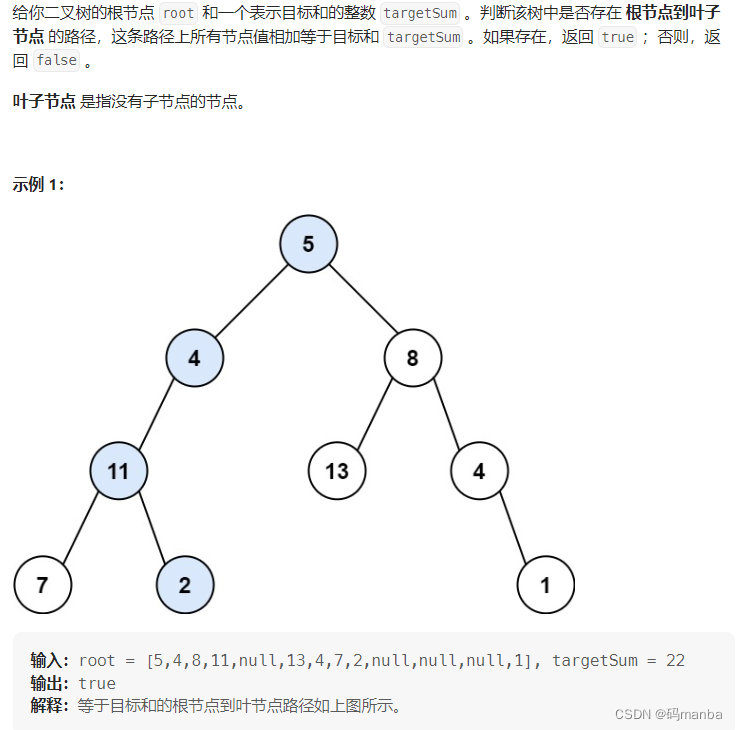
思想
用广度优先遍历, 遍历到每个结点时记录到每个结点的路径长度
通过队列广度优先时,一定是父节点遍历出子节点,所以可以统计到
父节点到字节的的路径
代码
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
/**
思路1: 用广度优先遍历, 遍历到每个结点时记录到每个结点的路径长度
通过队列广度优先时,一定是父节点遍历出子节点,所以可以统计到
父节点到字节的的路径
*/
// 先判断是不是空树
if(root==null) {
return false;
}
// 创建两个辅助队列, 一个记录结点,一个记录元素
Queue<TreeNode> queueNode = new LinkedList<>();
Queue<Integer> queueInt = new LinkedList<>();
// 根结点入队
queueNode.offer(root);
queueInt.offer(root.val);
while(!queueNode.isEmpty()) {
TreeNode now = queueNode.poll();
int temp = queueInt.poll();
// 假如该出队结点为叶子,判断到该出队的结点的路径和是不是等于目标值
if(now.left==null && now.right==null) {
if(temp == targetSum) {
// 到叶子结点等于模板值
return true;
}
// 否则就跳过此循环
continue;
}
// 假如不是叶子结点,则将存在的孩子结点入队
if(now.left!=null) { // 左孩子不空
queueNode.offer(now.left);
queueInt.offer(now.left.val + temp); //父节点值加左孩子结点值
}
if(now.right != null) { // 右孩子不空
queueNode.offer(now.right);
queueInt.offer(now.right.val + temp); // 父节点加左节点的值
}
}
return false;
}
}
700. 二叉搜索树中的搜索
问题
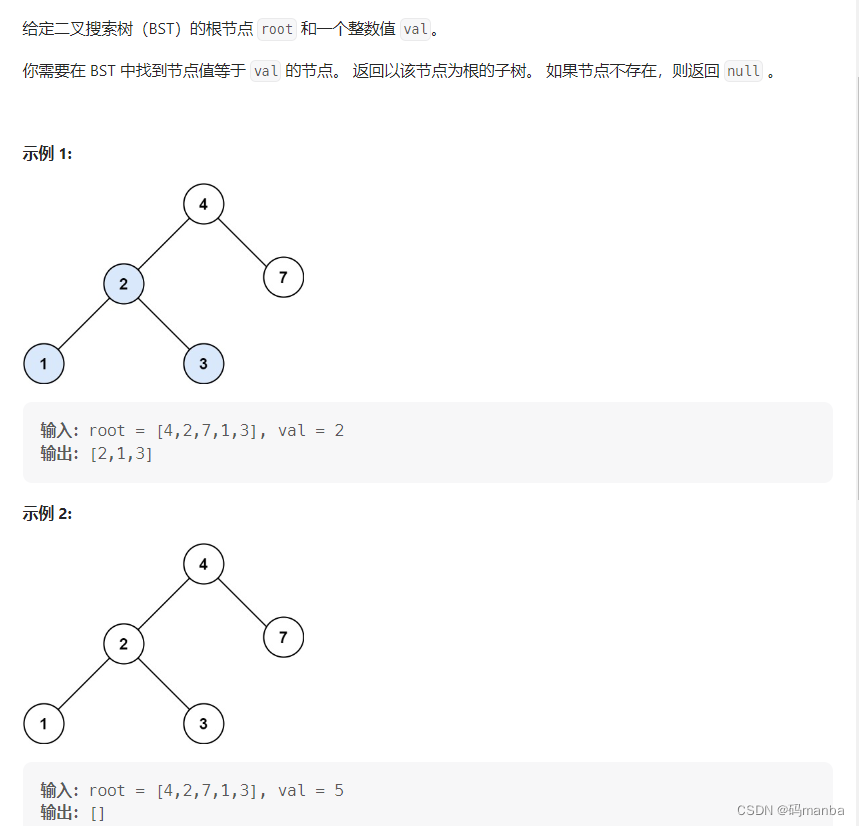
思想
// 通过先序遍历,遍历二叉树,然后访问结点的时候看是否等于val,等于则返回该结点,
// 不等于则看结点值大于还是小于根结点,大于根结点则在右子树,小于则在左子树
代码
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
// 通过先序遍历,遍历二叉树,然后访问结点的时候看是否等于val,等于则返回该结点,
// 不等于则看结点值大于还是小于根结点,大于根结点则在右子树,小于则在左子树
if(root == null) {
return null;
}else if(root.val == val){ // 找到结点
return root;
}else if(root.val < val){
// 根小,向右寻找
return searchBST(root.right, val);
}else {
// 根大,向左寻找
return searchBST(root.left, val);
}
}
}
701. 二叉搜索树中的插入操作
问题
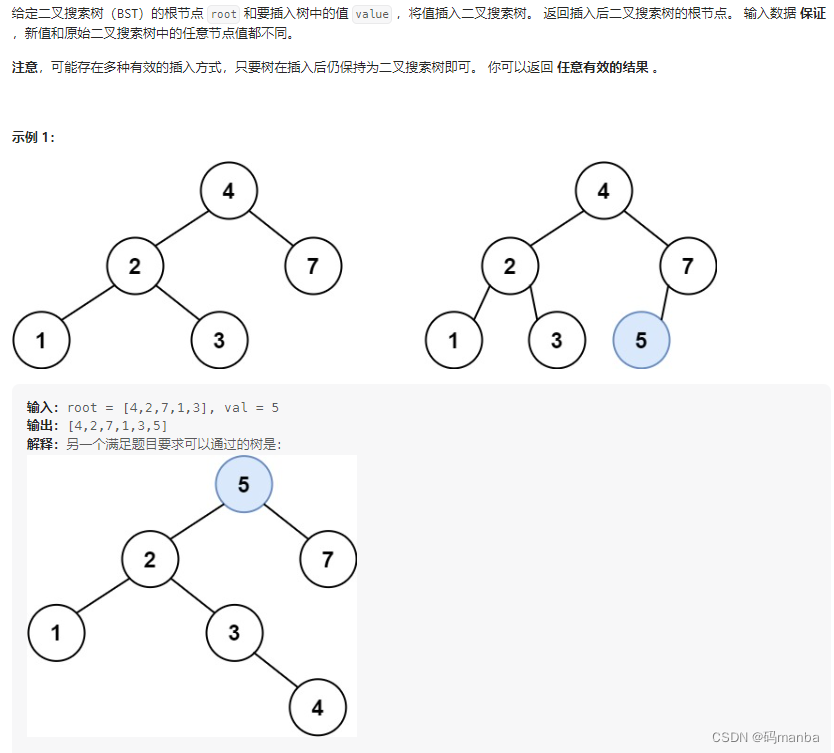
思想
通过二叉搜索树的思想,找到叶子结点判断插入到叶子结点的左孩子或者右孩子上
代码
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
// 通过二叉搜索数的方式
if(root == null) {
return new TreeNode(val);
}else {
// 如果没有到null,就按二叉搜索树去寻找
if(root.val > val) {
// 根大,在左侧
root.left = insertIntoBST(root.left, val);
}else {
// 传入规则没有相等值,则为根小在右侧
root.right = insertIntoBST(root.right, val);
}
}
return root;
}
}
98. 验证二叉搜索树
问题
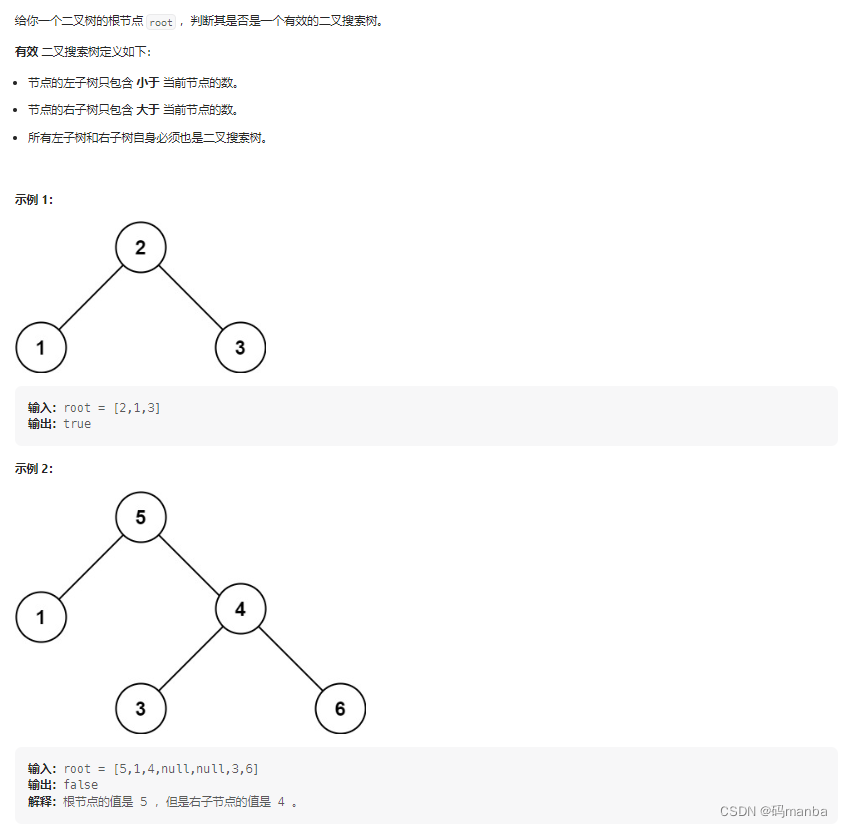
思路
/**
方案1: 采用递归判断的方式
1. 首先我们知道bsf每个结点的左子树全小于它,右子树全大于它,每个结点都是如此
2. 我们用一个low,high记录到当前结点的值,当前结点作为父节点时
其左子树皆小于它,所以该结点的值作为向左遍历的上限值
其右子树皆大于它,所以该结点的值作为向右遍历的下限值
3. 所以当遍历到一个结点时会判断该结点的值
是不是小于最小值(因为最小值向右遍历确定的,右子树皆大于父节点,所以有小于最小值的不为二叉搜索树)
或是否大于最大值(同理更新最大值是向左遍历时确定的,所以当前结点大于最大值时,不为bsf)
*/
·代码
class Solution {
public boolean isValidBST(TreeNode root) {
return bsf(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean bsf(TreeNode root, long low, long high) {
if(root==null) {
return true;
}else if(root.val >=high || root.val<=low) { // 在子树中有超过父节点的值或者低于
return false;
}else { // 向左遍历时更新上限,向右遍历时更新下限
return bsf(root.left, low, root.val) && bsf(root.right,root.val, high);
}
}
}
653. 两数之和 IV - 输入二叉搜索树
问题
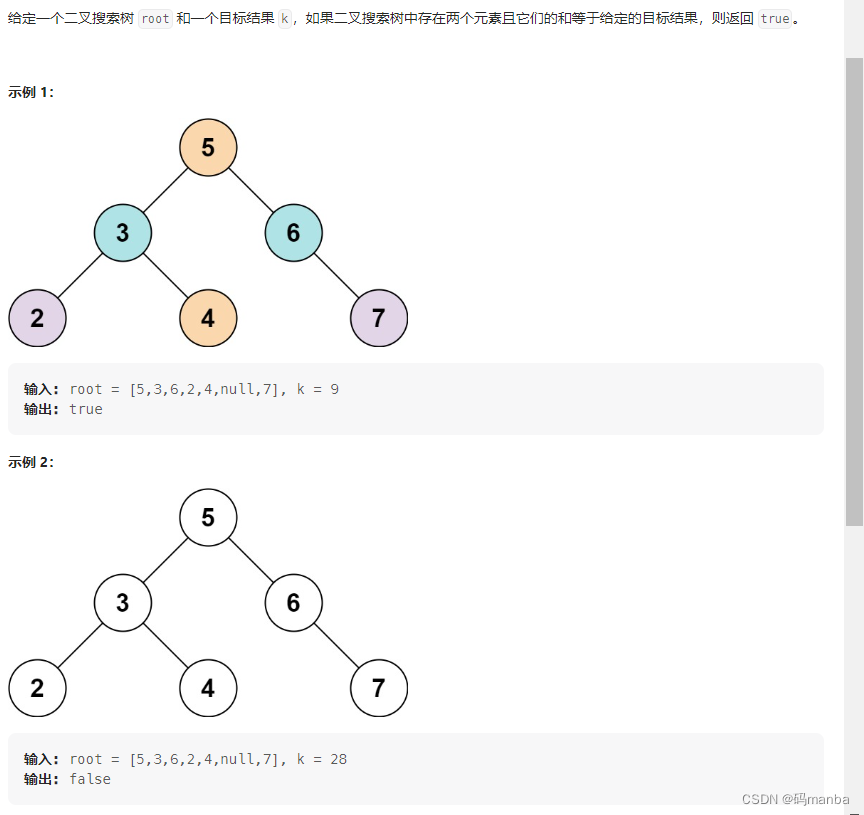
思路·
/**
通过集合的判断有没有符合 k-当前结点值 得值在集合中
每次都将遍历到的结点值加入到集合当中,当bsf中存在两个结点的值等于目标值的时候
当遍历到第二个加和的值的时候在集合中一定有 k-当前结点的值
*/
代码
class Solution {
Set<Integer> set = new HashSet<Integer>();
public boolean findTarget(TreeNode root, int k) {
/**
通过集合的判断有没有符合 k-当前结点值 得值在集合中
每次都将遍历到的结点值加入到集合当中,当bsf中存在两个结点的值等于目标值的时候
当遍历到第二个加和的值的时候在集合中一定有 k-当前结点的值
*/
if(root == null) {
return false;
}
if(set.contains(k - root.val)) {
// 集合中存在 一个值为 目标值减去当前结点值 == 有两个值加起来等于目标结点值
return true;
}
set.add(root.val);
return findTarget(root.left, k) || findTarget(root.right, k);
}
}
235. 二叉搜索树的最近公共祖先
问题

代码
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) {
return root;
}
// 开始递归
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
// 如果left为空,说明两个结点都在右子树
if(left == null) {
return right;
}
// 如果right 为空 说明两个结点都在左子树
if(right == null) {
return left;
}
// 如果left和right都不为空,说明这两个结点一个在左子树一个在右子树
return root;
}
}





![MySQL数据库面试题[万字汇总]](https://img-blog.csdnimg.cn/img_convert/f3847a4e31207ee84f5c01dc3a7278ec.png)
![流批一体计算引擎-5-[Flink]的Python Table API和SQL程序](https://img-blog.csdnimg.cn/21ba496b1beb42a5b92d6e10a6236641.png)