LeetCode 437. 路径总和 III

  

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

  

示例 1：

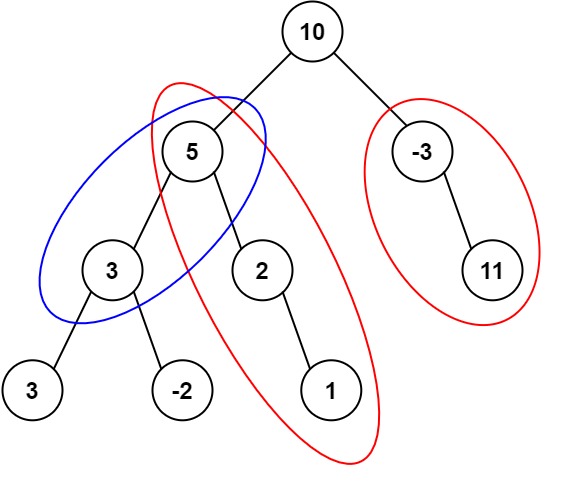
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

• 二叉树的节点个数的范围是 [0,1000]
• -109 <= Node.val <= 109 
• -1000 <= targetSum <= 1000 

思路：

dfs递归，将每个节点都当做起始的根节点对待

• 该题可以通过在子函数中增加额外入参 【sum累加和】来做加法，通过比较【当前累加和】是否和【目标和】相等： if sum + node.Val == targetSum
• 也可以通过对已有入参 targetSum做减法，来比较【当前节点值】是否和【不断消减的目标和】相等： if node.Val == target

注意：处理中间层逻辑时，即使找到了一条目标路径，也不立即 return，继续找。因为 Node.val 有可能为负数，后续有可能再减为目标和 targetSum。

时间复杂度：

O(N^2)，其中 N 为该二叉树节点的个数。对于每一个节点，求以该节点为起点的路径数目时，则需要遍历以该节点为根节点的子树的所有节点，因此求该路径所花费的最大时间为 O(N)，我们会对每个节点都求一次以该节点为起点的路径数目，因此时间复杂度为 O(N^2)

空间复杂度： 

O(N)，考虑到递归需要在栈上开辟空间。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */

// 参考：https://leetcode.cn/problems/path-sum-iii/solutions/109711/custerxue-xi-bi-ji-er-cha-shu-de-di-gui-he-dfs-by-/?languageTags=golang
/***************************** 方法1 通过sum额外入参做加法 *****************************/
// 写法1：因为后续的测试用例会覆盖之前的结果，所以这里的res不能在_pathSum初始化，需要在pathSum中初始化
var res int

func pathSum(root *TreeNode, targetSum int) int {
    res = 0 // 多个测试用例下，避免结果被后续测试用例的结果覆盖
    _pathSum(root, targetSum, 0)
    return res
}

func _pathSum(root *TreeNode, targetSum, sum int) {
    if root == nil {
        return
    }

    dfs(root, targetSum, sum)
    _pathSum(root.Left, targetSum, sum)
    _pathSum(root.Right, targetSum, sum)
}

func dfs(node *TreeNode, targetSum, sum int) {
    if node == nil {
        return
    }

    sum += node.Val
    if sum == targetSum {
        res++
    }

    dfs(node.Left, targetSum, sum)
    dfs(node.Right, targetSum, sum)
}


// 写法2：不另外添加_pathSum方法调用，但是dfs中就需要将cnt结果返回才行
var res int

func pathSum(root *TreeNode, targetSum int) int {
    res = 0 // 多个测试用例下，避免结果被后续测试用例的结果覆盖
    if root == nil {
        return 0
    }
    
    return dfs(root, targetSum, 0) + pathSum(root.Left, targetSum) + pathSum(root.Right, targetSum)
}

func dfs(node *TreeNode, targetSum, sum int) int {
    if node == nil {
        return 0
    }

    sum += node.Val
    if sum == targetSum {
        res++
    }

    dfs(node.Left, targetSum, sum)
    dfs(node.Right, targetSum, sum)

    return res
}




/***************************** 方法2 通过targetSum入参做减法 *****************************/
// 写法3：因为后续的测试用例会覆盖之前的结果，所以这里的res不能在_pathSum初始化，需要在pathSum中初始化
var res int

func pathSum(root *TreeNode, targetSum int) int {
    res = 0
    _pathSum(root, targetSum)
    return res
}

func _pathSum(root *TreeNode, targetSum int) int {
    // res = 0
    if root == nil {
        return 0
    }
    
    dfs(root, targetSum)
    _pathSum(root.Left, targetSum) // 分别以root的左右孩子节点为根节点，并不断的继续下探
    _pathSum(root.Right, targetSum)

    return res
}

func dfs(node *TreeNode, target int) {
    if node == nil {
        return
    }
    // 这里因为不限定从根节点到叶节点，所以不需要该条件：if node.Left == nil && node.Right == nil
    if node.Val == target {
        res++
    }

    dfs(node.Left, target - node.Val)
    dfs(node.Right, target - node.Val)
}


// 写法4：不另外添加_pathSum方法调用，但是dfs中就需要将cnt结果返回才行
func pathSum(root *TreeNode, targetSum int) int {
    if root == nil {
        return 0
    }
    
    return dfs(root, targetSum) + pathSum(root.Left, targetSum) + pathSum(root.Right, targetSum)
}

func dfs(node *TreeNode, sum int) int {
    if node == nil {
        return 0
    }

    res := 0
    if node.Val == sum {
        res++
    }

    res += dfs(node.Left, sum - node.Val)
    res += dfs(node.Right, sum - node.Val)
    
    return res
}