深度学习:轻量级神经网络MoblieNet 从v1 到 v2
- MobileNet V1
- 前言
- 深度可分离卷积
- 传统卷积
- Depth Wise Conv
- Point Wise Conv
- 性能对比
- MobileNet V2
- 前言
- 主要改进
- Inverted Residuals Block
- Residual Block
- Expansion Layer
- ReLU6
- Linear Activation Function
- 小结
- 实验
MobileNet V1
前言
MobileNet是谷歌团队在2017年提出的,专注于移动端和嵌入式设备的轻量级CNN网络,相比于传统卷积,相比于传统卷积网络,在准确率小幅降低的情况下大大减少了参数量与运算量。
它的主要贡献就是提出了深度可分离卷积与增加超参数alpha 与 beta。
深度可分离卷积
传统卷积
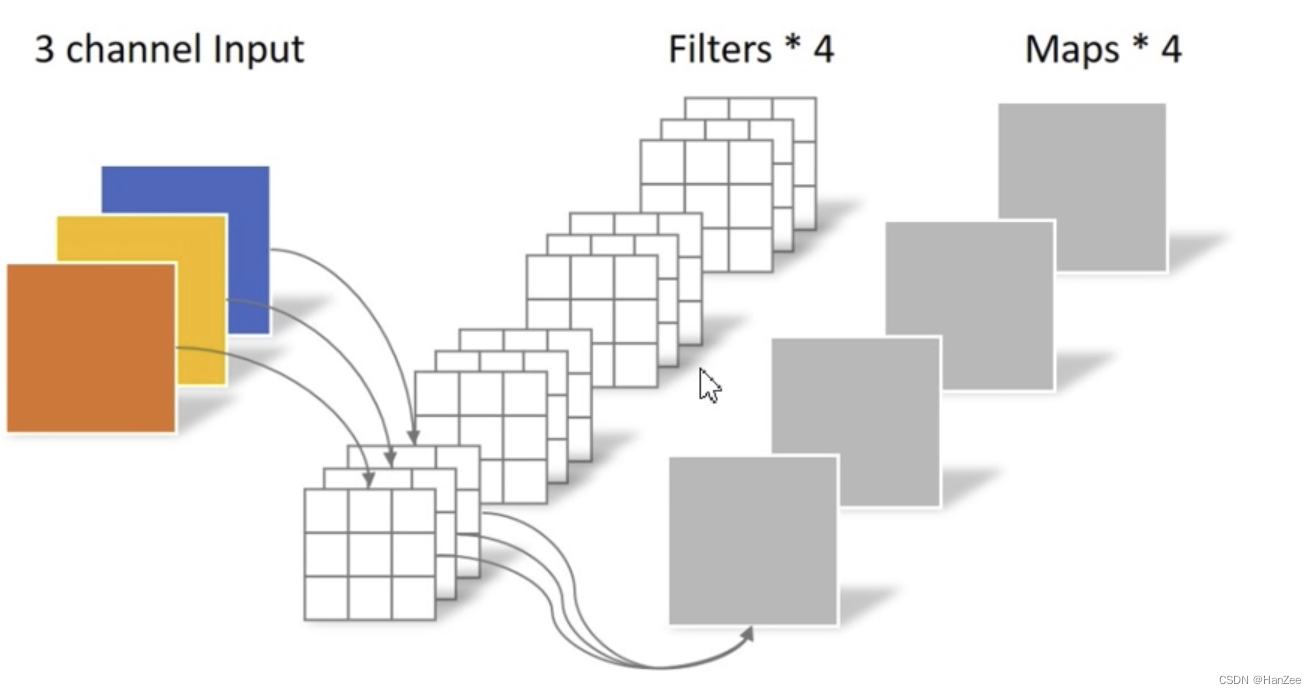
首先我们来回顾一下传统卷积操作如上图,input的channel 为3,那么每个卷积核的channel一定为3,卷积核的数量为4,output 的channel的也一定为4。
对于普通的卷积操作,它既可以融合每个平面(平面指HW维度)的特征也可以融合channel的特征。
Depth Wise Conv
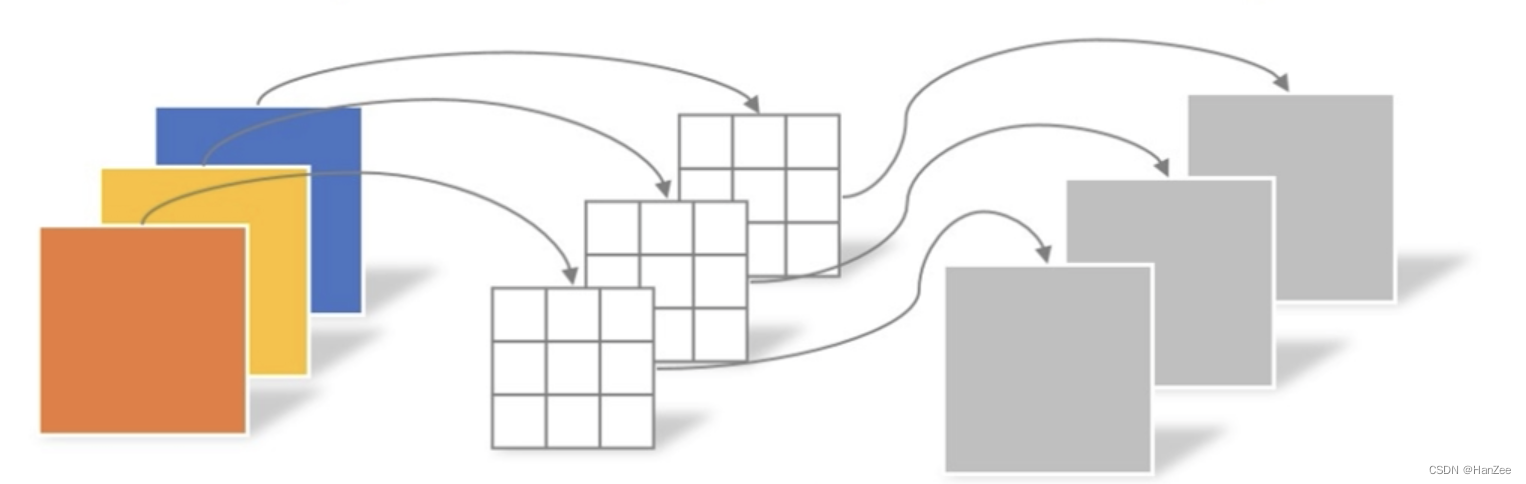
接下来介绍DW卷积,这里input channel还是为3,但是每个卷积核的channel变成了1,只负责input 的一个 channel(以前每个卷积核的channel与input channel一致),这样卷积操作过后就只融合了平面的特征,而没有融合channel特征。
Point Wise Conv
为了弥补空间特征,作者在depth wise conv 后面加入了 point wise conv,其实他就是传统的卷积操作,只不过 kernel size 为 1,那么他就会只融合了channel特征。
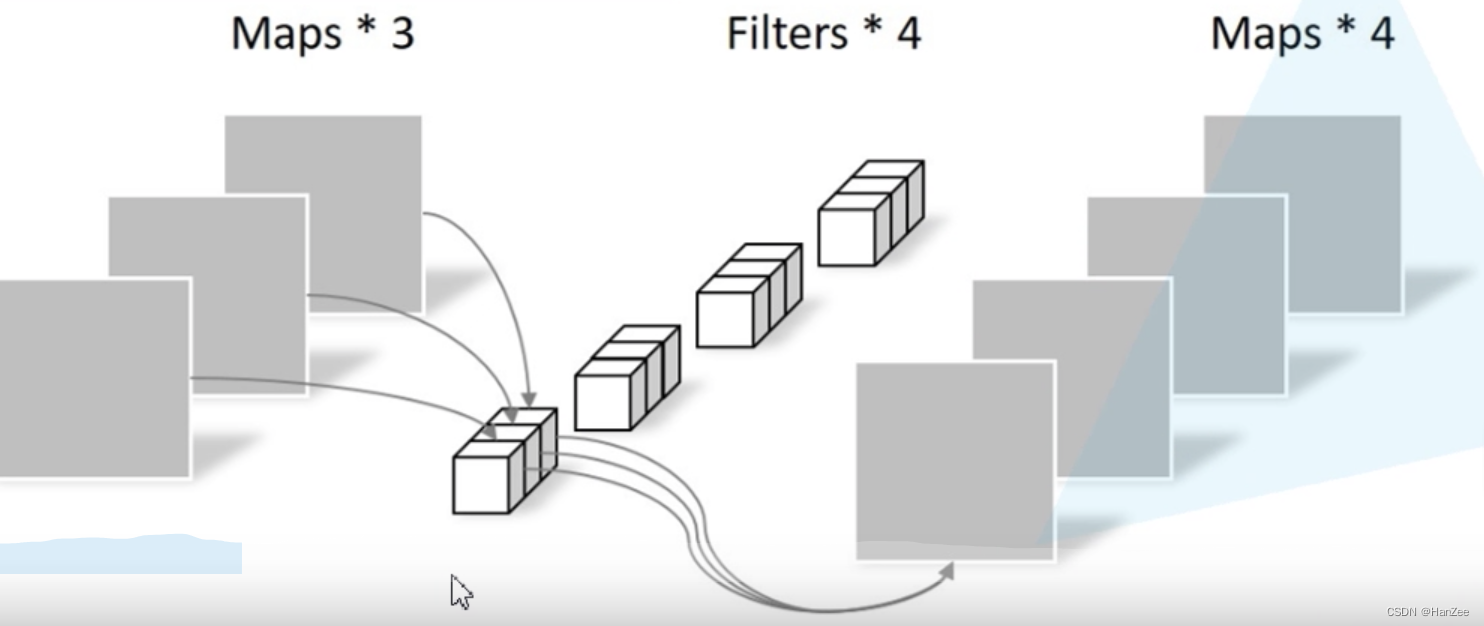
性能对比

这里作者把深度可分离卷积分为 DW + PW,下面我们来比较一下它们的计算量:

在这里 Dk代表kernel size ,DF代表feature map的 H or W, M为input channel N为卷积核数量。
MobileNet V2
前言
MobileNet V2 是谷歌团队2018年提出的网络,相比于MobileNet V1。
主要改进
Inverted Residuals Block
Residual Block
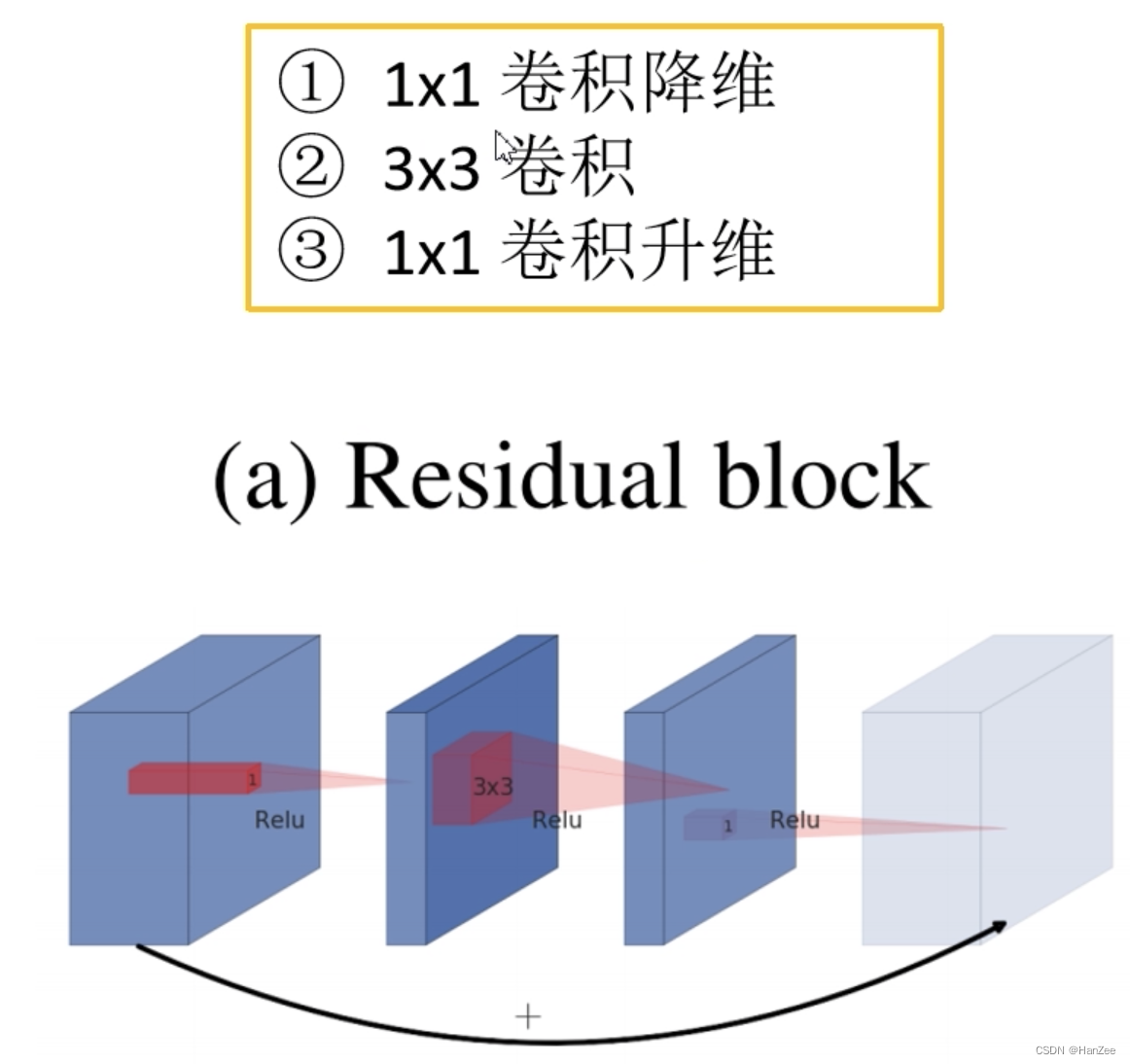
首先我们回顾传统的残差块,它是由一个 1 * 1的卷积降维+ 3 * 3 卷积 + 1* 1卷积升维。(激活函数与BN省略)
Expansion Layer
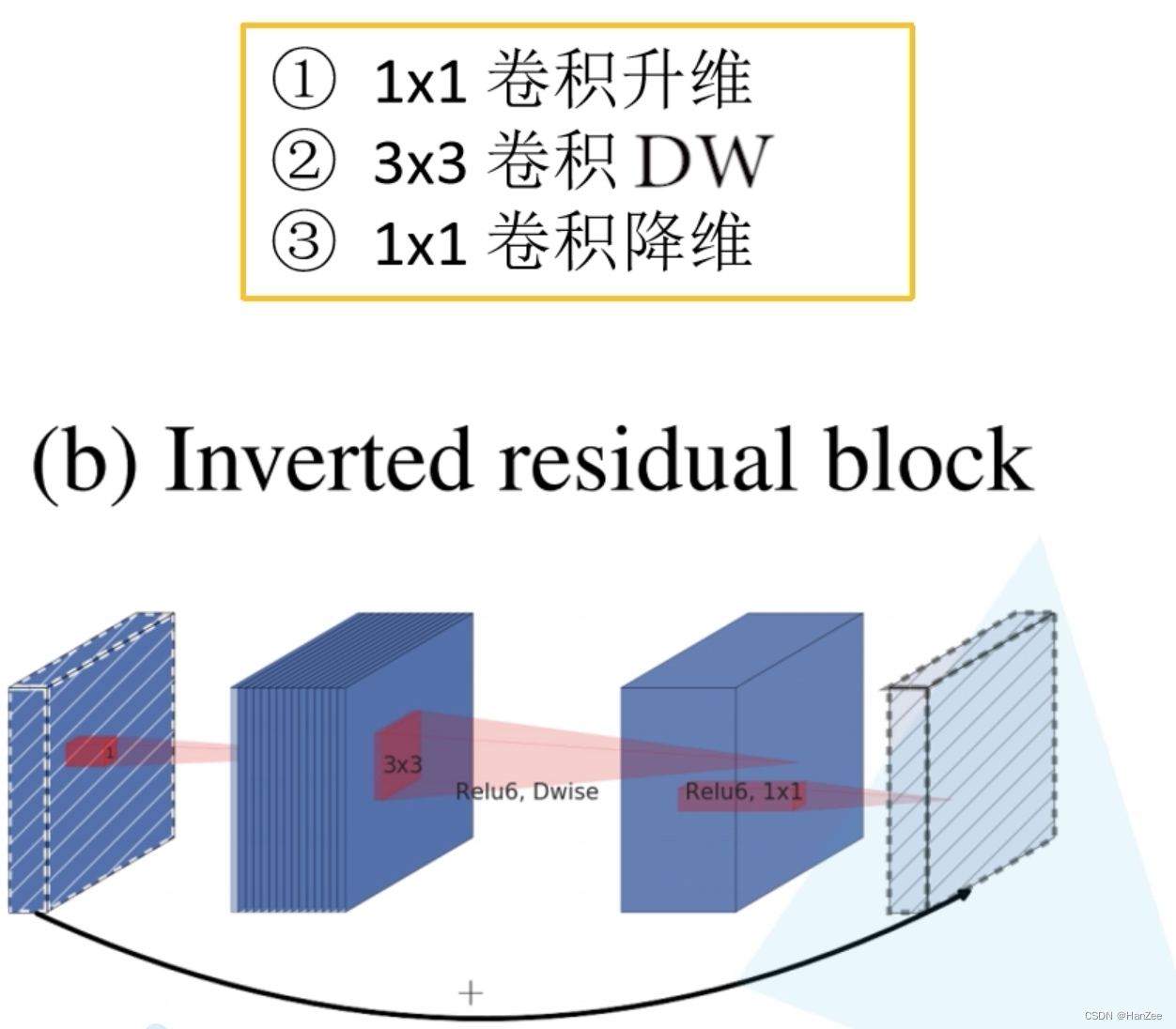
倒残差结构如上图,他是先用 1 * 1卷积升维+DW卷积 + 1* 1卷积降维。
ReLU6
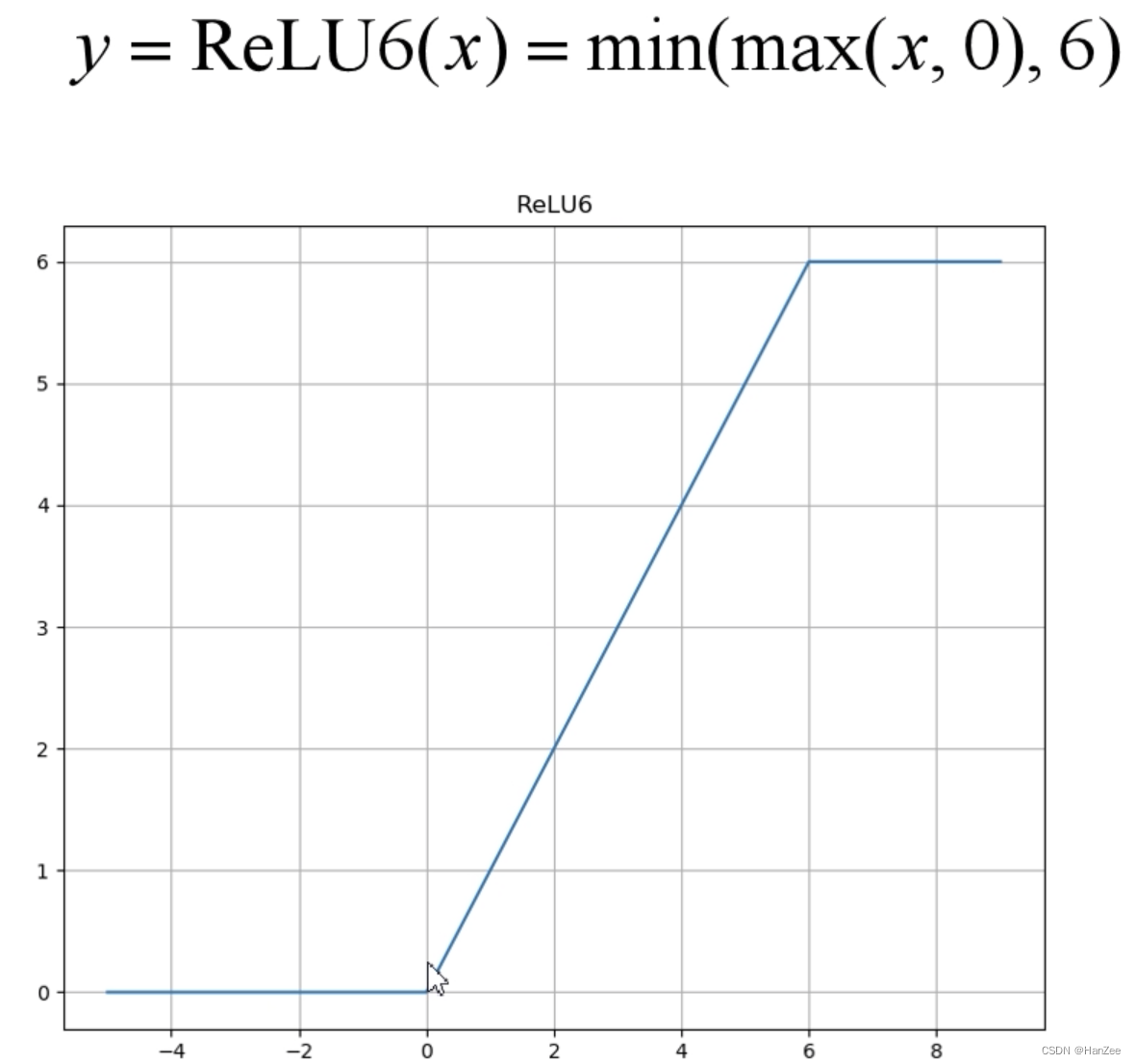
作者把ReLU激活函数换成了ReLU6,y的数值不在随着x的增长而增长,到6之后不再变化。
原因:
由于ReLU的值域是0到正无穷,在低精度浮点数下不能很好的表示,于是改成了ReLU6可以增加模型的稳定性。
这里所说的“低精度”,我看到有人说不是指的float16,而是指的定点运算(fixed-point arithmetic)。
Linear Activation Function
作者通过证明,对低维度做ReLU运算,很容易造成信息的丢失。而在高维度进行ReLU运算的话,信息的丢失则会很少。
所以作者把最后1 * 1卷积降维后的激活函数换成线性激活函数。
小结
把上面内容汇聚到一起,于是就有了如下模块:
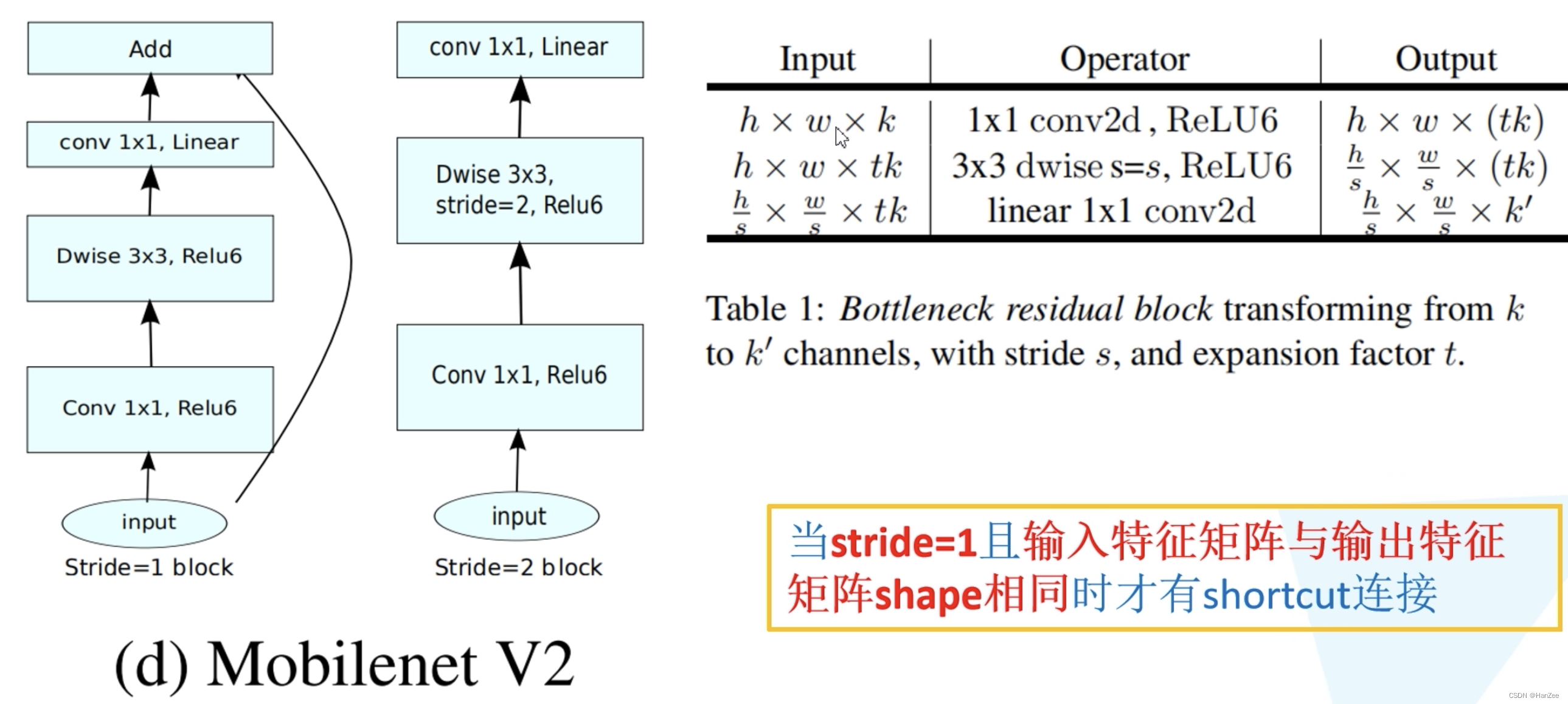
这里注意只有stride =1 的时候才有残差模块,因为要保证输入矩阵特征与输出矩阵特征一致才可以执行add操作。
实验
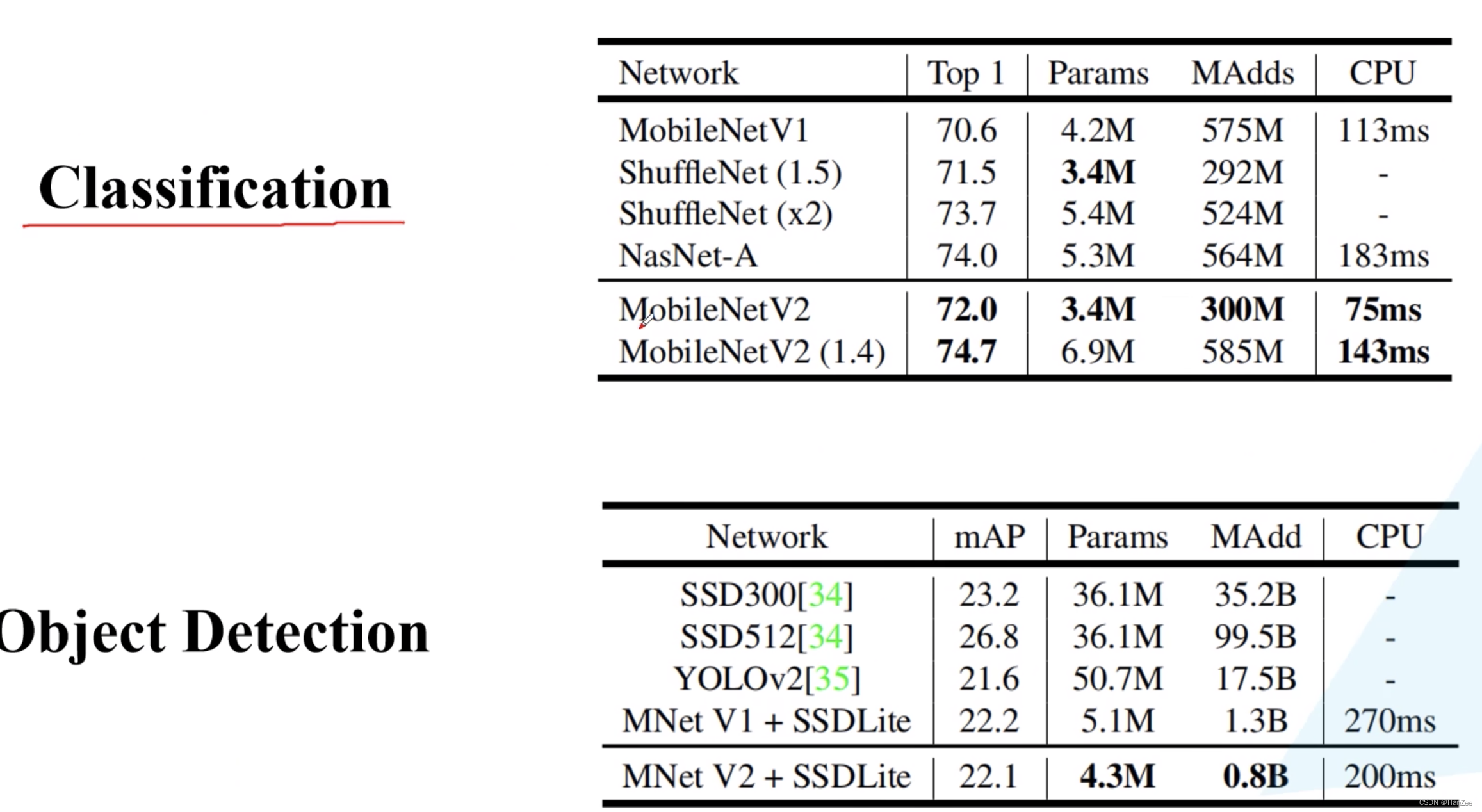











![Introduction to Multi-Armed Bandits——04 Thompson Sampling[2]](https://img-blog.csdnimg.cn/img_convert/c52f2fd8f387c56050a3a2568fe7b273.png)