您的点赞收藏是我继续更新的最大动力!
一定要点击如下的蓝色字体链接，那是获取资料的入口！
点击链接加入群聊【2024国赛资料合集】：http://qm.qq.com/cgi-bin/qm/qr?_wv=1027&k=Ce9u9pqQeBrMHgupi-R078l9TuU0RwSl&authKey=RjsYS3Piiw1bn%2F%2BZagxTvO%2FjCDpTxR57wsd%2Fq%2FMSAaRw%2BFcKLTr5zGraNJzgAAkH&noverify=0&group_code=604186428
http://qm.qq.com/cgi-bin/qm/qr?_wv=1027&k=Ce9u9pqQeBrMHgupi-R078l9TuU0RwSl&authKey=RjsYS3Piiw1bn%2F%2BZagxTvO%2FjCDpTxR57wsd%2Fq%2FMSAaRw%2BFcKLTr5zGraNJzgAAkH&noverify=0&group_code=604186428
现分享下2022年数学建模国赛B题的论文供大家参考学习下：
一、问题重述
1.1 问题背景
由于无人机集群在遂行编队飞行时, 应尽可能的避免外界干扰, 因此需要尽可能的保持电磁静默减少电磁波信号的发射.为保持编队队形, 拟采用纯方位无源定位的方法调整无人机的位置, 即由编队中某几架无人机发射信号, 其余无人机被动接收信号, 从中提取出方向信息进行定位, 来调整无人机的位置.其中, 无人机所接收到的方向信息约定为：该无人机与任意两架发射信号无人机连线之间的夹角.编队中每架无人机均有固定编号, 且在编队中与其他无人机的相对位置关系保持不变.
1.2 问题重述
本文将要解决以下几个问题：
问题一：编队由10架无人机组成, 构成圆形编队, 其中9架无人机均匀分布在某一圆周上, 令一架无人机位于圆心.无人机基于自身感知高度信息, 均保持在同一高度上飞行.建立数学模型, 解决以下问题：
1、 位于圆心的无人机和编队中另2架无人机发射信号, 其余位置略有偏差的无人机被动接收信号.当发射信号的无人机位置无偏差且编号已知时, 建立被动接收信号的无人机的定位模型.
2、某位置略有偏差的无人机接收到编号为FY00和FY01的无人机发射的信号, 另接收到编队中若干编号位置的无人机发射的信号.若发射的无人机位置无偏差, 除FY00和FY01外, 还需要几架无人机发射信号, 才能实现无人机的有效定位?
3、按编队要求, 1架无人机位于圆心, 另外9架无人机均匀分布在半径为100m的圆周上.当初始时刻无人机的位置略有偏差时, 每次选择编号为FY00的无人机和圆周上最多3架无人机遂行发射信号, 其余无人机接收通过多次调整, 最终使9架无人机均匀分布在某个圆周上.其中无人机的初始位置如题所示.
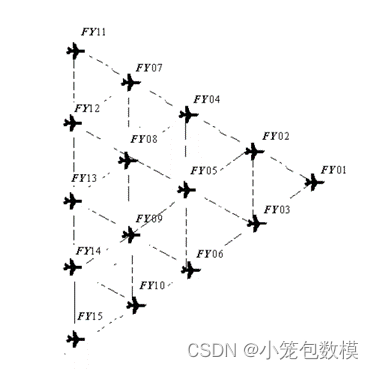
问题二：当无人即集群使其他编队队形, 例如锥形编队飞行, 其中直线上相邻两架无人机间距相等.设计纯方位无源定位情形下, 无人机的位置调整方案.
- 问题分析
2.1 问题一思路分析
对本文提出的有关无人机定位问题，我们逐一做如下分析：
问题一主要围绕十架无人机形成圆形编队且保持同一高度飞行时, 通过若干无人机发射的信号实现纯方位无源定位的问题, 那么此时只需要考虑平面上的圆周问题就可以了.根据问题一的假设, 剩下的九架飞机尽量均匀分布在圆周上, 对于位置准确的无人机, 其位置仅与无人机的编号有关, 而对于位置略有偏差的无人机, 他们距离圆心无人机的距离以及角度都是暂时不知道的. 我们需要对下述三种情况进行分析：
- 当位于圆心无人机（FY00）和编队中已知编号且位置无偏差的两架无人机发射信号, 建立被动接收信号无人机的定位模型. 对该问题, 我们有两种想法进行求解, 一种是建立极坐标, 根据已知的方向信息, 按照被动无人机是否在已知无人机位置中间的情况划分, 利用平面上三角形的正弦定理, 联立方程, 得到最终的结果；另一种是利用三角测量定位法, 通过求解一个最小二乘问题求得无人机的位置.
- 与上一问相比, 该问题中我们无法得知除FY00和FY01外其余发射信号的无人机的编号, 无法直接利用三角测量定位法进行求解. 因此使用交叉定位方法进行求解, 我们逐一增加位置略有偏移的发射无人机的数目, 直到可以确定无人机的位置.
- 第三小问需要对初始时刻位置存在偏差的无人机的位置进行调整.由前两问已知实现无人机的有效定位, 至少需要圆周上两架无人机发送信号.由于发送信号的无人机位置存在偏差, 因此我们可以利用贪婪策略使得无人机每次进行位置调整的误差最小.
2.2 问题二的思路分析
问题二是一个动态规划问题.与问题一不同的是, 问题二的无人机一定在同一高度飞行, 因此, 我们需要利用动态规划模型, 寻找使得无人机在调整过程中偏差尽可能小的方案.
三、模型假设
针对本文提出的问题，我们做了如下模型假设：
假设1：题目中的无人机略有偏差时, 还大体在理想位置, 不存在偏离超
过XX范围的无人机；
假设2：假设每架无人机标号都是固定的, 且明确知道哪些无人机发射信号；
四、符号说明
本文常用符号见下表, 其它符号见文中说明
| 符号 | 符号意义 |
| z | 复数域内的自变量 |
| w | 复数域内的自变量 |
| f(z) | C→C |
的复变函数五、建模与求解
5.1 问题一的建模与求解
5.1.1 使用极坐标求解具体位置
, α=2π/9
.以无人机FY00为极点, 以FY00为端点且经过FY01的射线为极轴建立极坐标系.不失一般性, 假设在圆周上的其中一架发射信号无人机为FY01, 转化为极坐标后, 其对应的极坐标为 (R,0
). 由于发射信号的无人机都是位置准确的, 所以另一架发射信号无人机的位置是根据编号固定的, 编号为FY0K, 由于理想状态下, 所有无人机均匀分布在圆周上, 则其对应的坐标为 (R, (k-1)α)
, 其中K≠0,1
接着, 假设接受信号的无人机ρ
的极坐标位置为 (x, θ)
, 由于剩下无人机的位置略有偏差, 所以两个参数都需要进行确定. 接着, 我们去假设它与三架发射信号的无人机的夹角. 假设ρ
与FY00、FY01之间的夹角为α1
, ρ
与FY00、FY0K之间的夹角为α2
, ρ
与FY01、FY0K之间的夹角为α3
.接下来需要通过已知信息来确定出相应接收信号无人机的极坐标(x, θ)
.
我们将略有偏差的无人机与确定的无人机位置相连, 利用正弦定理, 通过联立方程组来解得极坐标 (x, θ)
. 下面由于牵扯到角度, 还需要对K的不同值进行分类讨论：
情况i）当K=2时, 两个外围确定的无人机之间没有其他无人机：分布情况可视化如下图5.1所示：
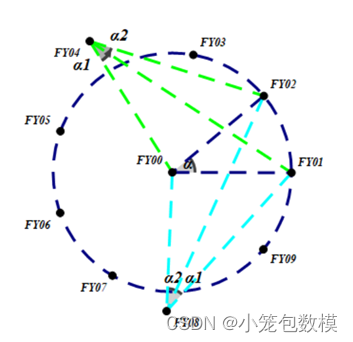
图5.1 两个外围确定的无人机之间没有其他无人机分布图
由上图5.1可知：若α1≤α2
(绿色所示位置), 我们考察FY00、FY01、FY0K构成的三角形与FY00、FY02、FY0K构成的三角形, 根据正弦定理可得：
sin(α1)R=sin(π-θ-α1)xsin(α2)R=sin(π-(θ-(k-1)α+α2))x
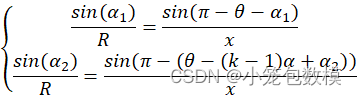
sin(α1)R=sin(π-θ-α1)xsin(α2)R=sin(π-(θ-(k-1)α+α2))x
, （5-1）
由式（5-1）解得：
θ=arctan(sin(α1)*sin(α2)-sin(α1)*sin(α2-(k-1)α)sin(α1)*cos(α2-(k-1)α)-sin(α2)*cos(α1))x=sin(θ+α1)*Rsin(α1)
； （5-2）
根据图5.1可知：若α1>α2
(蓝色所示位置), 我们考察FY00、FY01、FY0K构成的三角形与FY00、FY02、FY0K构成的三角形, 根据正弦定理可得：
sin(α1)R=sin(π-θ-α1)xsin(α2)R=sin(π-((2π-θ)+(k-1)α+α2))x
, （5-3）
由式（5-3）解得：
θ=arctan(sin(V)*sin(α2)+sin(α1)*sin(α2+(k-1)α)sin(α1)*cos(α2+(k-1)α)-sin(α2)*cos(α1))x=sin(θ+α1)*Rsin(α1)
； （5-4）
情况ii）当K=3,4,5时, 我们需要根据α3
的大小判断有偏差的无人机是否夹在两个确定位置的无人机中间：分布情况可视化分析如图5.2所示
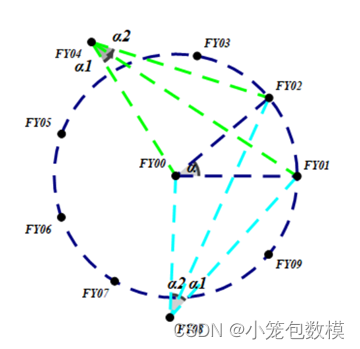
图5.2 情况ii无人机分布情况可视化分析
图5.2中：若α3<π2
且α2=α3+α1时，
此时无人机并不处于两架飞机之间, 和上一种情况一致, 列出方程为:
sin(α1)R=sin(π-θ-α1)xsin(α2)R=sin(π-(θ-(k-1)α+α2))x
（5-5）
解得：
θ=arctan(sin(α1)*sin(α2)-sin(α1)*sin(α2-(k-1)α)sin(α1)*cos(α2-(k-1)α)-sin(α2)*cos(α1))x=sin(θ+α1)*Rsin(α1)
； （5-6）
图5.2中：若α3<π2
且α3=α2+α1时，
此时无人机并不处于两架飞机之间, 和上一种情况一致, 列出方程为:
sin(α1)R=sin(π-θ-α1)xsin(α2)R=sin(π-((k-1)α-θ+α2))x
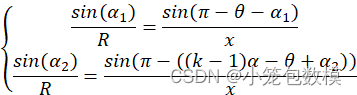
（待更新... ...）
