方差分析这部分内容还不是很理解，在这里先做一个笔记，以后有时间再回过头来改一改。
用到的数据集$\to$Iris

什么是假设检验？
假设检验就是利用样本数据对某个事先做出的统计假设，再按照某种方法去检验，最后判断此假设是否正确。

怎么去假设检验？
假设检验的目的是为了推断总体。首先对总体的未知参数或分布做出某种假设$H_0$，然后在$H_0$成立的条件下，若通过抽样分析发现“小概率事件”竟然在一次实验中发生了（在这里我们是不希望小概率事件发生的），则表明$H_0$很可能不成立，从而拒绝$H_0$；相反，若这个“小概率事件”没有发生，则没有理由拒绝$H_0$，从而接收$H_0$。

⭐️ 检验的显著性水平（$\alpha$）：要求“小概率事件”发生的概率小于等于某一给定的临界概率。通常$\alpha$的取值为较小的数0.05、0.01、0.001。
⭐️ P值：假定原假设$H_0$为真时，“拒绝原假设$H_0$”这件事犯错的可能性。当P值$<\alpha$时，表示“拒绝原假设$H_0$”这件事犯错误的可能性很小，即可以认为原假设$H_0$是错误的，从而拒绝$H_0$；否则，应接收原假设$H_0$。

🌕 数据分布检验

数据分布的假设检验是重要的非参数检验，它不是针对具体的参数，而是根据样本值来判断总体是否服从某种指定的分布。

🌗 数据准备

# 导入相关的库
import numpy as np
from matplotlib import pyplot as plt
from scipy import stats
# 中文显示问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)

np.random.seed(123)			# 设置随机数种子
X1 = stats.norm.rvs(loc = 0,scale = 1,size = 500)		# X1为服从均值为0方差为1的标准正态分布数据
X2 = stats.norm.rvs(loc = 0,scale = 5,size = 500)		# X2为服从均值为0方差为5的正态分布数据
X3 = stats.f.rvs(15,30,size = 500)						# X3为服从均值为15方差为30的非正态分布数据
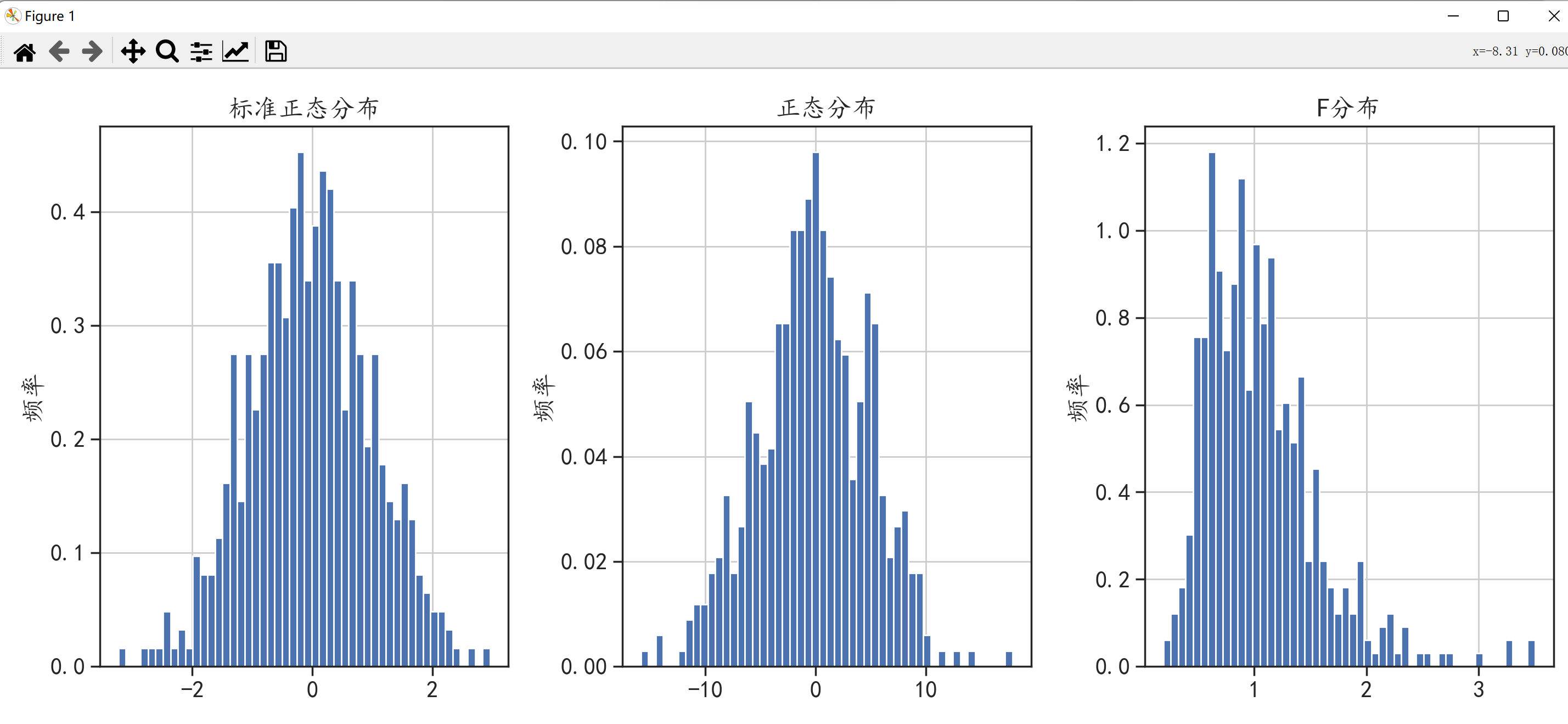
plt.figure(figsize = (15,6))
plt.subplot(1,3,1)							# 将画布分为一行三列（三部分），现在对从左至右从上至下第一个子图操作
plt.hist(X1,bins = 50,density = True)		# X1的频率直方图（density=True表示频率，False表示频数。默认为频数）
plt.grid()
plt.ylabel("频率")
plt.title("标准正态分布")
plt.subplot(1,3,2)							# 对第二个子图操作
plt.hist(X2,bins = 50,density = True)
plt.grid()
plt.ylabel("频率")
plt.title("正态分布")
plt.subplot(1,3,3)							# 对第三个子图操作
plt.hist(X3,bins = 50,density = True)
plt.grid()
plt.ylabel("频率")
plt.title("F分布")
plt.tight_layout()							# 防止子图间轴域的标签叠在一起
plt.show()

🌗 利用Q-Q图检验数据是否符合正态分布

什么是Q-Q图？
Q-Q中的两个Q都是quantile（分位数）的缩写，也就是说Q-Q是横纵坐标都关于分位数的一个图。那么说到这里，

什么又是分位数？
分位数也称分位点，是指将一个随机变量的概率分布范围分为几个等份的点，常用的有中位数（二分位数）、四分位数、百分位数等。

Q-Q图的作用即标题，是用来检验数据是否符合正态分布的，它就是先将两列数据的分位点画成散点图，然后比较两列数据的分位点是否分布在y=x的直线上，若是，则接收数据来自正态总体的假设，否则就拒绝原假设。

在这里我们可以使用statsmodels.api模块中的qqplot()函数来绘制Q-Q图。

import numpy as np
from matplotlib import pyplot as plt
from scipy import stats
import statsmodels.api as sm		# 导入Q-Q图要用的模块

import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font="Kaiti",style="ticks",font_scale=1.4)

np.random.seed(123)
X1 = stats.norm.rvs(loc = 0,scale = 1,size = 500)
X2 = stats.norm.rvs(loc = 0,scale = 5,size = 500)
X3 = stats.f.rvs(15,30,size = 500)

fig = plt.figure(figsize = (15,5))
ax = fig.add_subplot(1,3,1)			# add_subplt与subplot是一个东西，没有太大的区别，只是调用的方式不一样
sm.qqplot(X1,line = "45",ax = ax)	# 绘制X1的Q-Q图，line=45是绘制45°斜直线
plt.grid()
plt.title("X1正态检验Q-Q图")
ax = fig.add_subplot(1,3,2)
sm.qqplot(X2,loc = 0,scale = 5,line = "45",ax = ax)	# 绘制X2的Q-Q图
plt.grid()
plt.title("X2正态检验Q-Q图")
ax = fig.add_subplot(1,3,3)
sm.qqplot(X3,line = "45",ax = ax)	# 绘制X3的Q-Q图
plt.grid()
plt.title("X3正态检验Q-Q图")
fig.tight_layout()
plt.show()

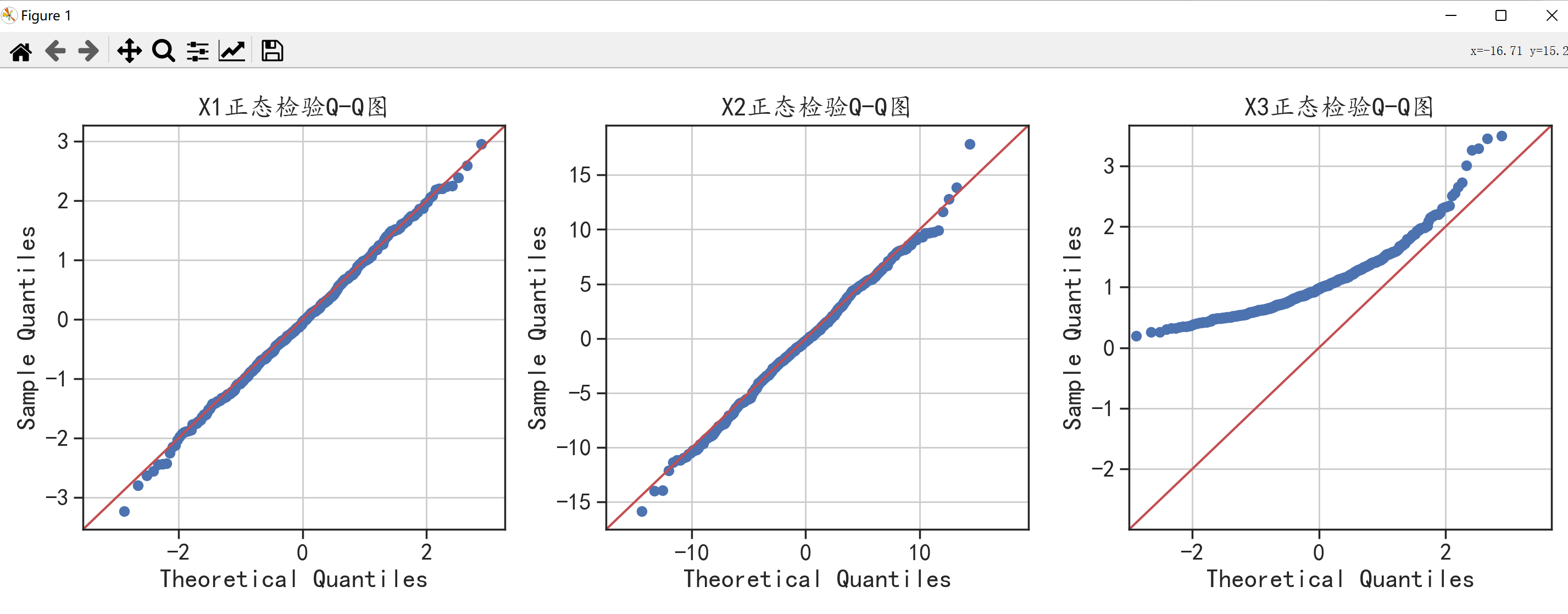
可以发现，前两个图的散点图都能很好地拟合参考线，表示X1和X2是正态分布，而第三个图的散点图没有在参考线上，表示X3不是正态分布。

🌗 利用K-S拟合优度检验来检验数据是否符合正态分布

K-S检验可以使用stats.kstest()函数完成，默认情况下会验证数据是否符合标准正态分布，同时可以指定cdf参数所要验证的分布类型，还可以利用args参数指定符合参数的特定分布。

# 这里还是用随机数种子“123”
print(stats.kstest(X1,cdf = "norm"))				# X1的标准正态分布检验
print(stats.kstest(X2,cdf = "norm"))				# X2的标准正态分布检验
print(stats.kstest(X2,cdf = "norm",args = (0,5)))	# X2的正态分布检验
print(stats.kstest(X3,cdf = "norm"))				# X3的标准正态分布检验
print(stats.kstest(X3,cdf = "f",args = (15,30)))	# X3的非正态分布检验

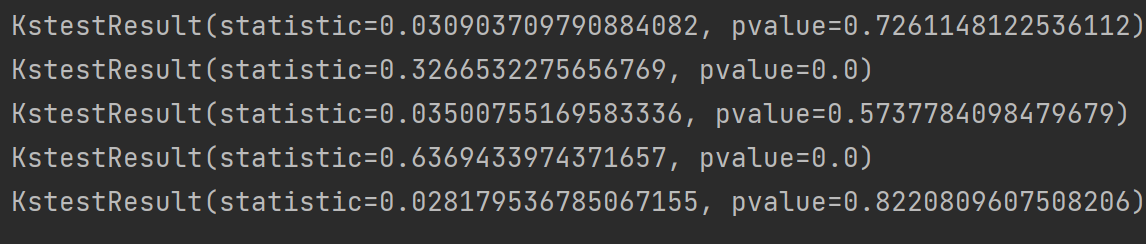
从结果中我们可以看到，在对X1的标准正态分布检验中，P值大于0.05（在前面回顾一下P值的概念），就说明了“拒绝原假设”这件事犯错误的可能性比较大了，也就是说拒绝原假设会犯错误，那么我们就应该接收原假设，即X1是服从标准正态分布的。（0.05是检验的显著性水平，是人为取值的）

又如在X2的标准正态分布检验中，它的P值为0，但本质上是不为0的，因为这个P值很小很小（5.2306133517677304$\times 10^{-48}$)，所以程序就直接省略了。那就是这个P值它是小于0.05，说明“拒绝原假设”这件事犯错误的可能性比较小，那么我们就应该拒绝原假设，即X2不服从标准正态分布。

后面几个结果也是同样的分析。

K-S检验还可以用stats.ks_2samp()函数检验两个随机变量的分布是否相同

print(stats.ks_2samp(X1,X2))
print(stats.ks_2samp(X2,X3))
print(stats.ks_2samp(X3,X1))

同样，也是根据P值来判断它们是否具有相同的分布。

🌕 t检验

t检验分为单样本t检验和两独立样本t检验。

⭐️ 单样本t检验：检验来自正态分布的样本的期望值（均值）是否为某一实数。
⭐️ 两独立样本t检验：判断两个来自正态分布（方差相同）的独立样本的期望值之差是否为某一实数。

两种检验的原假设都是差等于指定值。

🌗 单样本t检验

import numpy as np
from scipy import stats

np.random.seed(123)
X1 = stats.norm.rvs(loc = 0,scale = 1,size = 500)	# 标准正态分布随机数X1
X2 = stats.norm.rvs(loc = 0,scale = 5,size = 500)	# 正态分布随机数X2
X3 = stats.norm.rvs(loc = 5,scale = 5,size = 500)	# 正态分布随机数X3
print(stats.ttest_1samp(X1,0))		# 检验X1的均值是否为0
print(stats.ttest_1samp(X2,5))		# 检验X2的均值是否为5
print(stats.ttest_1samp(X3,5))		# 检验X3的均值是否为5

从第一组的检验结果可以发现，它的P值大于0.05，也就是说“拒绝原假设”这件事犯错误的可能性比较大，所以应该接受原假设，即X1的均值为0，剩下两组的判断也是如此。

🌗 两独立样本的检验

print(stats.ttest_ind(X1,X2))	# 检验X1和X2的均值之差是否等于0
print(stats.ttest_ind(X2,X3))	# 检验X2和X3的均值是否相等
print(stats.ttest_ind(X3,X1))	# 检验X3和X1的均值是否相等

从结果分析，我们可以知道X1和X2的均值相等，X2和X3的均值不相等，X3和X1的均值也不相等。

🌕 方差分析

方差分析是分析实验数据的一种方法。

对于抽样测得的实验数据，由于观测条件不同或随机因素的干扰造成的差异使得实验结果不同，将前者造成的差异称为系统差异和偶然差异。

方差分析的目的：从实验数据中分析出各个因素及它们之间产生的影响，确定各个因素作用的大小，进而把两种差异区分开来，以确定在实验中有没有系统的因素在起作用。

方差分析根据因素数量，可分为单因素方差分析、双因素方差分析等。

🌗 单因素方差分析

使用sm.stats.anova_lm()函数完成方差分析（l是小写L），使用pairwise_tukeyhsd()函数对数据方差分析结果进行多重检验。

import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf

a = pd.read_csv("D:/Pycharm/机器学习数据/program/data/chap2/Iris.csv")	# 读取数据
model = smf.ols("SepalLengthCm~Species",data = a).fit() 
b = sm.stats.anova_lm(model,typ = 2)	# 方差分析
print(b)

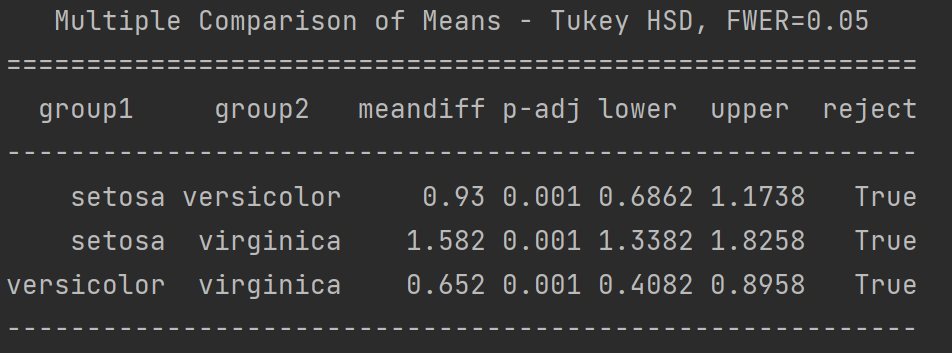
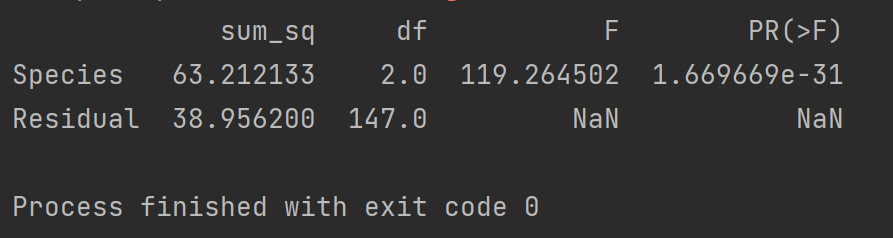最后一个PR是P值，远小于0.05，则应该拒绝原假设，说明不用类别的SepalLengthCm特征均值不完全相同。那么我们可以使用多重比较对比哪些类别之间的均值不同。

import pandas as pd
from statsmodels.stats.multicomp import pairwise_tukeyhsd

a = pd.read_csv("D:/Pycharm/机器学习数据/program/data/chap2/Iris.csv")
b = pairwise_tukeyhsd(endog = a.SepalLengthCm,groups = a.Species,alpha = 0.05)
print(b)

针对于获得的多重比较的结果，可以使用plot_simultaneous()函数可视化出多重比较的图像。

b.plot_simultaneous()
plt.grid()
plt.show()

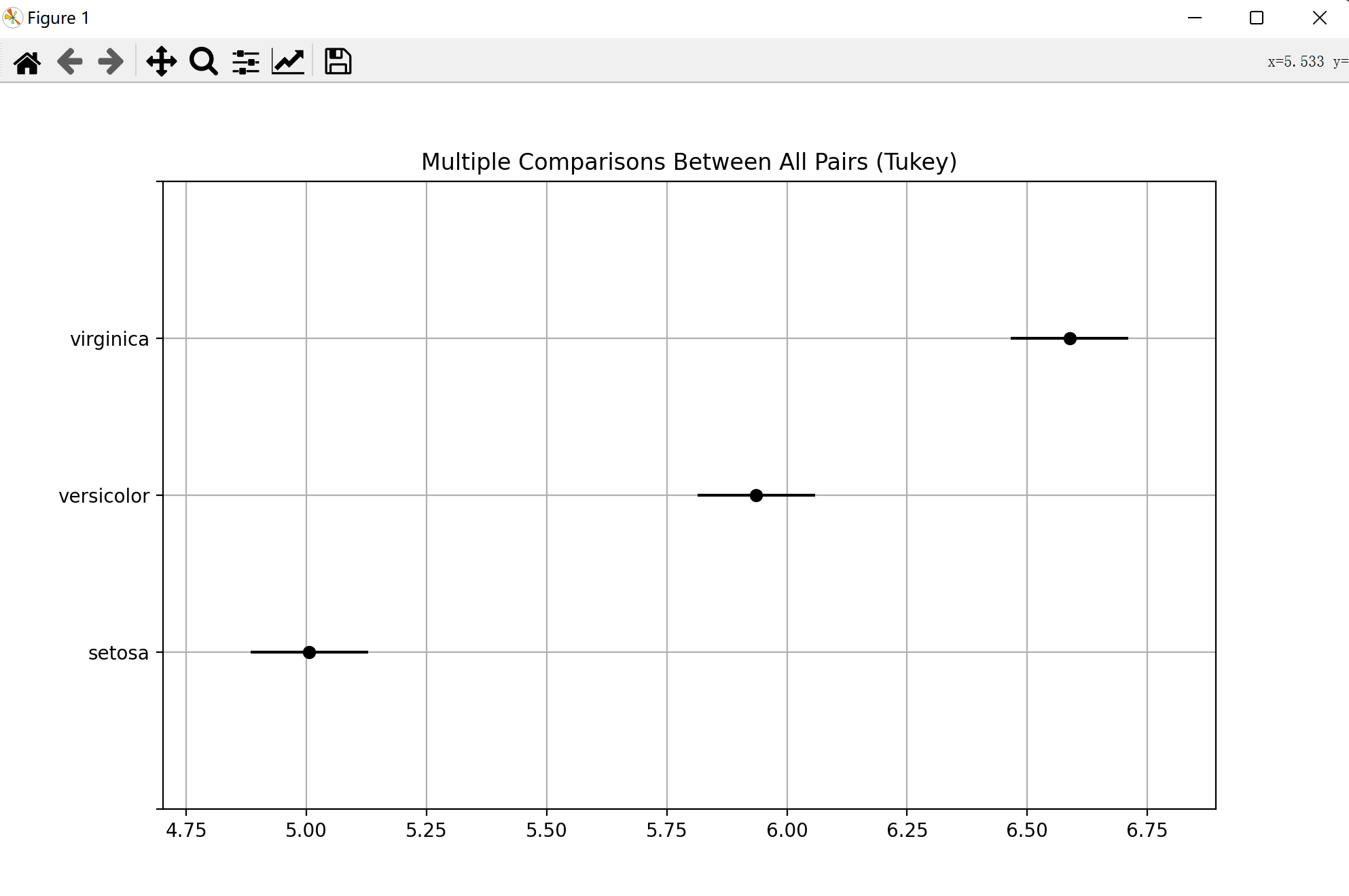
可以直观的看出，三个类别的均值都不相同或，且setosa的均值最小，virginica的均值最大。

🌗 双因素方差分析

双因素方差分析分为两种情况，分别是不考虑交互作用和考虑交互作用的情况。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf

a = pd.read_csv("D:/Pycharm/机器学习数据/program/data/chap2/Iris.csv")

np.random.seed(123)
a["Group"] = np.random.choice(["A","B"],size = 150)		# 生成新的分类因素Group
model = smf.ols("SepalLengthCm~Species * Group",data = a).fit()
b = sm.stats.anova_lm(model,typ = 2)
print(b)

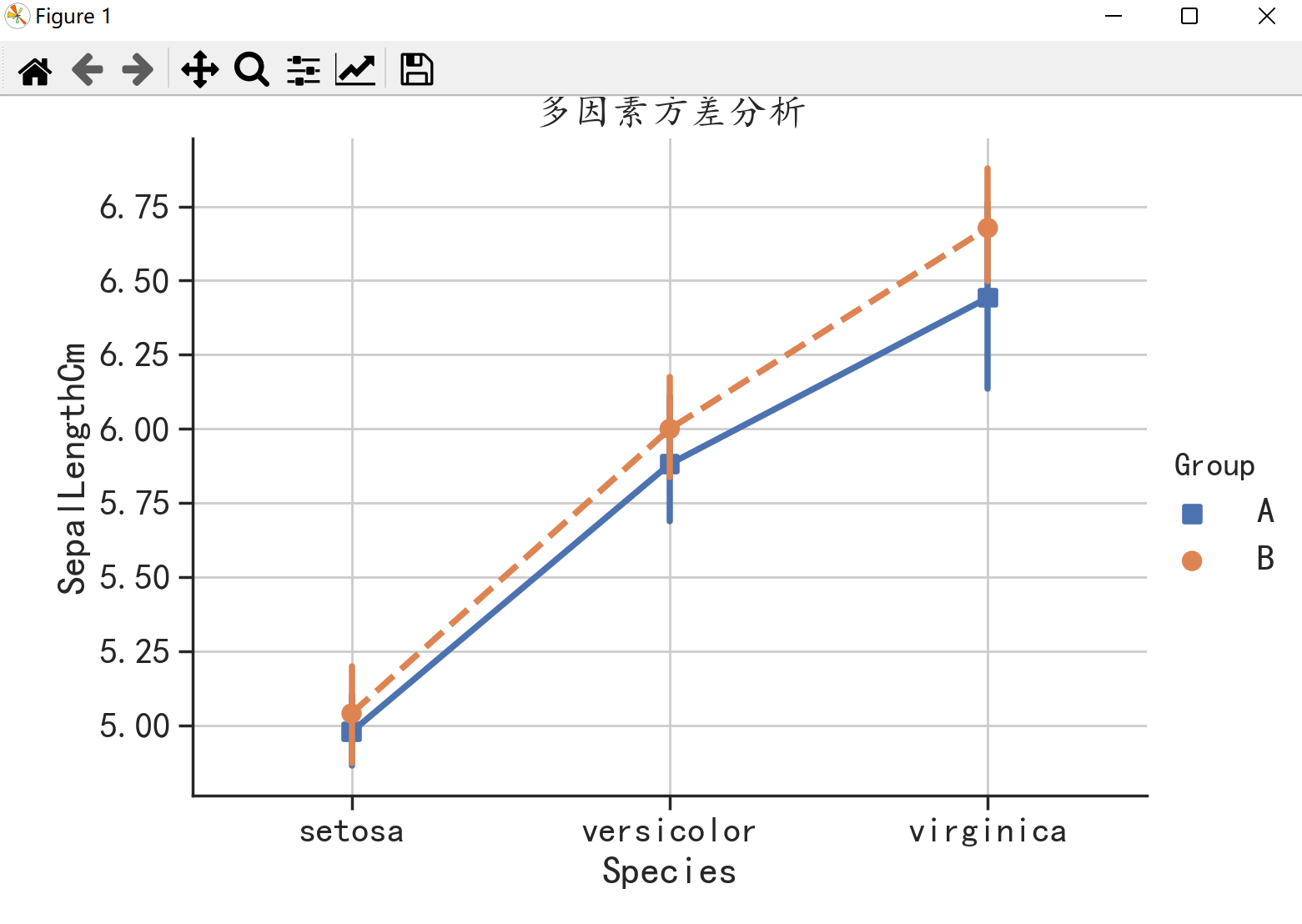
从结果可以看出，Species因素下差异是显著的。Group因素和Species:Group（Species和Group的交互作用）因素下差异是不显著的。

针对双因素影响的数据，可以使用sns.catplot()函数将其可视化。

import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from matplotlib import pyplot as plt
import seaborn as sns

import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
sns.set(font="Kaiti",style="ticks",font_scale=1.4)

a = pd.read_csv("D:/Pycharm/机器学习数据/program/data/chap2/Iris.csv")
np.random.seed(123)
a["Group"] = np.random.choice(["A","B"],size = 150)
model = smf.ols("SepalLengthCm~Species * Group",data = a).fit()
b = sm.stats.anova_lm(model,typ = 2)
sns.catplot(x = "Species",y = "SepalLengthCm",hue = "Group",markers = ["s","o"],linestyles = ["-","--"],data = a,kind = "point",aspect = 1.4)
plt.grid()
plt.title("多因素方差分析")
plt.show()