题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
解析
这道题目,求的是子序列,要求的是不一定连续,但应该相对有序;
还是用动归五部曲来分析下:
1.确定dp数组及其含义
需要一个二维数组dp[i][j],表示长度为[0,i-1]的字符串text1和长度为[0,j-1]的字符串text2,最长公共子序列为dp[i][j],至于为什么要算i-1,和上一道题一样,只是为了写代码的时候好处理
2.确定递推公式
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
3.初始化DP数组
初始化为0
func longestCommonSubsequence(text1 string, text2 string) int {
m := len(text1)
n := len(text2)
dp := make([][]int, m+1)
for i := range dp {
dp[i] = make([]int, n+1)
}
// 上面这里已经初始化为0了
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if text1[i-1] == text2[j-1] {
dp[i][j] = dp[i-1][j-1] + 1
} else {
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
}
}
}
return dp[m][n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
同时题目1035 不相交的钱,其实和这道题是一模一样的
题目
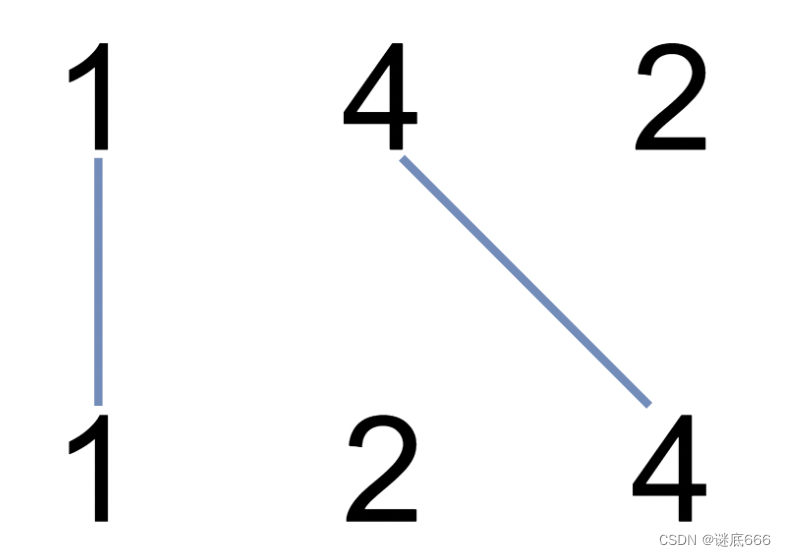
我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
以这种方法绘制线条,并返回我们可以绘制的最大连线数。
本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!