目录
- 一、B+树索引
- 1.1 在没有索引时进行查找记录
- 1.2 索引方案
- 1.3 InnoDB中的索引方案
- 二、聚簇索引
- 三、二级索引
- 四、联合索引
- 五、InnoDB中B+树索引的注意事项
- 5.1 根页面的位置不会改变
- 5.2 内节点中目录项记录的唯一性
- 5.3 一个页面至少容纳两条记录
一、B+树索引
数据库中的用来存储数据的数据页之间组成一个双向链表,并且每个数据页中的记录按照主键值从小到大的顺序组成一个单向链表,同时在每个页中都有一个页目录,在某页中查找记录时,通过二分法定位到对应的槽,遍历该槽对应分组中的记录便可找到目的记录。
1.1 在没有索引时进行查找记录
很多时候,一个表中的记录需要存储到多个数据页中,因此定位到某条记录分为两步:
- 定位到记录所在的页
- 在所在页中查找相应的记录
由于没有创建索引,所以需要从第一个数据页沿着双向链表查找,在每一页中通过二分法的方式定位到槽,然后再对应的分组中查找记录,由于需要遍历所有的页,这种方式是十分耗时。
1.2 索引方案
在没有索引是进行查找需要遍历所有页是因为各个页中的记录排列是没有规律的,而当建立索引后,各个页中的记录会根据索引列从小到大进行排序,同时下一页中的记录大于上一页中的记录。记录有序还不足够,还要给所有的页建立一个目录
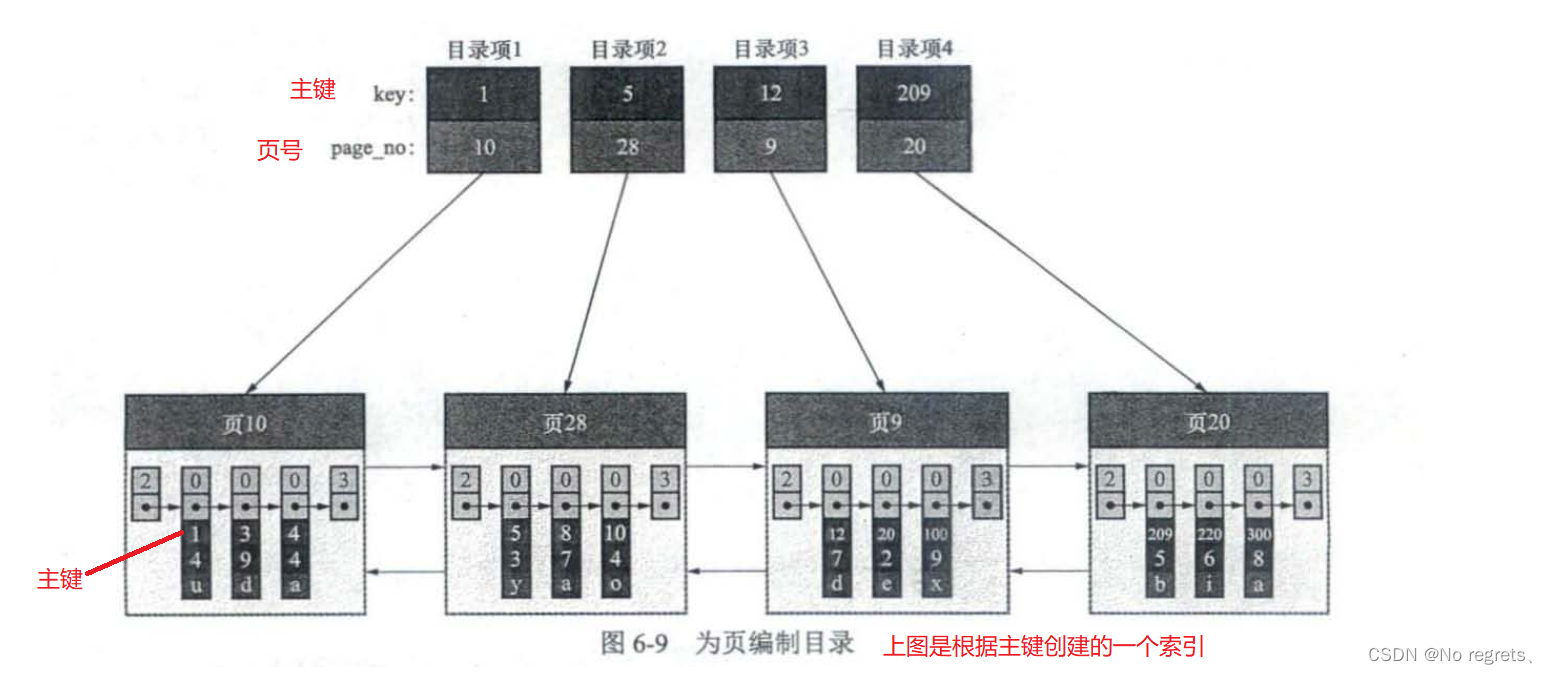
通过上述索引查找某条记录也是分为两步:
- 根据二分法在目录项中找出记录所在的页号
- 在所在页中定位到要查找的记录
1.3 InnoDB中的索引方案
上述根据二分法在目录项中查找记录是建立在所有的目录项都存储到一个页面中的基础上,但在实际的InnoDB中,一个页大小为16KB,当表中记录非常多的时候,就无法将所有的目录项装在同一个页中。
InnoDB给出的是这样的解决方案,发现目录项和用户记录很相似,只不过目录项中的两个列分别是主键和页号,因此他们决定将目录项记录也存储到数据页中,

当表中的数据非常多时,就会产生很多存储目录项记录的页,为了能够根据主键快速定位到一个存储目录项记录的页,需要为存储目录项记录的页创建一个跟高级的目录,具体示意图如下
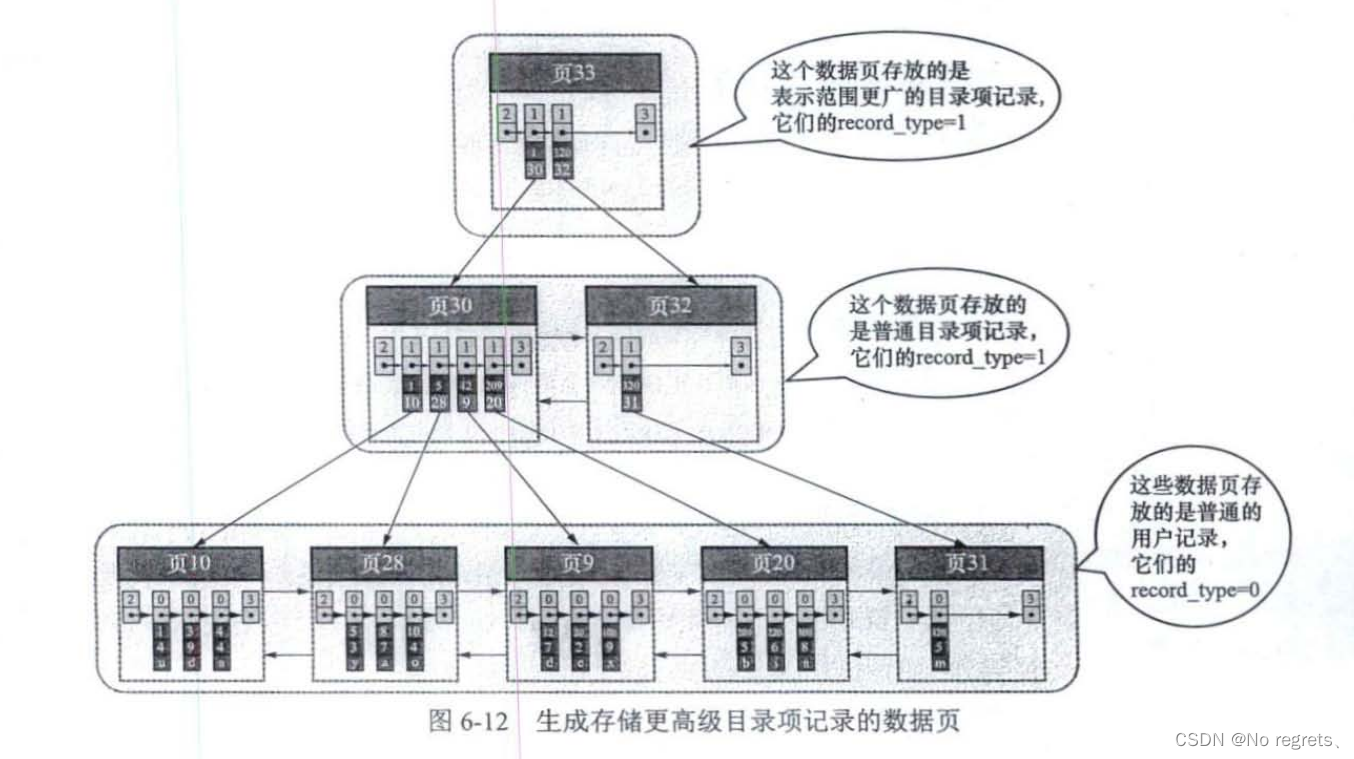
而上面这种组织数据的格式其实就是B+树,无论是存放用户记录的数据页还是用来存储目录项记录的数据页,都存放到B+树中,真正的用户记录只出现在叶子节点中,非叶子节点中存储的是目录项记录。
【为什么B+树的层数一般不会超过4层呢?】
我们首先假设一个页能存储100条用户记录,一个页能存储1000条目录项记录,当B+树有4层时,那么最多能存放的记录数时100010001000*100=1000亿条记录
因此在通过主键值去查找某条记录时,最多只需进行4个页面内查找(3个目录项记录的页和1个存储用户记录的页)。
二、聚簇索引
聚簇索引是指记录之间根据主键值进行排序,包括3方面含义:
(1)页内记录按照主键的大小顺序排成一个单向链表
(2)存放用户记录的页之间根据页中用户记录的主键大小顺序排成一个双向链表
(3)存放目录记录的页之间也会根据记录的主键顺序排成一个双向链表
InnoDB存储引擎会自动为我们创建聚簇索引
三、二级索引
聚簇索引只能在搜索条件是主键值时才能发挥作用,如果搜索条件中包含的并不是主键列,二级索引就是解决这个问题的,二级索引的B+树如下图:
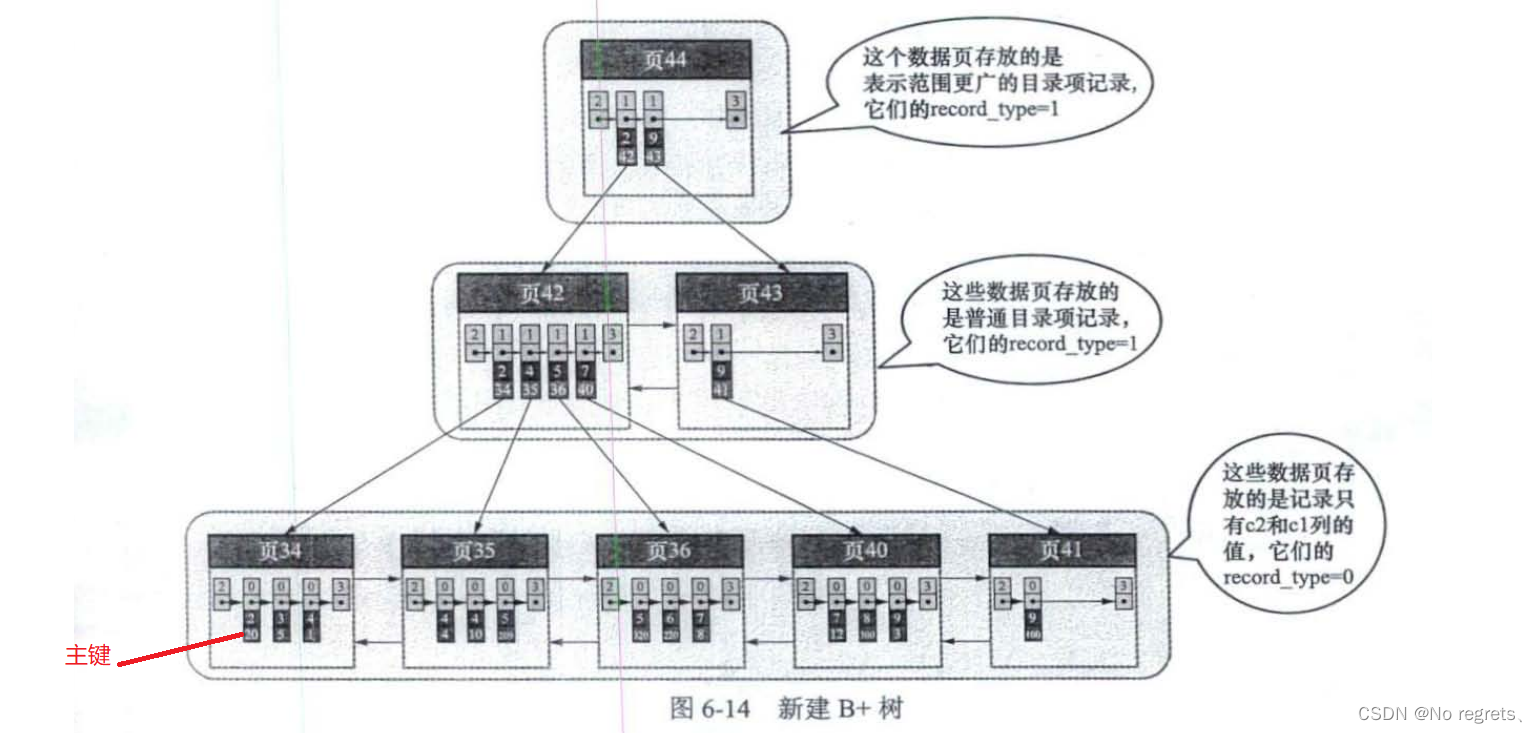
二级索引与聚簇索引的不同之处:
- 二级索引中,记录根据普通列的大小对页中记录和页之间进行排序
- B+树的叶子节点只包含作为排序依据的列和主键列,并不是完证的用户记录
- 目录项记录中不再是主键+页号,而变为作为排序依据的列+页号
通过二级索引查找一个记录的过程如下,假设作为排序依据的列是c1列,搜索条件是c1=10
- 首先确定符合c1=10的目录项记录所在的页
- 通过符合c1=10的目录项所在的页确定c1=10的用户记录所在的页
- 在符合c1=10的用户记录中查找这条记录
- 由于叶子节点主存储了c1列和主键列,因此还要通过该记录的主键值到聚簇索引中找出完整的用户记录(这个过程也叫做回表)
【为什么二级索引的叶子节点不存储完整的用户记录呢?】
原因很简单,太浪费空间了
四、联合索引
同时以多个列的大小作为排序规则,例如可以让B+树按照c1和c2列的大小进行排序,具体含义就是,先根据c1进行排序,在c1相同的情况下根据c2进行排序
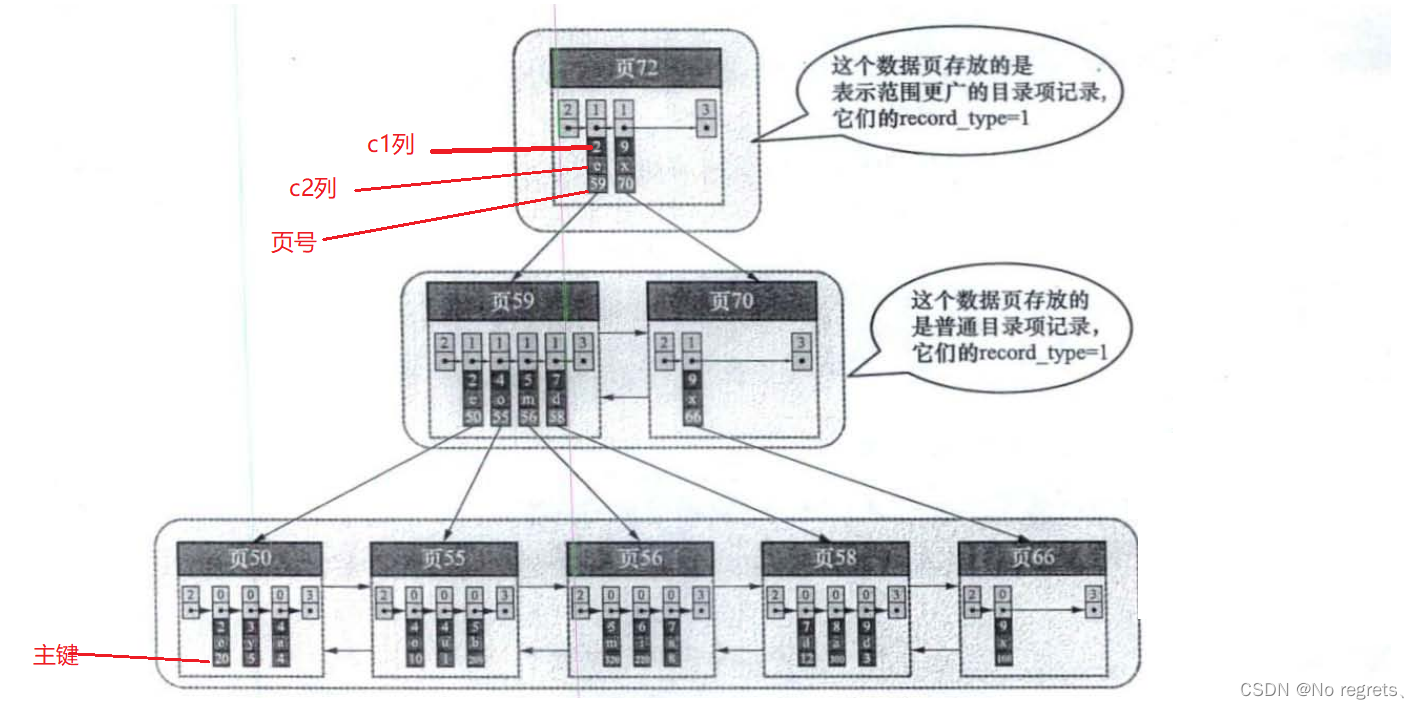
五、InnoDB中B+树索引的注意事项
5.1 根页面的位置不会改变
实际生成B+树的过程如下:
- 为某个表创建一个B+树索引的时候,都会为这个索引创建一个根节点的页面,在没有向表中插入数据的时候,根页面中也没有数据
- 随着向表中插入数据,会先把用户记录存储到根页面中
- 当根页面中存储不下用户记录时,再向表中插入页面时,会进行页分裂的操作,也就是产生两个新的页,将根页面中的用户记录复制到这两个新页中,根节点便升级为存储目录项记录的页
由于索引的根页面的页号是永远不会变的,因此会将这个页号存储到某个地方,后续需要用到这个索引时,就会取出根页面,对该索引进行访问
5.2 内节点中目录项记录的唯一性
在前面了解到,对于二级索引来说,在目录项记录存储的是索引列+页号,但这样存储有一个问题就是,对于二级索引的索引列的值可能不是唯一的,这就可能产生一个问题,两个目录项记录的索引列值相同但页号不同,碰巧将要新插入的记录的索引列值和这两个值也相同,那么这个新插入的记录究竟要放到哪页中呢?
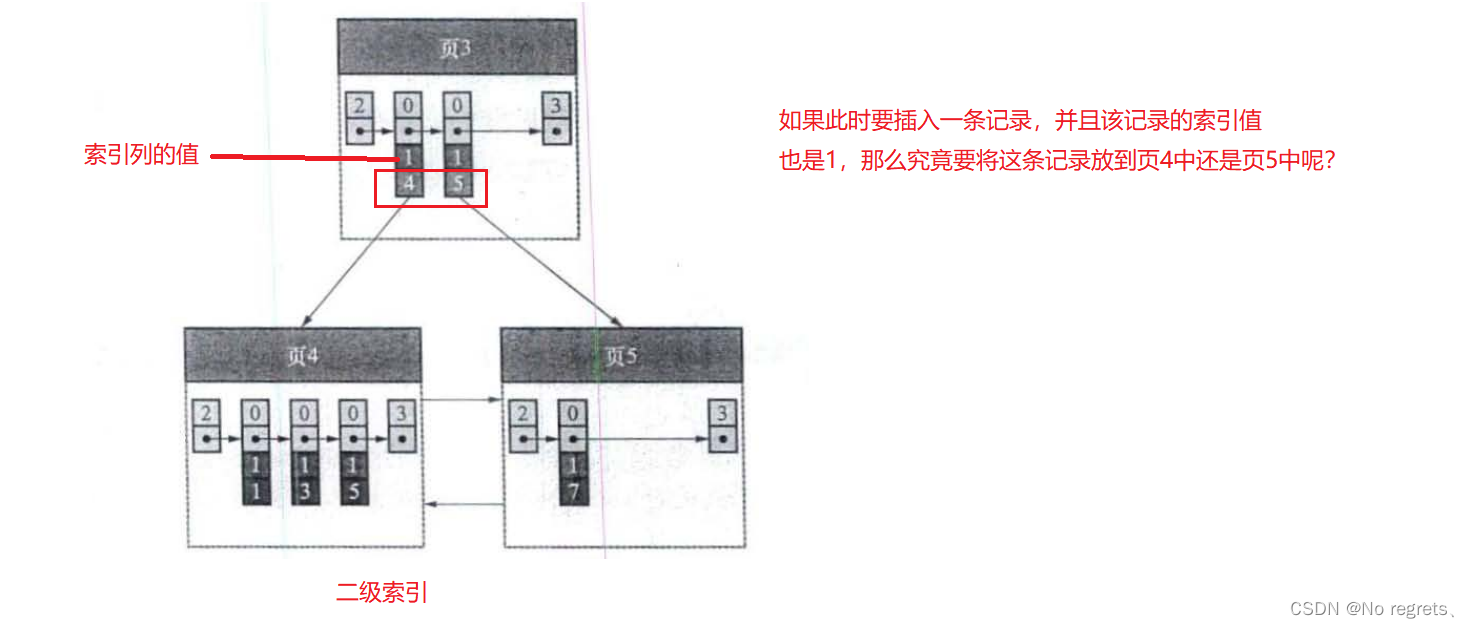
为了解决这个问题,InnoDB给出的解决方案是,在二级索引的目录项记录中,存储索引列值+主键+页号,这样就能保证除页号以外的其他目录项记录字段是唯一的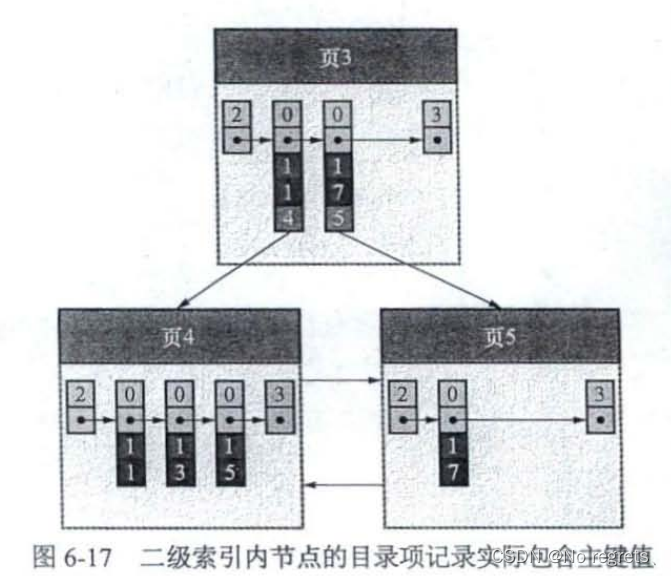
5.3 一个页面至少容纳两条记录
为了避免B+树的层级过高,InnoDB规定所有的数据页至少可以容纳两条记录
内容参考《MySQL是怎样运行的》