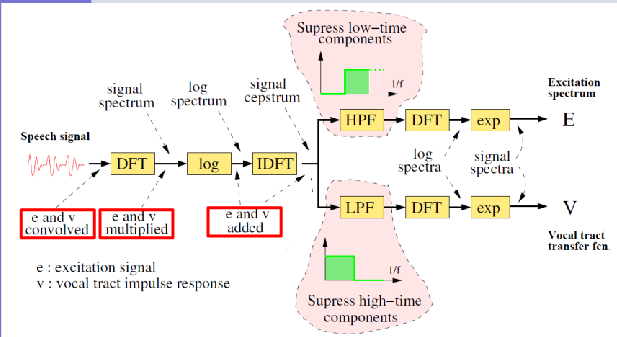
源过滤器分离
倒谱分析是另一种将声道滤波器响应与激励分开的方法(如线性预测)
它基于以下观察:语音信号的频谱是激励频谱和声道频率响应的乘积
可以使用log将乘法转换为加法,因此,“对数频谱”可以看作是对数激励频谱和对数声道频率响应的总和
log(spectrum) = log(excitation spectrum) + log( vocal tract frequency response)
所以,如果对数频谱被视为波形,那么它就可以被过滤掉!
这种方法称为同态滤波 homomorphic filtering
可以在时域或频域中对序列进行滤波,对数的谱图叫倒谱,(经常使用的实数)倒谱正式定义为“信号对数幅度谱的傅立叶逆变换”。
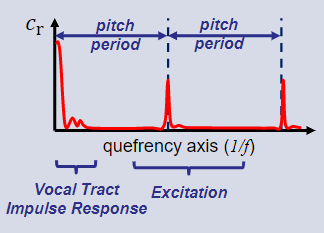
倒谱 Cr[m] 在quefrency域中计算
Quefrency 以时间单位 (1/f) 衡量
在反频域中进行过滤称为提升liftering
倒谱分析的应用
音高估计Pitch estimation
——基于在高反频分量中找到峰值倒谱值
平滑频谱估计 Smoothed spectrum estimation
——基于对(零填充)低反频分量进行 DFT
——提供了 LP 频谱的替代方案
声码 Vocoding
– 基于估计基频并将语音作为低逆频倒谱帧序列传输
Automatic speech recognition自动语音识别
– 基于使用低逆频倒谱分量作为(平滑的)频谱的表示
– “梅尔频率倒谱系数”(MFCC) Mel Frequency Cepstrum Coefficients
梅尔频率倒谱系数
MFCC 是对完整倒谱系数的实用近似…
– 频率标度是非线性的
– 使用滤波器组计算频谱
– 使用“离散余弦变换”(DCT) 估计倒谱系数
MFCC 不是实现一组(计算量大的)数字滤波器,而是通常使用 DFT 计算,其输出分为 20-40 个频带
MFCCs 有几个吸引人的特性…
- 它们解除了频谱中信息的相关性
- 只需要几个参数 (10-15) 来表示每个帧
好的声学特征有的特性
• 所有与信号解释相关的信息都必须包含在特征中
– 解释所需的足够信息
– 没有太多(不相关)信息
• 高效计算
• 好的特征概括得很好 –
一个人的“A”应该以相同的方式表示作为来自其他人的“A”
• 特征向量 X 代表语音
• 关于“子词”的信息应该很好地呈现
梅尔音阶 The Mel Scale
“梅尔音阶”是一种非线性频率音阶,反映了听觉音调感知的某些方面
该名称源自“旋律”一词
该音阶通常被认为在高达 1kHz 时近似线性,此后为对数