常见递归模式

news2024/11/15 7:56:45

常见递归模式

递归模式
遍历二叉树模式
回溯模式
子问题分解模式

递归模式

常见递归模式：

遍历二叉树模式
回溯模式
子问题分解模式

遍历二叉树模式

只要涉及递归的问题，都是树的问题，或者说树的遍历。

void traverse(TreeNode root) { // 遍历二叉树
    if (root == null) return;  // 递归结束条件
    print(root.val)            // 前序位置，在进入左节点前，输出当前节点
    traverse(root.left);       // 进入左子树
    print(root.val)            // 在中序位置，在进入右节点前，输出当前节点
    traverse(root.right);      // 进入右子树
    print(root.val)            // 在后序位置，离开后节点后，输出当前节点
}

这个代码的关键在于，时机。下图是可视化过程：

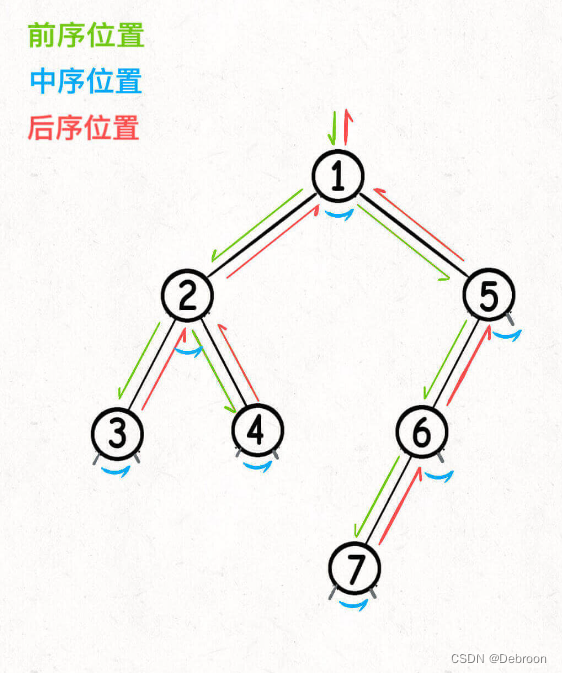
这里主要强调前序、后序的区别。

前序能解决的问题：遍历二叉树直接计算出来
后序能解决的问题：遍历二叉树直接计算出来，及遍历完子树之后才能计算出来。

递归函数，二叉树的每一个节点需要做什么（回溯模式、分解子问题模式），需要在什么时候（前\中\后序）做。

回溯模式

使用场景：问题可通过遍历一棵二叉树得到答案。

ans = []
void recall( 路径，[选择列表] )
	if 满足结束条件：
		ans.add( 路径 )
		return
		
	for 选择 in [选择列表]：
		做选择
		recall( 路径，[选择列表] )
		撤销选择

回溯框架，本质是遍历一颗决策树。

路径：已经做出的选择
选择列表：当前可以做的选择
结束条件：到了决策树底层，无法再做选择

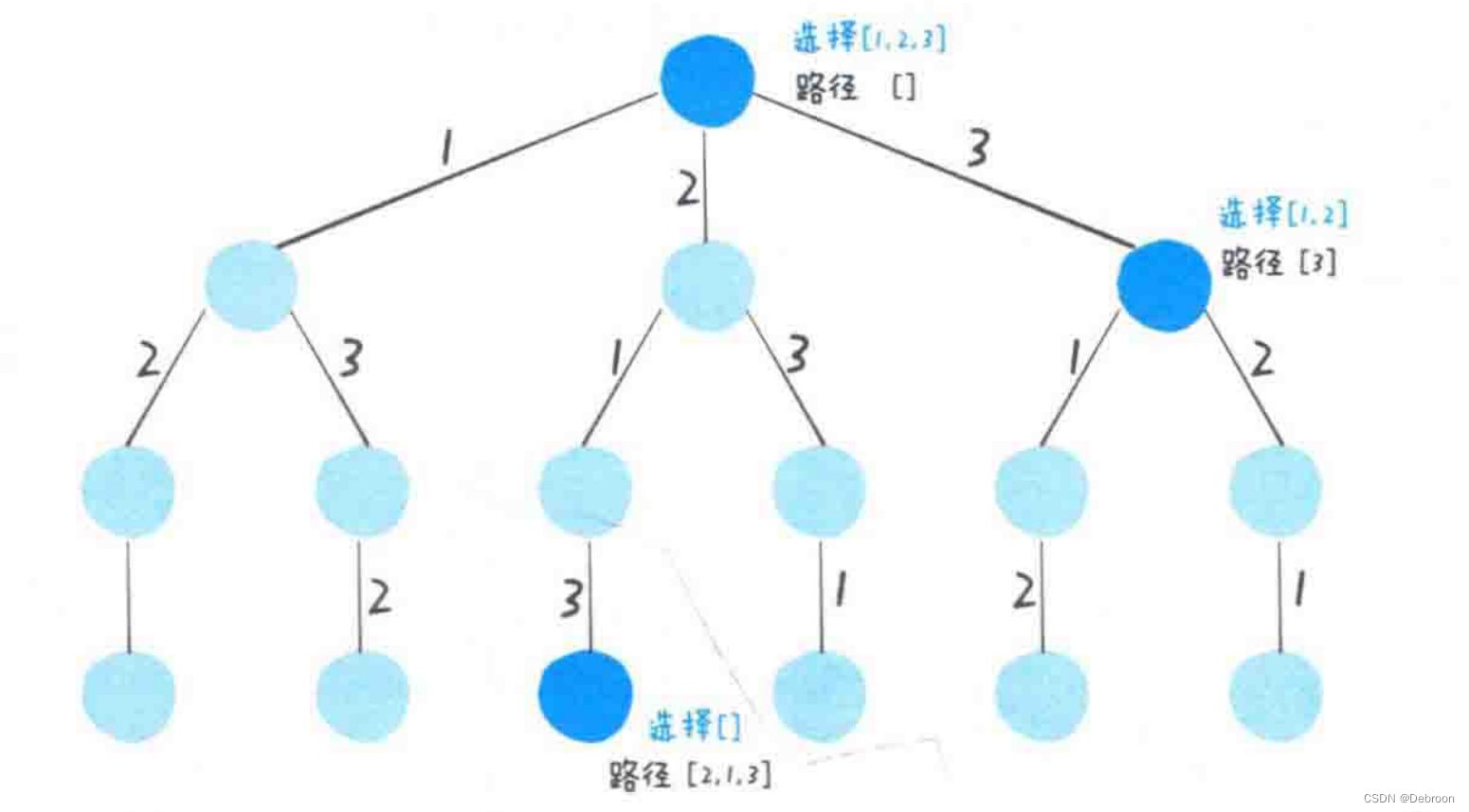
核心在于 for 循环里面的递归，在递归之前做选择，在递归之后撤销选择。

for 循环，如果可视化就是在遍历一颗 N 叉树

问题是，选择和撤销选择是在这颗树上做什么呢？

选择：是在这棵树上做前序遍历
撤销选择：是在这颗树上做后序遍历

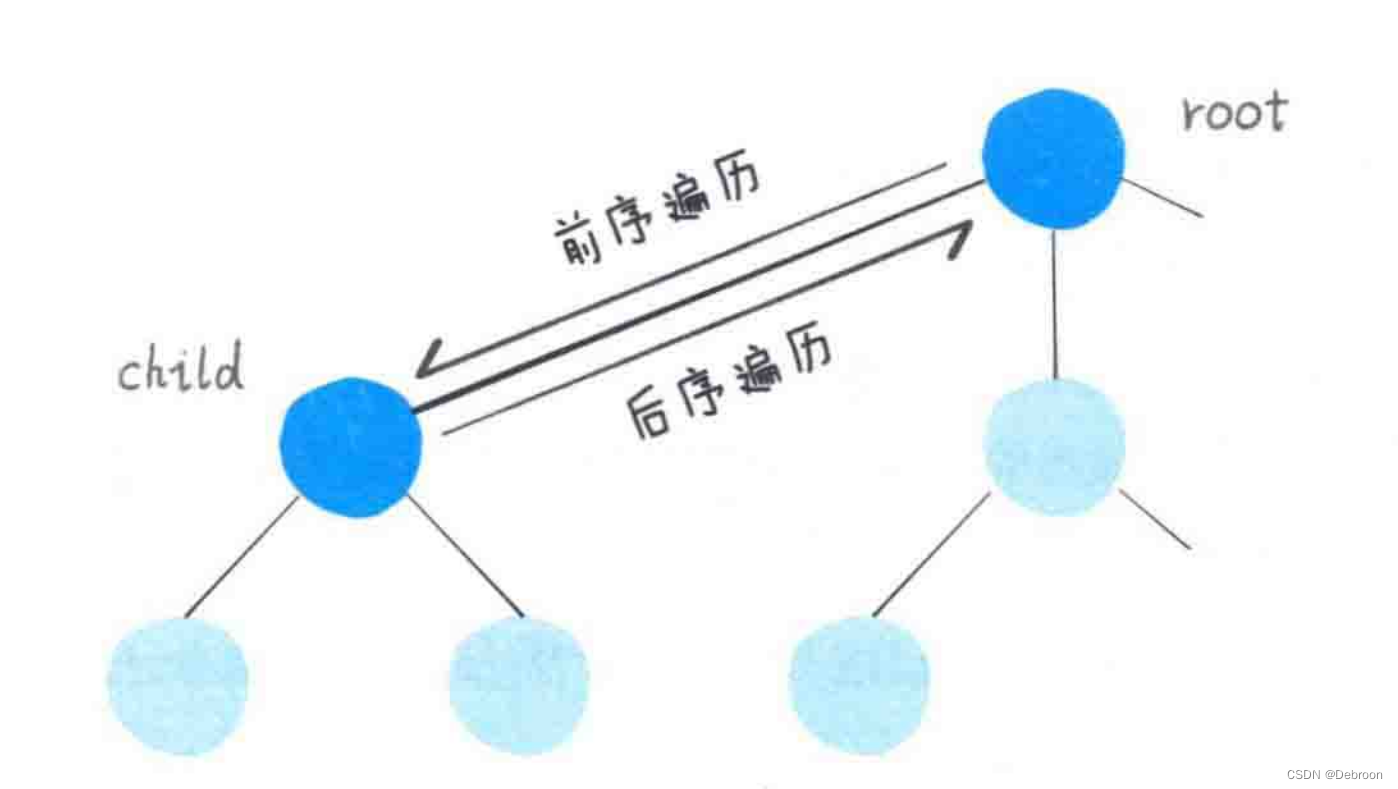
选择是，在进入树的某一节点前执行。

撤销选择是，在离开树的某一节点后执行。

做选择：在进入节点前，从选择列表拿出一个选择，将它放入路径。

撤销选择：在离开节点后，从路径中拿出一个选择，将它恢复到选择列表中。

子问题分解模式

使用场景：可通过子问题/子树的答案推导出原问题的答案。

原问题，分解成当前节点 + 左右子树的子问题。

int dp(TreeNode root) {        // 版本一
    if (root == null) 
		return 0;
		
    // 分解（子问题的规模为n/2，求出前半部分的最值，和后半部分的最值）
    int left = dp(root.left);
	int right = dp(root.right);
 
    // 合并（在把前半部分的最值和后半部分的最值做个比较，相当于求整个大数组的最值）
    return 最值(left, right);
}

int dp(int arr[], 某状态) {    // 版本二
    for 选择 in [选择列表]：
        res = 最值(res, dp(arr, 某状态));
    return res
}