Java-数据结构-二叉树＜三＞

承接上文：

Java-数据结构-二叉树＜一＞

Java-数据结构-二叉树＜二＞

一. 二叉树的简单介绍

见Java-数据结构-二叉树＜一＞

二. 二叉树的典型代码实现

见Java-数据结构-二叉树＜一＞

三. 二叉树的遍历

见Java-数据结构-二叉树＜一＞

四. leetcode实战

1~11 见 Java-数据结构-二叉树＜一＞，＜二＞

12. leetcode 剑指 Offer 54. 二叉搜索树的第k大节点

给定一棵二叉搜索树，请找出其中第 k 大的节点的值。
输入: root = [3,1,4,null,2], k = 1
3
/ \
1 4
\
2
输出: 4

【1】：

class Solution {
    int k;
    int ans;
    public int kthLargest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return ans;
    }
    public void dfs(TreeNode root){
        if(root == null) return;
        dfs(root.right);
        k--;
        if(k == 0){
            ans =  root.val;
            return;
        }
        dfs(root.left);
    }
}

本题要点：（1）右根左

（2）变量提出来

（3）如果k放到参数中，每个递归函数中的 k 都是独立的（k 是数字，传入函数是值传递），这样的话只要回溯就会出错~

13. leetcode236 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null) return null;
        if(q == root || p == root) return root;
        TreeNode left = lowestCommonAncestor(root.left, p,q);
        TreeNode right = lowestCommonAncestor(root.right, p,q);
        if(left == null && right != null) return right;
        if(left != null && right == null) return left;
        if(left != null && right != null) return root;
        return null;
    }
}

本题要点：

        退出条件
        1. root == null
        2. p,q中的任一一个为根节点
        单层逻辑

        1. 检查p,q能否在root.left中找到
        2. 检查p,q能否在root.right中找到
        3. 若1满足，2不满足，则最近公共节点为root.left
        4. 若1不满足，2满足，则最近公共节点为root.right
        5. 若1满足&2满足，则最近公共节点为root

14. leetcode653 两数之和 IV - 输入二叉搜索树

给定一个二叉搜索树 root 和一个目标结果 k，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

输入: root = [5,3,6,2,4,null,7], k = 9
输出: true

【2】：

class Solution {
    HashSet<Integer> set = new HashSet<>();
    public boolean findTarget(TreeNode root, int k) {
        if(root == null) return false;
        if(set.contains(k-root.val)) return true;
        set.add(root.val);
        return findTarget(root.left,k) || findTarget(root.right, k);
    }
    
}

本题要点：（1）用HashSet保存走过的路径的值，节省时间

15. leetcode102 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> list = new ArrayList<>();
        if(root == null) return list;
        Deque<TreeNode> queue = new ArrayDeque<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> temp = new ArrayList<>();
            int len = queue.size();
            for(int i = 0; i < len; i++){
                root = queue.poll();
                temp.add(root.val);
                if(root.left != null){
                    queue.add(root.left);
                }
                if(root.right != null){
                    queue.add(root.right);
                }
            }
            list.add(temp);
        }
        return list;
    }
}

【X0】特别的：
BFS 遍历使用队列数据结构：

void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // Java 的 pop 写作 poll()
        if (node.left != null) {
            queue.add(node.left);
        }
        if (node.right != null) {
            queue.add(node.right);
        }
    }
}

根据上述代码做出的结果是层序遍历是一维结构，而层序遍历要求我们区分每一层，也就是返回一个二维数组。在每一层遍历开始前，先记录队列中的结点数量 n（也就是这一层的结点数量），然后一口气处理完这一层的 n 个结点。

// 二叉树的层序遍历
void bfs(TreeNode root) {
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int n = queue.size();
        for (int i = 0; i < n; i++) { 
            // 变量 i 无实际意义，只是为了循环 n 次
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }
}

本题要点：（1）len的取值是为了知道上层有多少节点，用于分层

16. leetcode105 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

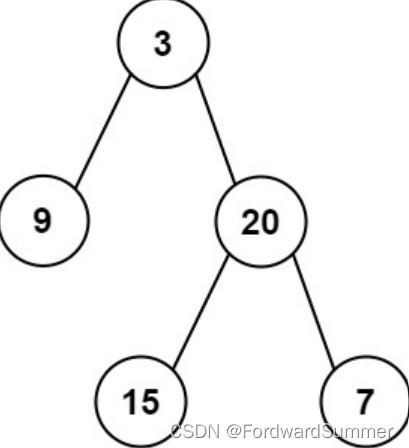
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

【C0】：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder.length < 1) return null;
        return helper(preorder,0,preorder.length,inorder,0,inorder.length);
    }
    public TreeNode helper(int[] preorder,int pleft, int pright, int[] inorder, int ileft, int iright){
        //左实右虚 到终点返回null
        if(pleft == pright){
            return null;
        }
        //构建根节点，根据前序遍历，根节点就是前序遍历的左边的元素
        TreeNode root = new TreeNode(preorder[pleft]);
        //用index来遍历在中序中的位置 找到对应的和前序最左节点的元素
        int index = 0;
        //index代表inorder中根节点的位置
        for(int i = ileft; i < iright; i++){
            if(preorder[pleft] == inorder[i]){
                index = i;
                break;
            }
        }
        // leftnum代表左子树的长度
        int leftnum = index - ileft;
        //递归建立左子树
        root.left = helper(preorder,pleft+1,pleft+leftnum+1,inorder,ileft,index);
        //递归建立左子树
        root.right = helper(preorder,pleft+leftnum+1,pright,inorder,index+1,iright);
        return root;
    }
}
// 前序 根 左 右
// 中序 左 根 右

本题要点：（1）在此种方法中，最重要的是找到根据前序遍历找到根节点的对应在中序遍历的位置，那么早在中序遍历中根节点左边为左子树，根节点右边为右子树

（2）接下来就要去寻找最为重要的左子树的起始和终点位置，右子树同理

（3）例如：

10
/ \
8 12
/ \ / \
5 9 11 13
/ \
3 6

前序遍历： [10, 8,5,3,6,9 , 12,11,13]
| \______/ \____/
根左右

中序遍历： [3,6,5,9,8, 10, 11,13,12 ]
\______/ | \____/
左根右

17. leetcode654 最大二叉树

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。递归地在最大值左边的子数组前缀上构建左子树。递归地在最大值右边的子数组后缀上构建右子树。返回 nums 构建的最大二叉树。

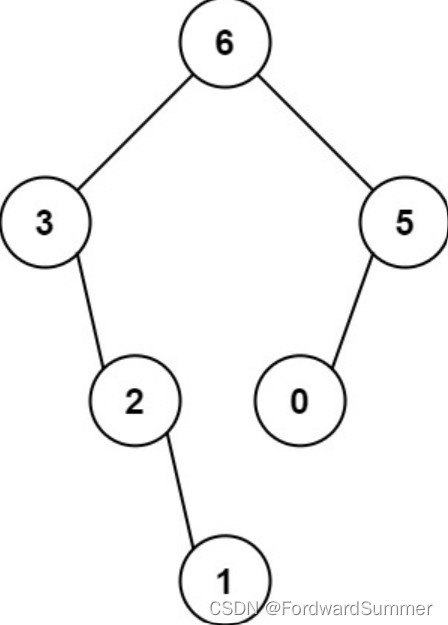
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 空数组，无子节点。
- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
- 空数组，无子节点。
- 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
- 只有一个元素，所以子节点是一个值为 0 的节点。
- 空数组，无子节点。

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return createTreeNode(nums,0,nums.length-1);
    }
    public TreeNode createTreeNode(int[] nums, int left, int right){
        if(left > right){
            return null;
        }
        int max = nums[left];
        int index = left;
        for(int i = left; i <= right; i++){
            if(nums[i] > max){
                max = nums[i];
                index = i;
            }
        }
        TreeNode mid = new TreeNode(max);
        mid.left = createTreeNode(nums,left,index-1);
        mid.right = createTreeNode(nums,index+1,right);
        return mid;
    }
}

本题要点：（1）在一段递归中，找到限定区间内的最大值，即是root节点

（2）形成root节点对应的位置为分界点，左半边的最大值是左子节点，右半边的最大值是右子节点。

（3）此题需要left>right，否则叶子节点的子节点构建不成功

18. leetcode96 不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种？返回满足题意的二叉搜索树的种数。

输入：n = 3
输出：5

class Solution {
    public int numTrees(int n) {
        if(n == 0 || n == 1) return 1;
        int sum = 0;
        for(int i = 1; i <= n; i++){
            int left = numTrees(i-1);
            int right = numTrees(n-i);
            sum += left*right;
        } 
        return sum;
    }
}

动态规划版

class Solution {
   public int numTrees(int n) {
        int[] dp = new int[n+1];
        dp[0] = 1;
        dp[1] = 1; 
        for(int i = 2; i <= n; i++){
            for(int j = 1; j<= i; j++){
                dp[i] += dp[j-1]*dp[i-j];
            }
        } 
        return dp[n];
    }
}

本题要点：（1）在一次遍历中，走到第i个，那么第i个就是根节点

（2）处理根节点的左半边，就是i-1个，处理根节点的右半边就是n-(i-1)-1个

（3）处理顺序： [1,2,3,4,5, 6, 7,8, 9]
\______/ | \____/
左根(i) 右

19. leetcode95 不同的二叉搜索树 II

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同二叉搜索树。可以按任意顺序返回答案。

输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

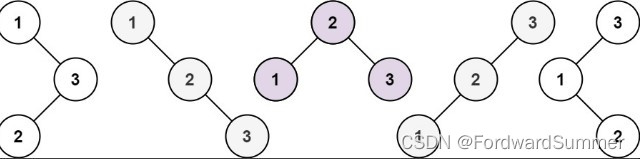
【C1】：

class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n < 1)
            return new ArrayList<>();
        return helper(1, n);
    }

    public List<TreeNode> helper(int start, int end){
        List<TreeNode> list = new ArrayList<>();

        if(start > end){
            // 如果一颗树的左子树为空，右子树不为空，要正确构建所有树，
            // 依赖于对左右子树列表的遍历，也就是下面两层for循环的地方，
            // 如果其中一个列表为空，那么循环都将无法进行。

            list.add(null);
            return list;
        }

        for(int i = start; i <= end; i++){
            // TreeNode root = new TreeNode(i);
            //这行代码放置在注释的地方，会造成一个问题，就是以当前为root根结点的树个数就
            //num = left.size() * right.size() > 1时，num棵子树会共用这个root结点，
            //在下面两层for循环中，root的左右子树一直在更新，如果每次不新建一个root，
            //就会导致num个root为根节点的树都相同。

            List<TreeNode> left = helper(start, i-1);  
            List<TreeNode> right = helper(i+1, end); 

            // 固定左孩子，遍历右孩子
            for(TreeNode l : left){
                for(TreeNode r : right){
                    TreeNode root = new TreeNode(i);
                    root.left = l;
                    root.right = r;
                    list.add(root);
                }
            }
        }
        return list;
    }
}

本题要点：（1）如何处理左右节点，即找到根节点，建立根节点，如何将根节点和左右节点连接在一起，接着，如何只添加一棵树的根节点。

（2）递归构建左子树，并拿到左子树所有可能的根结点列表left，右树相同

（3）左右子树都是各不相同的，因为根结点不同，固定左子节点，遍历右半边

20. leetcode515 在每个树行中找最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        Deque<TreeNode> queue = new ArrayDeque<>();
        if(root != null){
            queue.add(root);
        }
        while(!queue.isEmpty()){
            List<Integer> list = new ArrayList<>();
            int n = queue.size();
            int max = Integer.MIN_VALUE;
            for(int i = 0; i < n; i++){
                TreeNode node = queue.poll();
                max = Math.max(max,node.val);
                if(node.left != null){
                    queue.add(node.left);  
                }
                if(node.right != null){
                    queue.add(node.right);
                }
            }
            ans.add(max);
        }
        return ans;
    }
}

本题要点：（1）此题的本质是二叉树的层序遍历，是15题的应用

（2）在每一层保存一个最值，初始化为Integer.MIN_VALUE，依次更新，最后添加到最后的答案中

21. leetcode 剑指 Offer 33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

5
/ \
2 6
/ \
1 3

示例 1：

输入: [1,6,3,2,5]
输出: false
示例 2：

输入: [1,3,2,6,5]
输出: true

【X1】：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
        return recur(postorder,0,postorder.length-1);
    }
    public boolean recur(int[] postorder, int left, int right){
        if(left >= right) return true;
        int mid = left;
        while(postorder[mid] < postorder[right]) mid++;
        int cur = mid;
        while(cur < right){
            if(postorder[cur] < postorder[right]){
                return false;
            }
            cur++;
        }
        return recur(postorder,left,mid-1) && recur(postorder,mid,right-1);
    }
}

特别的【X2】：

先看一下一颗二叉树：

根
/ \
左右

中序遍历：左->根->右
后序遍历：左->右->根

只要是二叉搜索树就一定就满足：
左 < 根 && 右 > 根

在后序遍历也是要满足该特性。那么只要在后序遍历中找到对应的根左右三个节点来对比是否满足就行。

如：

10
/ \
8 12
/ \ / \
5 9 11 13
/ \
3 6

后序遍历： [3,6,5,9,8, 11,13,12, 10]
\______/ \____/ |
左右根

如果左 < 根 && 右 > 根成立。那么就有：

左集里面的每一个节点值都小于根
右集里面的每一个节点值都大于根

本题要点：（1）在规定范围区间内，最右边即是根节点