数据结构 最短路径课设（源码+实验报告+视频讲解）（不要钱、用了自取）

news2024/11/15 8:42:08

XI`AN TECHNOLOGICAL UNIVERSITY

课程设计报告

实验课程名称   算法与数据结构   

专    业：         

班    级：              

姓    名：               

学    号：         

实验学时：                        

指导教师：                     

成    绩：                        

        

    2023    年  1  月 7  日

目录

一、实验报告

        一、绪论

        二、基本要求

        三、信息描述

        五、详细设计

        六、调试与测试：

        八、总结

 源码：

视频上传比较麻烦，需要的同学可以联系我

一、实验报告

一、绪论

迪杰特斯拉算法思想：

设G=（V,E）是一个带权有向图，把顶点集合V分成两组，求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径，就将加入到集合S中。直到全部顶点都加入到S中，算法就结束了）。第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点V到S中各顶点的最短路径长度大于从源点V到V中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从V到此顶点的最短路径长度，V中的顶点的距离是从V到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

二、基本要求

(1)设计最短路径，包含以下方面：

1、用邻接矩阵存储一张带权有向图。

2、对图进行从某一源点到其他各顶点的最短路径

3、输出最后结果（路径名称、路径长度）。

三、信息描述

邻接矩阵建立包括：用二维数组存储信息。没有直达路径的为无穷。

用循环来判断最小值。

最终结果用一维数组存储。D[]存放源点到其他顶点的最短路径的长度，P[]存放该顶点最短路径的前驱顶点下标，visit[]为访问标识。初始全部值设为F，先把源点的标识设为T，后面每找到一个源点到其余顶点的最短路径，就将该顶点下标对应的标识置为T。直到全部顶点执行完毕。

输出一维数组D[]和P[]，显示最终结果。

  • 总体设计

五、详细设计

  • 第一部分，进行对邻接矩阵的初始化，首先自己到自己的距离肯定为0，然后到其余结点初始化为MAX，然后通过一个for循环，对边进行数据存入，打印函数用来验证。

  • 第二部分对于结点类的创建（构造、拷贝构造、赋值运算符重载、比较方式的重载）类中存放每一个结点的下标、最短路径长度、前驱结点。

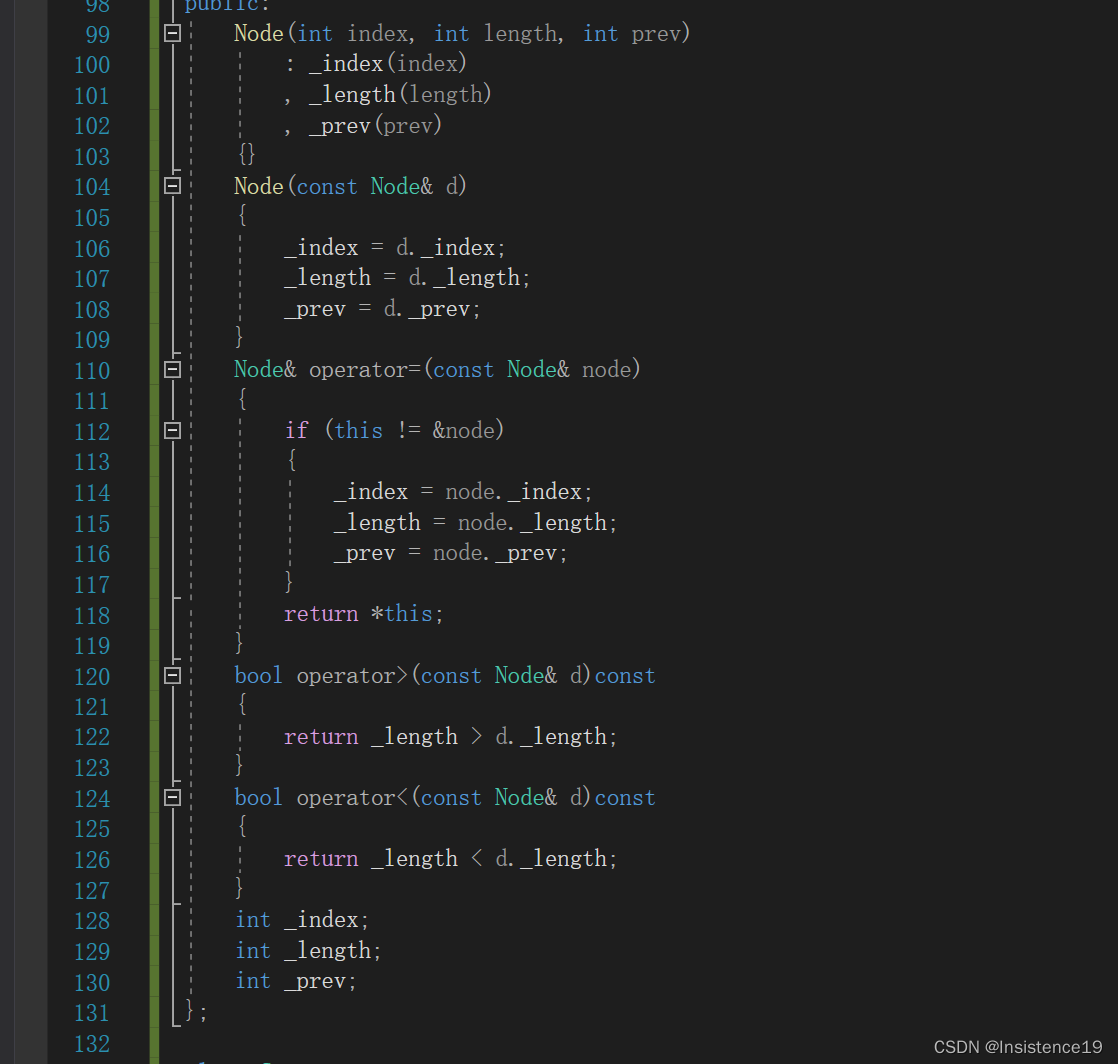
  •  第三部分：打印结果函数

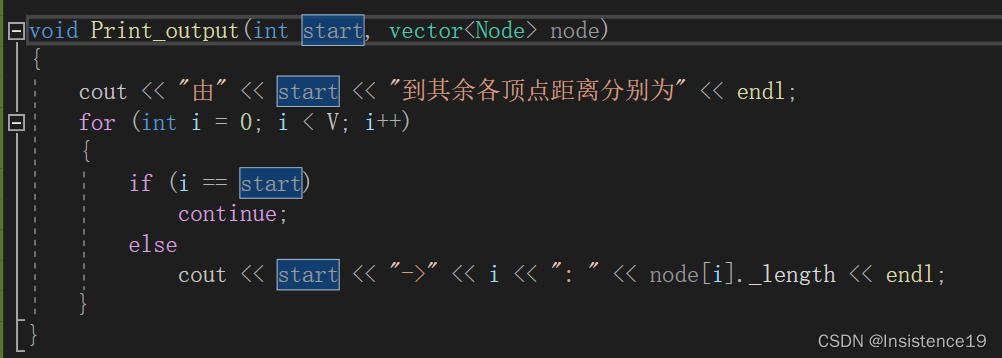
  •  迪杰斯特拉算法部分（核心）

完成好邻接矩阵的初始化工作以后，输入我们的起点坐标，对于起点来说，从起点到达起点的距离肯定是0，然后将起点坐标置入优先队列中，进入循环，循环退出条件是优先队列为空

每次取堆顶元素，使用cur进行保存，之后就将此结点pop

利用cur找出所有可以从cur出发到达的所有结点，将这些结点保存到集合S中，对于集合中的所有结点进行：

newlength = node[Index]._length + Graph[Index][back];

// 如果新距离小于cur之前的最小距离，就将cur重新赋值，并入队列

   if (newlength < node[back]._length)

   {

    node[back]._length = newlength;

    node[back]._prev = Index;

    q.push(node[back]);

   }

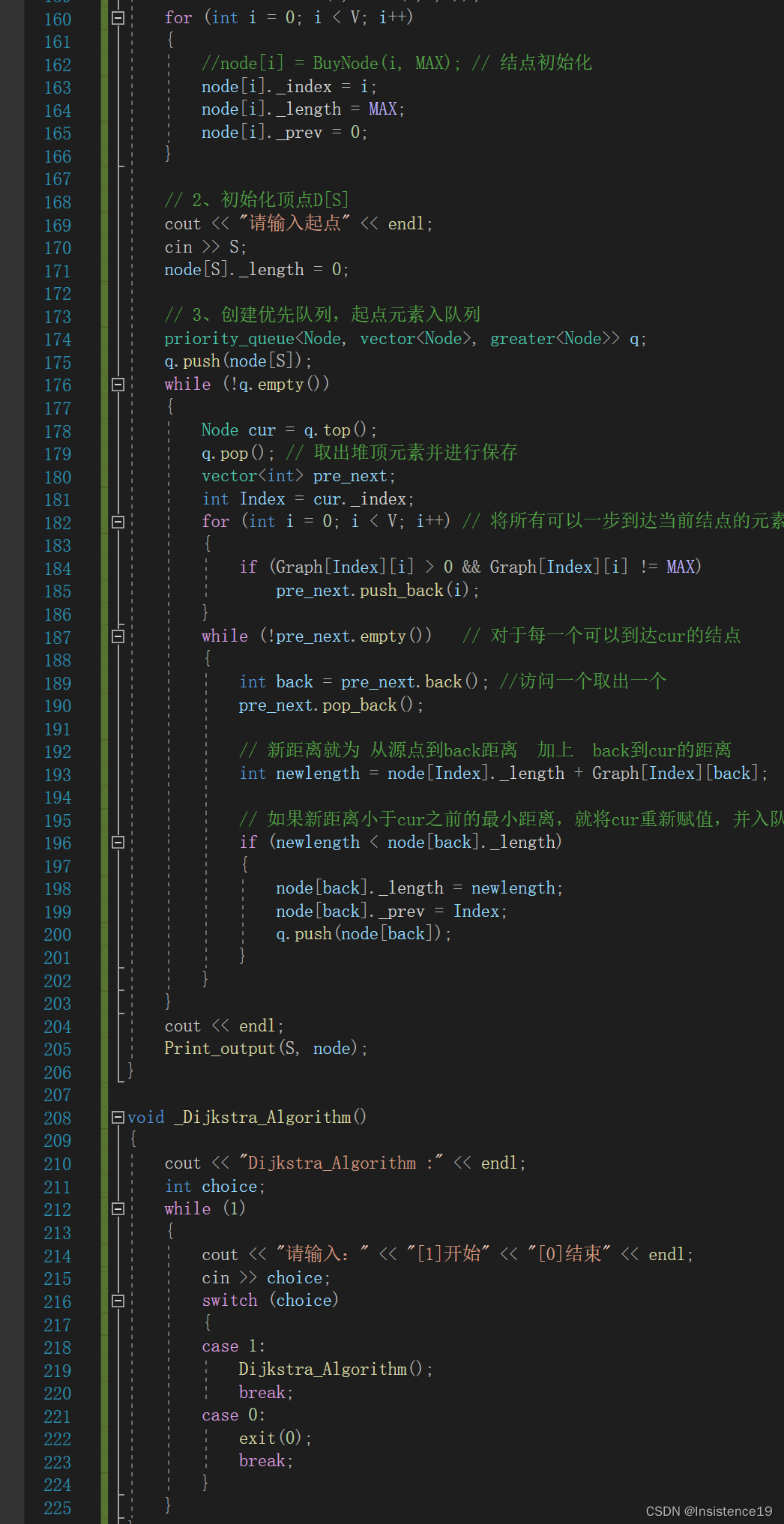
六、调试与测试：

在我写代码的时候大部分问题都可以查资料解决，如何使用vector,如果使用优先级队列，以及思路的来源也是借助于网上的资料查看，视频讲解，耗费时间最多的应该就是对于自定义类型优先级队列第三个参数比较方式的确定，本来我的代码是这样通过结构体与函数指针来实现，不过也出现了类型不匹配的问题，最后通过使用类中对比较关系的重载写出了bool类型关于>符号的重载（因为要建大堆）。

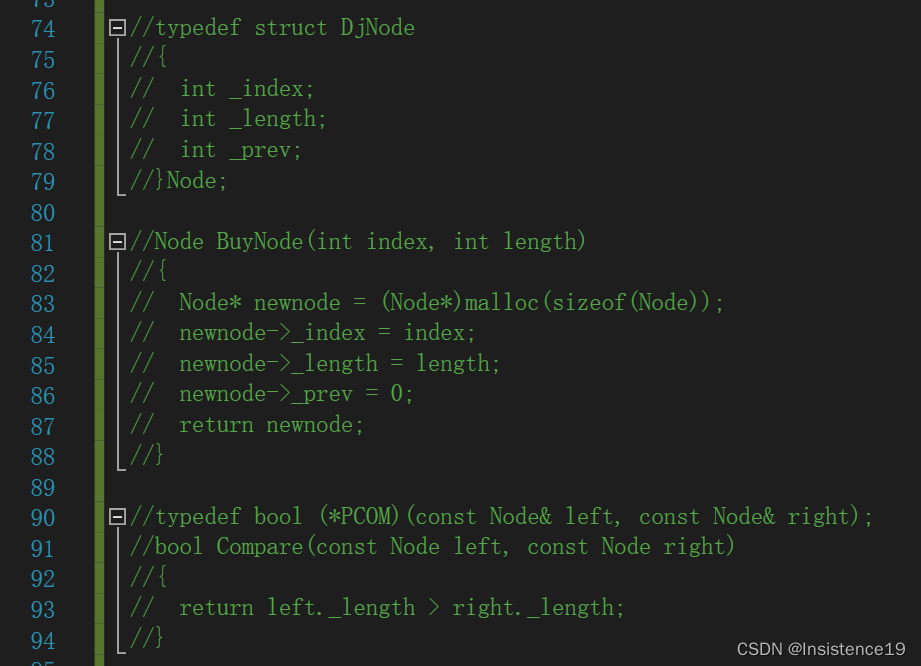
七、程序清单和执行结果：清单中应有足够的注释

运行结果：

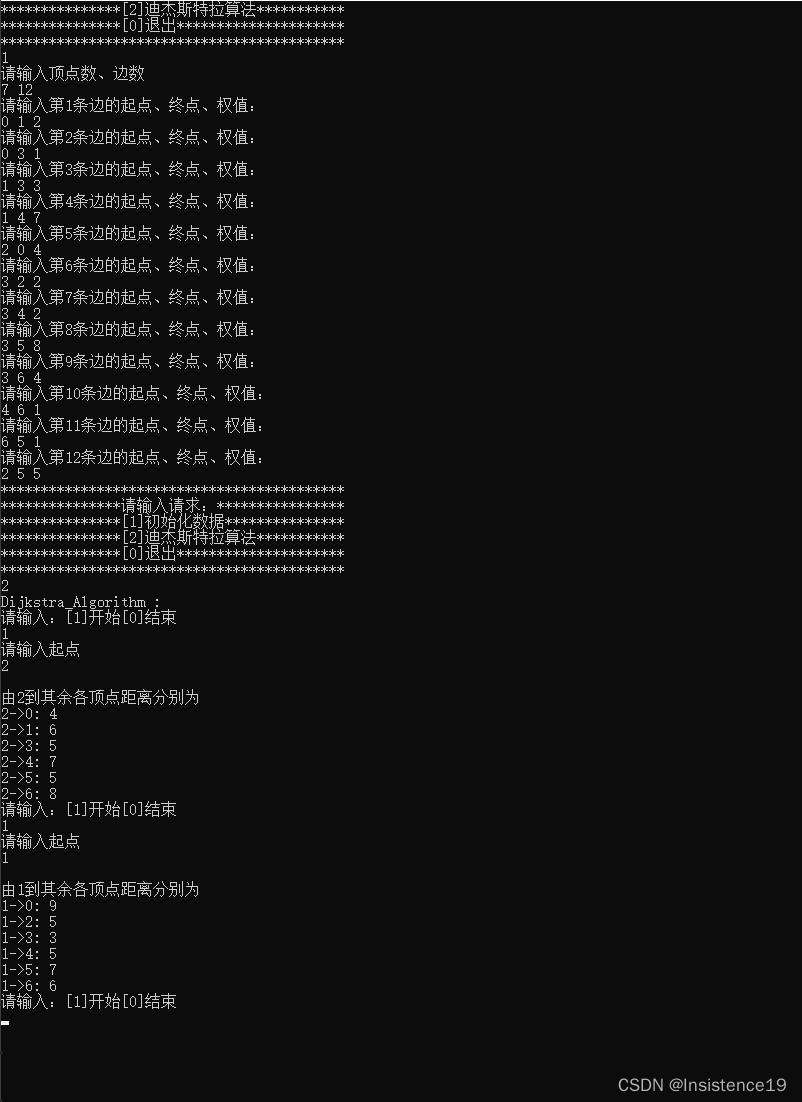
源码：

//(1)设计最短路径，包含以下方面:

//1、用邻接矩阵存储一张带权有向图。

//2、对图进行从某一源点到其他各顶点的最短路径

//了、输出最后结果(路径名称、路径长度)。

//三、信息描述

//邻接矩阵建立包括 : 用二维数组存储信息。没有直达路径的为无

//穷

//用循环来判断最小值

//最终结果用一维数组存储。D[]存放源点到其他顶点的最短路径的

//长度，P[]存放该顶点最短路径的前驱顶点下标

// 0 1 2   0 4 10  1 2 3  1 4 7  2 0 4  2 3 4  3 4 5  4 2 3

#include<functional>

#include<stdlib.h>

#include<iostream>

using namespace std;

#include<vector>

#include<queue>

#define MAX 1000 // 不可到达

int V, E, S; // 顶点数、边数、起点

vector<vector<int>> Graph;

void CreatMyGraph() // 初始化邻接矩阵

{

    cout << "请输入顶点数、边数" << endl;

    cin >> V >> E;

    Graph.resize(V);

    for (int i = 0; i < V; i++)

    {

        Graph[i].resize(V);

        for (int j = 0; j < V; j++)

        {

            if (i == j)

                Graph[i][j] = 0; // 自己到自己赋值为0

            else

                Graph[i][j] = MAX;   // 默认初始化到其余顶点均为MAX

        }

    }

    /*Graph[0][1] = 2;

    Graph[0][3] = 1;

    Graph[1][3] = 3;

    Graph[1][4] = 7;

    Graph[2][0] = 4;

    Graph[3][2] = 2;

    Graph[3][4] = 2;

    Graph[3][5] = 8;

    Graph[3][6] = 4;

    Graph[4][6] = 1;

    Graph[6][5] = 1;

    Graph[2][5] = 5;*/

    int begin, end;

    int length;

    for (int i = 0; i < E; i++)

    {

        cout << "请输入第" << i + 1 << "条边的起点、终点、权值：" << endl;

        cin >> begin >> end >> length;

        Graph[begin][end] = length;   // 初始化邻接矩阵

    }

}

void PrintMyGraph()

{

    cout << "图的邻接矩阵存储为：" << endl;

    for (int i = 0; i < V; i++)

    {

        for (int j = 0; j < V; j++)

        {

            cout << Graph[i][j] << " ";

        }

        cout << endl;

    }

}

//typedef struct DjNode

//{

//  int _index;

//  int _length;

//  int _prev;

//}Node;

//Node BuyNode(int index, int length)

//{

//  Node* newnode = (Node*)malloc(sizeof(Node));

//  newnode->_index = index;

//  newnode->_length = length;

//  newnode->_prev = 0;

//  return newnode;

//}

//typedef bool (*PCOM)(const Node& left, const Node& right);

//bool Compare(const Node left, const Node right)

//{

//  return left._length > right._length;

//}

class Node

{

public:

    Node(int index, int length, int prev)

        : _index(index)

        , _length(length)

        , _prev(prev)

    {}

    Node(const Node& d)

    {

        _index = d._index;

        _length = d._length;

        _prev = d._prev;

    }

    Node& operator=(const Node& node)

    {

        if (this != &node)

        {

            _index = node._index;

            _length = node._length;

            _prev = node._prev;

        }

        return *this;

    }

    bool operator>(const Node& d)const

    {

        return _length > d._length;

    }

    bool operator<(const Node& d)const

    {

        return _length < d._length;

    }

    int _index;

    int _length;

    int _prev;

};

class Com

{

public:

    bool operator()(const Node&left, const Node&right)const

    {

        return left._length > right._length;

    }

};

void Print_output(int start, vector<Node> node)

{

    cout << "由" << start << "到其余各顶点距离分别为" << endl;

    for (int i = 0; i < V; i++)

    {

        if (i == start)

            continue;

        else

            cout << start << "->" << i << ": " << node[i]._length << endl;

    }

}

void Dijkstra_Algorithm()

{

    // 1、初始化输出数组D、P

    //vector<int> D(V, MAX);  // 初始化最短长度数组D

    //vector<int> P(V, 0); // 初始化前驱结点数组P

    vector<Node> node(V, Node(0,0,0));

    for (int i = 0; i < V; i++)

    {

        //node[i] = BuyNode(i, MAX); // 结点初始化

        node[i]._index = i;

        node[i]._length = MAX;

        node[i]._prev = 0;

    }

    // 2、初始化顶点D[S]

    cout << "请输入起点" << endl;

    cin >> S;

    node[S]._length = 0;

    // 3、创建优先队列，起点元素入队列

    priority_queue<Node, vector<Node>, greater<Node>> q;

    q.push(node[S]);

    while (!q.empty())

    {

        Node cur = q.top();

        q.pop(); // 取出堆顶元素并进行保存

        vector<int> pre_next;

        int Index = cur._index;

        for (int i = 0; i < V; i++) // 将所有可以一步到达当前结点的元素下标全部保存到pre_next中

        {

            if (Graph[Index][i] > 0 && Graph[Index][i] != MAX)

                pre_next.push_back(i);

        }

        while (!pre_next.empty()) // 对于每一个可以到达cur的结点

        {

            int back = pre_next.back();   //访问一个取出一个

            pre_next.pop_back();

            // 新距离就为 从源点到back距离  加上  back到cur的距离

            int newlength = node[Index]._length + Graph[Index][back];

            // 如果新距离小于cur之前的最小距离，就将cur重新赋值，并入队列

            if (newlength < node[back]._length)

            {

                node[back]._length = newlength;

                node[back]._prev = Index;

                q.push(node[back]);

            }

        }

    }

    cout << endl;

    Print_output(S, node);

}

void _Dijkstra_Algorithm()

{

    cout << "Dijkstra_Algorithm :" << endl;

    int choice;

    while (1)

    {

        cout << "请输入：" << "[1]开始" << "[0]结束" << endl;

        cin >> choice;

        switch (choice)

        {

        case 1:

            Dijkstra_Algorithm();

            break;

        case 0:

            exit(0);

            break;

        }

    }

}

int main()

{

    int choice;

    while (1)

    {

        cout << "*******************************************" << endl;

        cout << "***************请输入请求：****************" << endl;

        cout << "***************[1]初始化数据***************" << endl;

        cout << "***************[2]迪杰斯特拉算法***********" << endl;

        cout << "***************[0]退出*********************" << endl;

        cout << "*******************************************" << endl;

        cin >> choice;

        switch (choice)

        {

        case 1:

            CreatMyGraph();

            break;

        case 2:

            _Dijkstra_Algorithm();

            break;

        case 0:

            exit(0);

            break;

        default:

            cout << "输入错误,请重新输入" << endl;

            break;

        }

    }

    return 0;

}

八、总结

通过这次课设，进一步提高了对于数据结构的认知，提升了自己的编程能力，了解了迪杰斯特拉算法在使用优先级队列来解决问题的便利之处。

 源码：

//(1)设计最短路径，包含以下方面:
//1、用邻接矩阵存储一张带权有向图。
//2、对图进行从某一源点到其他各顶点的最短路径
//了、输出最后结果(路径名称、路径长度)。
//三、信息描述
//邻接矩阵建立包括 : 用二维数组存储信息。没有直达路径的为无
//穷
//用循环来判断最小值
//最终结果用一维数组存储。D[]存放源点到其他顶点的最短路径的
//长度，P[]存放该顶点最短路径的前驱顶点下标
// 0 1 2   0 4 10  1 2 3  1 4 7  2 0 4  2 3 4  3 4 5  4 2 3
#include<functional>
#include<stdlib.h>
#include<iostream>
using namespace std;
#include<vector>
#include<queue>
#define MAX 1000 // 不可到达
int V, E, S; // 顶点数、边数、起点

vector<vector<int>> Graph;

void CreatMyGraph() // 初始化邻接矩阵
{
	cout << "请输入顶点数、边数" << endl;
	cin >> V >> E;
	Graph.resize(V);
	for (int i = 0; i < V; i++)
	{
		Graph[i].resize(V);
		for (int j = 0; j < V; j++)
		{
			if (i == j)
				Graph[i][j] = 0;	// 自己到自己赋值为0
			else
				Graph[i][j] = MAX;	// 默认初始化到其余顶点均为MAX
		}
	}
	/*Graph[0][1] = 2;
	Graph[0][3] = 1;
	Graph[1][3] = 3;
	Graph[1][4] = 7;
	Graph[2][0] = 4;
	Graph[3][2] = 2;
	Graph[3][4] = 2;
	Graph[3][5] = 8;
	Graph[3][6] = 4;
	Graph[4][6] = 1;
	Graph[6][5] = 1;
	Graph[2][5] = 5;*/
	int begin, end;
	int	length;
	for (int i = 0; i < E; i++)
	{
		cout << "请输入第" << i + 1 << "条边的起点、终点、权值：" << endl;
		cin >> begin >> end >> length;
		Graph[begin][end] = length;	// 初始化邻接矩阵
	}
}

void PrintMyGraph()
{
	cout << "图的邻接矩阵存储为：" << endl;
	for (int i = 0; i < V; i++)
	{
		for (int j = 0; j < V; j++)
		{
			cout << Graph[i][j] << " ";
		}
		cout << endl;
	}
}

//typedef struct DjNode
//{
//	int _index;
//	int _length;
//	int _prev;
//}Node;

//Node BuyNode(int index, int length)
//{
//	Node* newnode = (Node*)malloc(sizeof(Node));
//	newnode->_index = index;
//	newnode->_length = length;
//	newnode->_prev = 0;
//	return newnode;
//}

//typedef bool (*PCOM)(const Node& left, const Node& right);
//bool Compare(const Node left, const Node right)
//{
//	return left._length > right._length;
//}

class Node
{
public:
	Node(int index, int length, int prev)
		: _index(index)
		, _length(length)
		, _prev(prev)
	{}
	Node(const Node& d)
	{
		_index = d._index;
		_length = d._length;
		_prev = d._prev;
	}
	Node& operator=(const Node& node)
	{
		if (this != &node)
		{
			_index = node._index;
			_length = node._length;
			_prev = node._prev;
		}
		return *this;
	}
	bool operator>(const Node& d)const
	{
		return _length > d._length;
	}
	bool operator<(const Node& d)const
	{
		return _length < d._length;
	}
	int _index;
	int _length;
	int _prev;
};

class Com
{
public:
	bool operator()(const Node&left, const Node&right)const
	{
		return left._length > right._length;
	}
};

void Print_output(int start, vector<Node> node)
{
	cout << "由" << start << "到其余各顶点距离分别为" << endl;
	for (int i = 0; i < V; i++)
	{
		if (i == start)
			continue;
		else
			cout << start << "->" << i << ": " << node[i]._length << endl;
	}
}

void Dijkstra_Algorithm()
{
	// 1、初始化输出数组D、P
	//vector<int> D(V, MAX);	// 初始化最短长度数组D
	//vector<int> P(V, 0);	// 初始化前驱结点数组P
	vector<Node> node(V, Node(0,0,0));
	for (int i = 0; i < V; i++)
	{
		//node[i] = BuyNode(i, MAX); // 结点初始化
		node[i]._index = i;
		node[i]._length = MAX;
		node[i]._prev = 0;
	}

	// 2、初始化顶点D[S]
	cout << "请输入起点" << endl;
	cin >> S;
	node[S]._length = 0;

	// 3、创建优先队列，起点元素入队列
	priority_queue<Node, vector<Node>, greater<Node>> q; 
	q.push(node[S]);
	while (!q.empty())
	{
		Node cur = q.top();
		q.pop(); // 取出堆顶元素并进行保存
		vector<int> pre_next;
		int Index = cur._index;
		for (int i = 0; i < V; i++) // 将所有可以一步到达当前结点的元素下标全部保存到pre_next中
		{
			if (Graph[Index][i] > 0 && Graph[Index][i] != MAX)
				pre_next.push_back(i);
		}
		while (!pre_next.empty())	// 对于每一个可以到达cur的结点
		{
			int back = pre_next.back();	//访问一个取出一个
			pre_next.pop_back();

			// 新距离就为 从源点到back距离  加上  back到cur的距离
			int newlength = node[Index]._length + Graph[Index][back];

			// 如果新距离小于cur之前的最小距离，就将cur重新赋值，并入队列
			if (newlength < node[back]._length)
			{
				node[back]._length = newlength;
				node[back]._prev = Index;
				q.push(node[back]);
			}
		}
	}
	cout << endl;
	Print_output(S, node);
}

void _Dijkstra_Algorithm()
{
	cout << "Dijkstra_Algorithm :" << endl;
	int choice;
	while (1)
	{
		cout << "请输入：" << "[1]开始" << "[0]结束" << endl;
		cin >> choice;
		switch (choice)
		{
		case 1:
			Dijkstra_Algorithm();
			break;
		case 0:
			exit(0);
			break;
		}
	}
}

int main()
{
	int choice;
	while (1)
	{
		cout << "*******************************************" << endl;
		cout << "***************请输入请求：****************" << endl;
		cout << "***************[1]初始化数据***************" << endl;
		cout << "***************[2]迪杰斯特拉算法***********" << endl;
		cout << "***************[0]退出*********************" << endl;
		cout << "*******************************************" << endl;
		cin >> choice;
		switch (choice)
		{
		case 1:
			CreatMyGraph();
			break;
		case 2:
			_Dijkstra_Algorithm();
			break;
		case 0:
			exit(0);
			break;
		default:
			cout << "输入错误,请重新输入" << endl;
			break;
		}
	}
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/176727.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux Debian11安装QT6开发环境

Linux Debian11安装QT6开发环境

从Qt5.14开始&#xff0c;官方不提供离线安装包&#xff0c;只提供源码包和在线安装器。但是清华为我们提供了快速的在线安装方式。 一.下载清华提供的在线安装器 在线安装器下载链接 二、给在线安装器文件赋予执行权限 三、配置镜像地址运行安装器 清华源&#xff1a; ./…
阅读更多...
7.Java判断和循环+面试相关力扣算法题详解

7.Java判断和循环+面试相关力扣算法题详解

提示&#xff1a; 文章目录前言一、顺序结构二、分支语句(1)if语句(2)switch语句*default的位置和省略:*case穿透*switch新特性*switch和if的第三种格式各自的使用场景三、循环结构1.分类2.for循环3.while循环4.for和while的对比:5.for和while循环的区别:6.练习:四、面试时的两…
阅读更多...
【安卓】zoo for zotero WebDAV 自动论文同步笔记

【安卓】zoo for zotero WebDAV 自动论文同步笔记

前言 前言是我写这篇博客的动机&#xff0c;可以跳过直接从“准备”开始看 之前使用mendeley管理文献&#xff0c;它不仅可以同步文件&#xff0c;还跨平台&#xff08;win、安卓等&#xff09;。但是后面&#xff0c;mendeley停止了移动平台的支持&#xff0c;导致我不能用我…
阅读更多...
JQUERY案例

JQUERY案例

电梯导航 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-width, i…
阅读更多...
一、pyhon准备工作篇(黑马程序猿-python学习记录)

一、pyhon准备工作篇(黑马程序猿-python学习记录)

黑马程序猿的python学习视频&#xff1a;https://www.bilibili.com/video/BV1qW4y1a7fU/ 目录 1. python官网 2. 检查是否安装完毕 3. pycharm官网 5. phcharm更换主题 6. 新建第一个python文件 7. pycharm字体大小设置 ​​​​​​​8. 设置快捷键 设置字体大小 ​​​​​​…
阅读更多...
AJAX 简介

AJAX 简介

AJAX 是一种在无需重新加载整个网页的情况下&#xff0c;能够更新部分网页的技术。 AJAX 是什么&#xff1f; AJAX Asynchronous JavaScript and XML. AJAX 是一种用于创建快速动态网页的技术。 AJAX 通过在后台与服务器进行少量数据交换&#xff0c;使网页实现异步更新。这…
阅读更多...
第三章 关系数据库标准语言SQL

第三章 关系数据库标准语言SQL

第三章 关系数据库标准语言SQL 目录第三章 关系数据库标准语言SQL3.1 SQL概述3.1.1 产生与发展3.1.2 SQL的特点3.1.3 SQL的基本概念3.2 数据库实例3.3 数据定义3.3.1 模式的定义和删除3.2.2基本表的定义、删除和修改1.常见数据类型2.定义基本表3.修改基本表4.删除基本表5.模式和…
阅读更多...
2. 返回传播计算方法|神经网络整体架构|神经元个数对结果的影响|正则化与激活函数|神经网络过拟合解决方法

2. 返回传播计算方法|神经网络整体架构|神经元个数对结果的影响|正则化与激活函数|神经网络过拟合解决方法

文章目录返回传播计算方法神经网络整体架构&#xff08;暂时留存&#xff0c;等后面补&#xff09;神经元个数对结果的影响正则化与激活函数神经网络过拟合解决方法返回传播计算方法 实际上计算L&#xff08;损失值&#xff09;的时候并不是只是拿一组w来进行计算&#xff0c;…
阅读更多...
用过MyBatis-Plus，我再也不想用mybatis了——MyBatis-Plus快速入门加常见注解总结，一文快速掌握MyBatis-Plus

用过MyBatis-Plus，我再也不想用mybatis了——MyBatis-Plus快速入门加常见注解总结，一文快速掌握MyBatis-Plus

相比与mybatis只做增强&#xff0c;不做修改 MyBatis-Plus学习笔记一&#xff0c;是什么二&#xff0c;入门案例1.建库建表2.创建spring Boot工程3.配置相关包及类4.测试三&#xff0c;基本的curd1.BaseMapper2.通用Service四.常用注解1.TableName2.TableId3TableField4.TableL…
阅读更多...
【python】面向对象编程

【python】面向对象编程

文章目录一、函数大全1.1 匿名函数 lambda1.2 过滤函数 filter1.3 format1.4 try和except1.5 位置参数和关键字参数二、类与对象2.1创建对象2.2 封装的实现方式2.3 继承2.4方法重写2.5 object 类2.5.1 __str()__2.5.2 dict()2.5.3 len()2.5.4 add()2.5.5 new()init()2.6 多态的…
阅读更多...
初识C语言(下)

初识C语言(下)

写在前面 好了,现在我们开始C语言的第二个部分.今天我们需要看下面几个知识点,都是非常简单的,我们主要认识一下. 数组 我们知道一个一个属性可以用一个类型去表示,那么我想问的是如果是一个属性的多个呢?也就是多个一样的东西,此时我们就要使用数组来进行表示,所谓的数组就…
阅读更多...
22. 输入和输出

22. 输入和输出

1. 输出格式美化 (1) 如果你希望输出的形式更加多样&#xff0c;可以使用 str.format() 函数来格式化输出值。 (2) 如果你希望将输出的值转成字符串&#xff0c;可以使用 repr() 或 str() 函数来实现。   str()&#xff1a; 函数返回一个用户易读的表达形式。   repr()&am…
阅读更多...
产品原型设计方法

产品原型设计方法

产品原型设计方法1. 色彩选择与按钮设计1.1色彩选择1.2 按钮设计2. 使用原型设计中的基础元素2.1 使用文字元素2.2 使用图标元素3. 设计导航菜单栏和卡片式布局3.1设计导航菜单栏4.3 设计卡片式布局4. 使用UI框架4.1 使用UI框架的好处4.2 常用的UI框架1. 色彩选择与按钮设计 1…
阅读更多...
K8s:通过 kubectl 插件 Kubepug 实现集群升级检查(废弃API资源检查)

K8s:通过 kubectl 插件 Kubepug 实现集群升级检查(废弃API资源检查)

写在前面 分享一个小工具&#xff0c;可用于 版本升级的 废弃 API 对象检查博文内容涉及&#xff1a; kubepug 离线安装&#xff0c;配置 kubectl 插件kubepug 两种方式离线使用 Demo 理解不足小伙伴帮忙指正 昔我往矣&#xff0c;杨柳依依。今我来思&#xff0c;雨雪霏霏。 —…
阅读更多...
【HBase入门】1. HBase基础

【HBase入门】1. HBase基础

简介 Hadoop 从 1970 年开始&#xff0c;大多数的公司数据存储和维护使用的是关系型数据库大数据技术出现后&#xff0c;很多拥有海量数据的公司开始选择像Hadoop的方式来存储海量数据Hadoop使用分布式文件系统HDFS来存储海量数据&#xff0c;并使用 MapReduce 来处理。Hadoo…
阅读更多...
【Ajax】同源策略、跨域和JSONP

【Ajax】同源策略、跨域和JSONP

一、同源策略什么是同源如果两个页面的协议&#xff0c;域名和端口都相同&#xff0c;则两个页面具有相同的源。例如&#xff0c;下表给出了相对于 http://www.test.com/index.html 页面的同源检测&#xff08;如果没有写端口号&#xff0c;默认是80&#xff09;&#xff1a;UR…
阅读更多...
开篇点睛——Elasticsearch

开篇点睛——Elasticsearch

在互联网当中我们的查询的信息主要包括文章、视频、图片、网站信息等各式各样的复杂海量信息。怎么才能快速、准确的检索到我们想要的信息呢? 传统意义上根据数据的格式&#xff0c;我们会将数据分为三个大类 结构化数据非结构化数据半结构化数据 接下来我们详细的了解一下这…
阅读更多...
Day07 - 面向对象

Day07 - 面向对象

1. 面向对象概述 面向对象是一种对现实世界理解和抽象的方法&#xff0c;是计算机编程技术发展到一定阶段后的产物。 面向对象是相对于面向过程来讲的&#xff0c; 面向对象方法 &#xff0c;把相关的数据和方法组织为一个整体来看待&#xff0c;从更高的层次来进行系统建模&a…
阅读更多...
开发人员必备的 15 个备忘单

开发人员必备的 15 个备忘单

随着网络编程技术的快速发展&#xff0c;我们必须学习很多新东西。有些语言和框架非常复杂&#xff0c;您可能记不住所有的语法或方法。备忘单是易于访问的笔记。当有人在过去目睹任何有帮助或有价值的事情时&#xff0c;包括我自己&#xff0c;我们都会做笔记。但是&#xff0…
阅读更多...
Vue 快速入门(四)

Vue 快速入门(四)

前面已经介绍Vue常用指令的基本应用&#xff0c;这篇介绍Vue的一些特殊属性的使用。 01 - 计算属性Computed 计算属性关键词&#xff1a;Computed。 计算属性在处理一些复杂逻辑时是很有用的。 普通的写法 比如字符串反转普通写法&#xff0c;如下&#xff1a; <!DOCTYPE h…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023