概述

• 数据是信息的载体，是描述客观师傅属性的数、字符以及所有能输入到计算机中并被计算机程序识别和处理的符号的集合
• 数据是计算机程序加工的原料
• 计算机可以识别和处理的，只有二进制数
• 数据元素是数据的基本单位，通常作为一个整体进行考虑和处理
• 一个数据元素可以由若干数据项组成，数据项是构成数据元素的不可分割的最小的单位
• • 例如APP个人中心就是一个数据元素，元素中包含的昵称，名称等就是一个个的数据项
• 数据结构就是相互之间存在一种或者多种特定关系的数据元素的集合
• • 简单的说，我们如果要解决某个问题，就需要保存一组数据，如何让将
• 数据对象是具有相同性质的数据元素的集合，是数据的一个子集
• 数据结构的三要素：逻辑结构、物理结构和数据的运算
• • 逻辑结构指的是：数据元素之间的逻辑关系，分为集合、线性结构、树形结构和图状结构（网状结构）
• • 集合：各个元素同属于一个集合，没有其他关系
• • 线性结构：数据元素之间一对一的关系，除了第一个元素，所有的元素都有唯一的前驱；除了最后一个元素，所有的元素都有唯一的后继
• • 树形结构：元素之间是一对多的关系（父子结构）
• • 图状结构：数据元素之间是多对多的关系
• 数据的存储结构：用计算机表示数据元素的逻辑关系的方式，存储方式分为：顺序存储、链式存储、索引存储和散列存储，就 线性结构而言：
• • 顺序存储：将逻辑上相邻的元素存储在屋里位置上也相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。采用这种方式存储时会分配连续的存储空间
• • 链式存储：逻辑上相邻的元素在屋里位置上可以不相邻，借助指示元素的指针来表示元素之间的关系（用指针指向下一个元素的存储位置）
• • 索引存储：在存储元素信息的同时，还建立附加索引表，索引表的每项称为索引项，索引项的一般形式时关键字和地址
• • 散列存储：根据元素的关键字直接计算出该元素的存储位置，又称为哈希存储
• • 因此，链式、索引和散列可以称为非顺序存储
• • 如果采用顺序存储，那么每个元素在物理上必须时连续的
• • 如果采用非顺序存储，则各个元素在物理上可以是离散的
• • 数据的存储结构，会影响存储空间分配的方便程度
• • 数据的存储结构，会影响对数据运算的速度
• 数据的运算：运算的定义是针对逻辑结构的，指出运算的功能；运算的实现是针对存储结构的，指出运算的具体操作步骤
• 数据类型：是一个值的集合和定义在此集合上的一组操作的总称
• • 原子类型：其值不可再分的数据类型，例如int、bool等
• • 结构类型：他的值可以再分解为若干成分（分量）的数据类型，例如函数
• 抽象数据类型（ADT）：是抽象数据组织及与之相关的操作
• • 简单的说，就是将一个数据模型以及定义在此数学模型上的一组操作
• • 即将数据类型和数据类型上的运算困在一起，进行封装
• • 引入抽象数据类型的目的是将数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使他们相互独立，即实现方式和引用隔离开
• • 封装后，最常使用的数据运算有五种：插入、删除、修改、查找和排序

数据结构

• 我们为了解决某个问题，就需要将数据保存下来，然后根据数据的存储方式来设计算法实现进行处理，因为数据存储方法的不同就需要不同的算法
• • 我们如果希望问题解决的速度快，就需要研究如何保存数据，这就是数据结构
• • 数据结构解决的就是一组数据如何保存，保存形式时怎样的问题
• 数据是一个抽象的概念，将其进行哈分类之后得到程序语言中的基本类型，例如：int，float，char等
• 数据元素之间并不是独立的，存在特定的关系
• 数据结构指数据对象中，数据元素之间的关系，数据结构就是对数据基本类型的一次封装
• python中提供了很多现成的数据结构类型，即内置数据结构，例如列表、字典、远足等
• 还有需要我们自己去定义实现的数据组织方式，这种组织方式称为python的扩展数据结构，例如栈和队列

算法

• 程序= 数据结构+算法
• • 数据结构考虑如何将现实世界的问题信息化，将信息存进计算机，同时还要实现对数据结构的基本操作
• • 算法：如何处理这些信息，以解决实际问题
• 算法的特性：
• • 有穷性：一个算法总在执行有穷之后结束，且每一步都可在有穷的时间内完成，算法必须是有穷的，但是程序可以是无穷的
• • 确定性：算法中每条这令必须有确切的含义，没有二义性，对于相同的输入只能得出相同的输出
• • 可行性：算法中描述的操作都可以痛殴已经实现的基本运算执行优先次来实现
• • 输入：一个算法有0个或者多个输出，这些输入取自于某个特定的对象的集合
• • 输出，一个算法有一个或者多个输出。这些输出是与输入有着某种特定关系的量
• 一个好的算法，设计是要尽量追求目标，他有以下特质：
• • 正确性：算法应该能够正确的解决问题
• • 可读性：算法应具备良好的可读性，以帮助人们理解
• • • 算法可以用伪代码描述，甚至用文字描述，重要的是要无歧义的描述出解决问题的步骤
• • 健壮性：输入非法数据时，算法能适当的做出反应货进行处理，而不会莫名其妙的输出结果
• • 高效率和低存储量的需求，即执行速度快，时间复杂度低和不废内存，空间复杂度低
• 算法和数据结构的区别：
• • 数据结构只是静态的描述了数据元素之间的关系
• • 高效的成宿需要在数据结构的基础上设计和选择算法
• • 简单的说：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题的载体

时间复杂度

• 时间复杂度：用于评价一个算法的时间开销，也可以理解为事前预估算法时间开销T(n)和问题规模n之间的关系
• 一般情况下，时间复杂度只取最高级
• 时间复杂度的大小顺序为：O(1)<O(logN)<O(n)<O(nlogN)<O(n的平方)<O(n的三次方)<O(2的n次方)<O(n的阶乘)<O(n的n次方)
• 简单的来说，就是常对幂指阶（从小到大）
• 代码执行时，顺序执行的代码只会影响常数，可以忽略
• • 只需要挑选循环中的基本操作，分析他的执行次数与n的关系即可
• • 如果有多层前套循环，只需要关注最深层的循环，他循环了几次
• 分析算法的时候，存在集中考虑：
• • 算法完成工作最少需要的时间复杂度，叫做最优时间复杂度
• • 算法完成工作最多需要的时间复杂度，叫做最坏时间复杂度
• • 算法完成工作平均需要多少时间，即平均复杂度
• 例如以下代码，如果查找的元素为第一个，就是最优复杂度；如果要查找的元素为最后一个就是最坏时间复杂度；每个元素平均多久可以找到，就是平均复杂度

list_data = ['hfdgj',8.0,33,"jdjf",6,3,7]
for i in list_data:
    if i==7:
        print("pass")
        break

• 时间复杂度的计算
• • 1.基本操作：即常数项，认为其时间复杂度为O(1)，例如循环体中的变量定义，if语句中的每个条件等
• • 2.顺序结构：时间复杂度按照加法进行计算
• • 3.循环结构：时间复杂度按照乘法进行计算
• • 4.分支结构（条件）：时间复杂度取最大值
• • 5.判断一个算法的时间效率时，往往只需要关注操作数量的最高次项，其他次项和常数项可以忽略
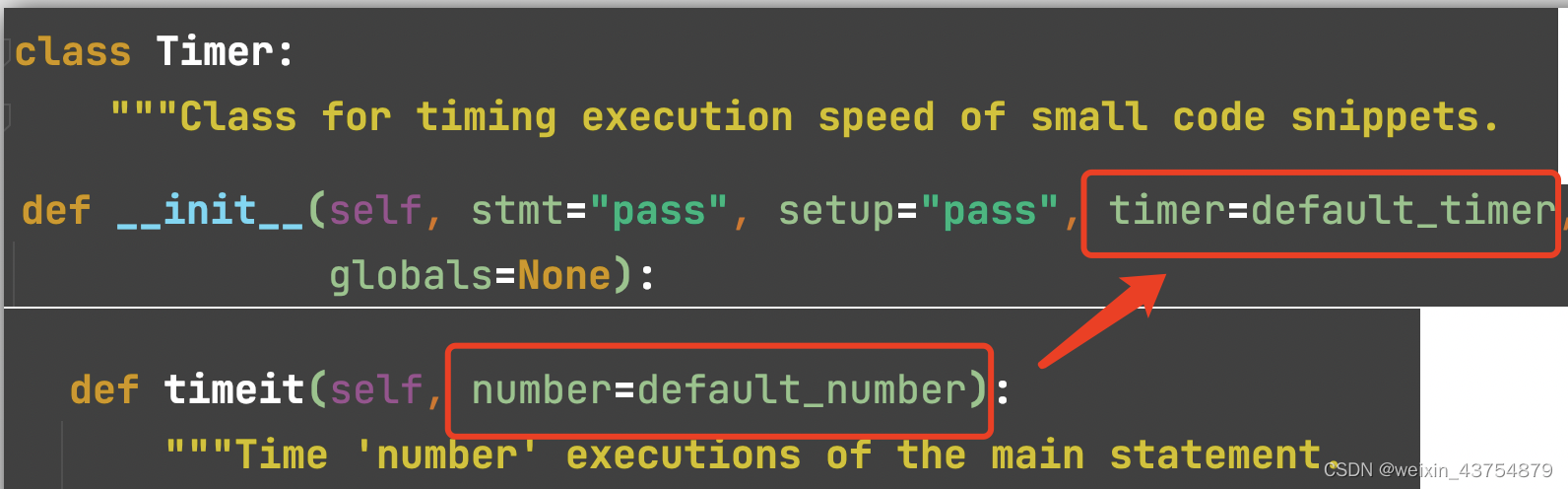
• • 6.在没有特殊说明时，我们所分析的算法的时间复杂度应指向最坏时间复杂度

python的代码执行时间测量模块

• 模块名：timeit
• 首先要导入第三方模块，from timeit import Timer，Timer中需要传入几个参数，因为有初始化的存在，如下图示：
  
• 其中：stmt:参数是要测试的代码语句
• setup：参数是运行代码时需要的设置
• timer 和number是一个含义，运行的次数，其返回的时间为运行之后的平均值
• 因此在调用这个类时，需要传两个参数
• 代码编写及执行结果如下：

from timeit import Timer

def t1():
    data = []
    for i in range(10000):
        data.extend([i])
def t2():
    data =[i for i in range(10000)]
def t3():
    data = []
    for i in range(10000):
        data=data+[i]
def t4():
    data = []
    for i in range(10000):
        data.insert(0,1)
def t5():
    data = []
    for i in range(10000):
        data.append(i)
a = Timer("t1()","from __main__ import t1")
a_time = a.timeit(100)
b = Timer("t2()","from __main__ import t2")
b_time = b.timeit(100)
c = Timer("t3()","from __main__ import t3")
c_time = c.timeit(100)
d = Timer("t4()","from __main__ import t4")
d_time = d.timeit(100)
e = Timer("t5()","from __main__ import t5")
e_time = e.timeit(100)
print("extend:",a_time,"\n迭代器:",b_time,"\n+:",c_time)
print("append:",e_time,"\ninsert:",d_time)
-------------------------run_result----------------------
extend: 0.05123333399751573 
迭代器: 0.013302958999702241 
+: 8.697985875001905
append: 0.028532749998703366 
insert: 2.6066741249996994

• list函数中，常见内置函数的时间复杂度：

函数	时间复杂度元
index[i]	O(1)
append	O(1)
pop()	O(1)
pop(i)	O(n)
insert(i,iterm)	O(n)
del	O(n)
reverse	O(n)
sort	O(nlogn)
for循环遍历	O(n)
使用in判断元素是否存在	O(n)
切片取值：list[x,y]	O(k),k等于x到y之间的个数
删除列表切片	O(n)
设置列表切片	O(n+k)
两个列表相加	O(k)，k代表第二个列表中元素的个数
两个列表相乘法	O(nk)

• dict中，常见函数的时间复杂度

函数	时间复杂度元
copy	O(n)
get取值	O(1)
set	O(1)
delete	O(1)
in判断元素是否在字典中	O(1)
for循环遍历	O(n)

线性表

• 编写程序的税后，经常要将一组（通常为某个类型）的数据作为整体来管理和使用，这样就需要创建元素组，使用变量来接收，传进和传出函数等，还可以对元素的个数进行调整（增加或者删除）
• 对于这种需求，最简单的就是将一组数据看作一个序列，用元素在序列中的位置和顺序表示数据之间的某种关系
• 这样一组序列元素的组织形式，就是线性表
• 一个线性表是某类元素的一个集合，还会记录着元素之间的一种顺序关系
• 线性表是最基本的数据结构之一，还经常被用作更复杂的数据结构的实现的基础
• 根据线性表的存储方式，分为两种实现模型：
• • 顺序表：将元素存放在一块连续的存储区域内，元素之间的顺序由他们的存储顺序来表示
• • 链表：将元素存放在通过链接构造起来的一系列存储块当中，每个存储单元的链接指向下一个存储快，可以理解为指针

顺序表

顺序表的连续存储

• 顺序表分为基本顺序表和外置顺序表两种结构
• • 基本顺序表的元素是连续存储的，每个元素占用的存储单元大小股东相同，元素的下表是其逻辑地址
• • 元素的物理地址（实际内存地址）可以通过存储区的其实地址加上逻辑地址（第i个元素）与顿出单元大小的乘积获得
• • 因此，访问股东元素时，不需要从头遍历，通过计算便可获得对应地址及其时间复杂度
• 元素外置顺序表
• • 如果元素的存储单元大小不统一，就需要采用元素外置的顺序表，将实际数据元素另行存储，而顺序表中个单元位置上存储的是对应元素的地址信息（即链接）
• • 由于每个链接所修的存储量相同，那么就可以计算出元素链接的存储位置，然后通过链接就可以找到实际存储数据的物理地址
• • 注意：元素外置的顺序表中，存储的不是数据元素的大小，而是每一个元素的链接地址，这个顶底所占用的内存通常很小

顺序表的两种基本实现方式

• 一个顺序表分为两部分，一部分是表中元素的集合，另外一部分是实现正确操作而记录的信息，这部分信息主要包括数据表的容量和当前已经存入的元素个数
• 顺序表的基本实现方式有两种：
• • 一体式：存储信息的单元和元素存储区以连续的方式安排在一个区域内，两部分整体形成一个完整的顺序表对象（即相邻的内存单元中）
• • 分离式：表对象只保存整个表有关的信息（容量和元素个数）及指向数据元素存储位置的指针或链接，实际元素存放在临沂个独立的元素存储区内，通过放置在表对象中的链接或指针查找
• 存储数据时，当集合的实际存储量大于预估的情况，就需要对元素的存储区进行扩充
• • 一体式结构，由于顺序表信息区与数据区连续存储在一起，因此如果想要扩充，就必须整体搬迁，即整个数据表对象（指存储顺序表的结构信息的区域）改变了
• • 分离式的扩充，可以在不改变对象的前提下，对其数据区域进行扩充， 代码中所有使用这个表的地方必须要修改
• • 只要程序的运行环境（计算机系统）还有空闲的存储，这种表结构就不会因为满了而无法进行
• 因此，为了考虑数据的动态变化，通常会使用分离式存储
• 扩充的两种策略：
• • 每次扩充增加固定树木的存储位置，这种策略叫做线性增常，这种方式节省空间，但是扩充操作频繁，操作次数多
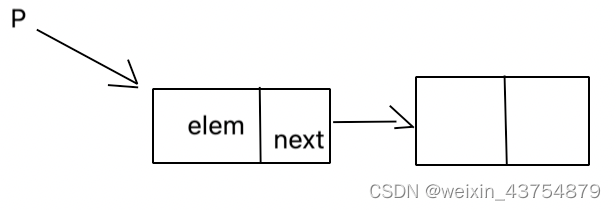
• • 每次扩充量加倍，这种方式减少了扩充操作的执行次数，但是可能会浪费空间资源，以空间换时间，推荐的方式
• 举个例子，list是离散方式的顺序表；str，数值，元祖是一体式的顺序表

链表

• 顺序表的构建需要预先知道数据大小来神器你个连续的存储空间，而在进行扩充时没有需要进行数据的千一，因此这种方式使用起来不是很灵活
• 链表结构，可以充分利用计算机的内存空间，实现领过的内存动态管理
• 链表的定义：是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续的存储，而是在每个节点（数据存储单元）中存放下一个节点的位置信息（即地址）
• 即每一个节点中，都包含当前节点的数据和下一个节点的地址信息

单向链表

• 单项链表也叫单链表，是链表中最简单的一种形式
• 他的每个节点包含两个域，一个是信息域，一个是链接域
• 这个链接指向表中的下一个节点，而最后一个节点的链接域是一个空值
  
• 上图中，elem用来存放具体的数据
• 链接域next，用来存放下一个节点的位置（即python中的标识）
• 变量p指向链表头节点（首节点）的位置，从p出发能找到任意节点
• 一个单链表，如果要实现的话，需要包含以下操作
• • 判断链表是否为空
• • 链表的长度
• • 遍历整个链表
• • 链表头部添加元素
• • 链表尾部添加元素
• • 指定位置添加元素
• • 删除节点
• • 查找某个节点是否存在
• 单链表的代码实现方式如下：

class Node():

    def __init__(self,elem):
        '''定义链表的节点，elem是数据，next是下个节点的指针'''
        self.elem = elem
        self.next = None

class Link_List():

    def __init__(self,node=None):
        '''初始化函数，将节点作为一个整体传入'''
        self._head = node

    def is_empty(self):
        ''' 判断非空'''
        return self._head==None

    def length(self):
        ''' 计算链表长度'''
        ''' 需要一个游标的标识，来记录当前访问到哪个位置上了'''
        cur= self._head # cur初始值指向head，意味着他指向第一个值
        count = 0 # count记录列表中元素的个数
        '''不用cur.next=None作为条件，原因是最后一个元素的指针为None
        如果以他为判断条件，会少计数1'''
        while cur !=None:
            count +=1
            '''cur有next用法的原因：
            cur = self._head = node,node中存在next属性'''
            cur= cur.next
        return count

    def travel(self):
        ''' 遍历整个链表'''
        cur = self._head
        while cur != None:
            print(cur.elem,end=" ")
            cur = cur.next
        print("")

    def add(self,itrem):
        ''' 链表头部添加元素'''
        ''' 最终要达到的效果，新节点的next指向原头部，然后头部节点指向新node'''
        ''' 修改的时候要注意先后顺序，必须先让新节点的next指向原头部
        因为必须根据原头部来确定新节点后需要跟的node，否则会丢节点'''
        node = Node(itrem)# 数据元素封装为链表的节点
        node.next = self._head#新节点的next指向原头部
        self._head=node#头部指向新节点



    def append(self,itrem):
        ''' 链表尾部追加元素'''
        '''先设置新的节点，遍历整个列表之后，将最后一个节点的指针指向新节点'''
        node = Node(itrem)
        '''如果链表是一个空列表，那么node就是None，没有next属性，因此需要考虑特殊情况'''
        if self.is_empty():
            self._head = node
        else:
            cur = self._head
            while cur.next != None:
                cur = cur.next
            cur.next = node

    def insert(self,pos,itrem):
        ''' 链表随意位置插入元素
        :pos 从0开始索引
        '''
        '''插入元素，移动的时候要移动到目标元素的前一个位置
        现将新节点的node指向下一个元素，:再将前一个的指针指向新节点'''
        if pos <=0:#小于0，相当于头部插入
            self.add(itrem)
        elif pos >(self.length()-1):#大于列表总长度，相当于尾部添加
            self.append(itrem)
        else:
            pre = self._head  # 可以理解为插入元素的游标，当前指向第一个节点
            count = 0
            while count < (pos - 1):  # 判断让其指向pos的前一个节点
                count += 1
                pre = pre.next
            # 当循环退出之后，pre指向pos-1
            node = Node(itrem)  # 创建新的node节点
            node.next = pre.next  # pre当前指向的就是要插入的位置，因此先让node指向目标节点
            pre.next = node  # 然后修改pre的指针，指向node


    def remove(self,itrem):
        ''' 删除节点'''
        '''可以使用两个游标节点，前一个和后一个保持一个节点的距离
        删除节点的时候，让前一个节点指向后一个节点所指向的节点'''
        cur = self._head
        pre = None
        while cur!=None:
            if cur.elem == itrem:
                # 元素相等的情况下，需要判断是否是头节点，
                # 因为刚开始pre是None，没有next属性
                if cur == self._head:
                    self._head = cur.next
                else:
                    pre.next  = cur.next
                break
            else:
                pre = cur
                cur = cur.next

    def search_index(self,pos):
        ''' 查找元素'''
        cur = self._head  # 可以理解为插入元素的游标，当前指向第一个节点
        if pos <=0:
            print(cur.elem)
        else:
            count = 0
            while count <=pos :  # 判断让其指向pos的前一个节点
                count += 1
                if count == self.length():
                    break
                cur = cur.next
            print(cur.elem)

    def search_value_1(self, itrem):
        cur = self._head
        count = 0
        while count <(self.length()-1):
            cur = cur.next
            if cur.elem == itrem:
                print(count)
                break
            count +=1
            if count == (self.length()-1):
                print("pass")

    def search_value_2(self, itrem):
        cur = self._head
        while cur !=None:#cur为None，意味着cur已经走到了链表的最后一位
            if cur.elem == itrem:
                return True
            else:
                cur= cur.next
        return False
if __name__ == '__main__':
    ll = Link_List()
    print("是否为空：",ll.is_empty())
    print("长度：",ll.length())
    ll.add(10)
    ll.insert(pos=1,itrem="ppp")
    ll.append(1)
    ll.insert(pos=-1,itrem="fdjfgir")
    print("是否为空：",ll.is_empty())
    print("长度：",ll.length())
    ll.append("i")
    ll.append("love")
    ll.append("lalal")
    ll.append(2)
    ll.append(3)
    ll.insert(pos=7,itrem="hahaha")
    ll.search_index(-1)
    ll.search_value_1("lik")
    print(ll.search_value_2("i"))
    ll.travel()
    ll.remove("fdjfgir")
    ll.travel()
    ll.remove(3)
    ll.travel()
    ll.remove("i")
    ll.travel()
    **************************执行结果***************************
是否为空： True
长度： 0
是否为空： False
长度： 4
fdjfgir
pass
True
fdjfgir 10 ppp 1 i love lalal hahaha 2 3 
10 ppp 1 i love lalal hahaha 2 3 
10 ppp 1 i love lalal hahaha 2 
10 ppp 1 love lalal hahaha 2 

顺序表和单链表的对比

• 链表失去了顺序表堆积读取的优点，同时链表由于增加了节点的指针，空间开销较大，单对存储空间的使用要相对灵活
• 链表和顺序表的各种操作复杂度如下：

操作	链表	顺序表
访问元素	O(n)	O(1)
在头部插入/删除	O(1)	O(n)
在尾部插入/删除	O(n)	O(1)
在中间插入/删除	O(n)	O(n)

• 虽然表面看起来是时间复杂度都是O(n)，但是链表和顺序表插入和删除时是完全不同的操作
• • 链表耗时是遍历查找，删除和插入操作本身的时间复杂度是O（1）
• • 顺序表查找很快，主要好事的操作是拷贝和覆盖
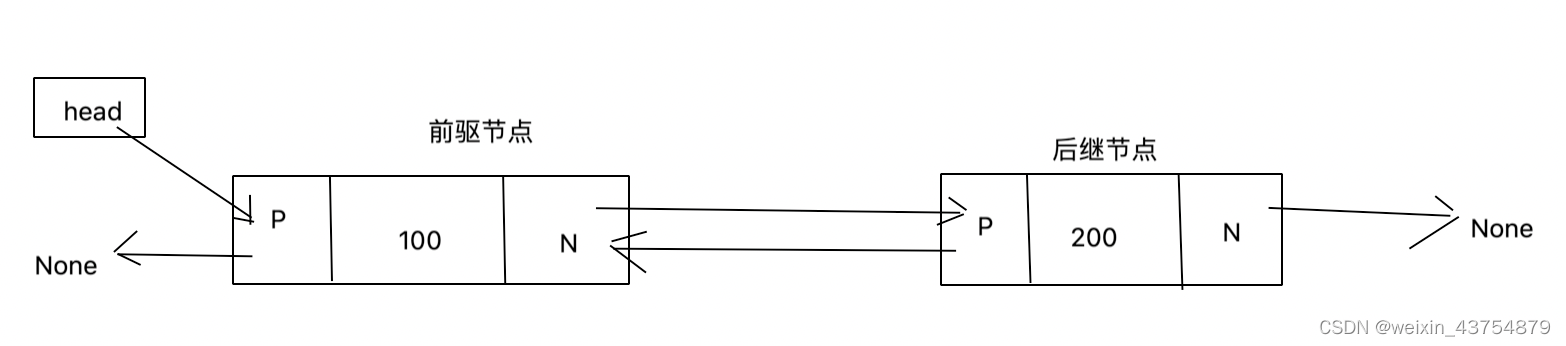
• • 因为除了目标元素在尾部的特殊情况，顺序表进行插入和删除时，需要对操作点之后的所有元素今夕你个前后移位的动作，只能通过拷贝和覆盖的方式进行

双向链表

• 比单向链表更复杂的结构，每个节点有两个链接，一个指向前一个节点，当次节点为第一个节点时，指向空值，而另外一个指向下一个节点，当次节点为最后一个节点时，指向空值
  
• 双向链表应实现的操作有：
• • 链表是否为空
• • 链表长度
• • 遍历链表
• • 链表头部添加
• • 链表尾部添加
• • 指定位置添加
• • 删除节点
• • 查找节点是否存在
• 代码如下：

class Node():

    def __init__(self,iterm):
        '''
        :param iterm: 传入节点的数据
        '''
        self.elem= iterm
        self.next = None#后继指向
        self.prev = None#前驱指向

class DoubleLinkList():
    '''双链表操作'''
    def __init__(self,node = None):
        '''
        双链表初始化函数，链表头指向节点
        :param node: 第一个节点
        '''
        self.__head = node

    def is_empty(self):
        ''' 判断是否为空'''
        return self.__head is None

    def length(self):
        '''求长度'''
        # cur为游标，指向移动的游标，遍历节点
        cur = self.__head
        #count 计算节点数量
        count = 0
        #遍历节点
        while cur != None:
            count +=1
            cur = cur.next # 游标指向下一个节点
        return count

    def travel(self):
        ''' 遍历链表'''
        cur = self.__head
        while cur != None:
            print(cur.elem,end = " ")
            cur = cur.next # 游标指向下一个节点
        print("")

    def add(self,iterm):
        '''
        直接在首节点插入元素，插入时，先将插入节点的N指向原首节点的P
        再将头部指向插入节点的P，最后将原首节点的P指向插入节点的N
        :param iterm: 要插入的元素
        '''
        #方法一，先将插入node的后继指向原节点的前驱
        flag = False # 定义一个标志，用于区分是否是空列表
        node = Node(iterm)  # 数据元素封装为链表的节点
        # 在这里判断的原因是，放在下面，新节点已添加，无法判断链表是否为空
        if self.is_empty():
            flag = True
        node.next = self.__head  # 新节点的next指向原头部
        self.__head  = node  # 头部指向新节点
        if flag == False :# 如果标志不是True，说明链表不为空，就需要执行下面的操作
            node.next.prev = node#将原首节点的前驱指向插入节点的后继

    def append(self,iterm):
        '''
        尾部追加元素
        :param iterm:
        :return:
        '''
        '''先设置新的节点，遍历整个列表之后，将最后一个节点的指针指向新节点'''
        node = Node(iterm)
        '''如果链表是一个空列表，那么node就是None，没有next属性，因此需要考虑特殊情况'''
        if self.is_empty():
            self.__head = node
        else:
            cur = self.__head
            while cur.next != None:
                cur = cur.next
            cur.next = node# 追加时将最后一个节点的后继指向新节点的前驱
            node.prev = cur# 再将新节点的前驱指向最后一个节点的后继

    def insert(self,pos,iterm):
        '''
        随机插入元素
        :param pos: 插入位置
        :param iterm: 插入的元素
        '''
        if pos <=0:#小于0，相当于头部插入
            self.add(iterm)
        elif pos >(self.length()-1):#大于列表总长度，相当于尾部添加
            self.append(iterm)
        else:
            pre = self.__head  # 可以理解为插入元素的游标，当前指向第一个节点
            count = 0
            while count <= (pos - 1):  # 判断让其指向pos的前一个节点
                count += 1
                pre = pre.next
            # 当循环退出之后，pre指向pos-1
            node = Node(iterm)  # 创建新的node节点
            node.next = pre
            # pre当前指向的就是要插入的位置，因此先让node的后继指向找到的目标节点
            node.prev = pre.prev# node的前驱指向前一个节点( pre.prev为前一个节点)
            pre.prev.next = node#前一个节点的后继指向node
            pre.prev = node#后一个节点的前驱指向node

    def remove(self,itrem):
        '''
        删除元素为elem的节点
        :param itrem: 元素信息
        '''
        cur = self.__head
        while cur != None:
            if cur.elem == itrem:
                # 元素相等的情况下，需要判断是否是头节点，
                # 因为刚开始pre是None，没有next属性
                if cur == self.__head:
                    self._head = cur.next
                    if cur.next !=None:#判断链表是否只有一个节点，是的话就不需要指向了
                        cur.next.prev = None
                else:
                    cur.prev.next = cur.next # 要删除节点的前一个节点的后继指向下一个节点
                    if cur.next !=None:
                        cur.next.prev = cur.prev# 要删除节点的后一个节点的前驱指向前一个节点
                break
            else:
                cur = cur.next

    def search(self,iterm):
        cur = self.__head
        while cur != None:  # cur为None，意味着cur已经走到了链表的最后一位
            if cur.elem == iterm:
                return True
            else:
                cur = cur.next
        return False


if __name__ == '__main__':
    ll = DoubleLinkList()
    print("是否为空：", ll.is_empty())
    print("长度：", ll.length())
    ll.add(10)
    ll.append(100)
    ll.add(20)
    ll.travel()
    ll.insert(1,"haha")
    ll.travel()
    ll.remove(100)
    ll.travel()
    print(ll.search(10))
    ***********************run——result*****************
是否为空： True
长度： 0
20 10 100 
20 haha 10 100 
20 haha 10 
True

单向循环链表

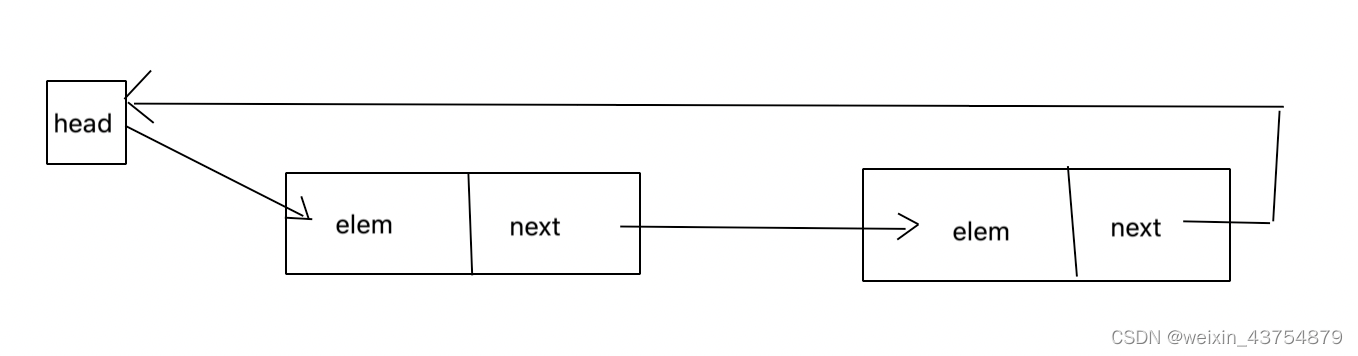
• 单向循环链表是单链表的一个变形，脸比啊中最后一个节点的next不在乎为None，而是指向脸憋哦的头节点
  
• 单项循环链表的操作有：
• • 链表是否为空
• • 链表长度
• • 遍历链表
• • 链表头部添加
• • 链表尾部添加
• • 指定位置添加
• • 删除节点
• • 查找节点是否存在
• 代码如下：

在这里插入代码片class Node():

    def __init__(self,iterm):
        '''
        :param iterm: 传入节点的数据
        '''
        self.elem= iterm
        self.next = None#后继指向

class ForLinkList():
    '''单向循环操作'''
    def __init__(self,node = None):
        '''
        单向循环链表表初始化函数，节点的next指向下一个节点
        最后一个节点的next区域指向头节点
        如果链表只有一个节点，就是节点的next区域指向自己
        :param node: 节点
        '''
        self.__head = node
        if node:
            node.next = node# node存在，需要设置他的next区域指向他本身
            #可以理解为链表中只有这一个节点

    def is_empty(self):
        ''' 判断是否为空'''
        return self.__head is None

    def length(self):
        '''求长度'''
        # cur为游标，指向移动的游标，遍历节点
        cur = self.__head# 创建指针
        #count 计算节点数量
        if self.is_empty():
            return 0  # 空链表，直接返回0
        count = 1 #count必须从1开始，因为节点的next等于头节点时，没有进入循环，count没有+1
        #遍历节点
        while cur.next != self.__head:
        # 这里不能使用cur，只能使用cur.next的原因是：创建游标的时候，就使用了cur等于头节点
        # 详见length创建指针的代码
            count +=1
            cur = cur.next # 游标指向下一个节点§
        return count

    def travel(self):
        ''' 遍历链表'''
        cur = self.__head
        if self.is_empty():# 为空，直接但会None，因为空链表进不去循环
            return None
        while cur.next != self.__head:
            print(cur.elem,end = " ")
            cur = cur.next # 游标指向下一个节点
        print(cur.elem,end=" ")# 退出循环的时候，需要再打印当前节点的值，
        # 因为最后一个节点的next，等于头节点，无法进入循环，因此无法打印
        print("")

    def add(self,iterm):
        '''
        链表头部添加元素
        最终要达到的效果，新节点的next指向原头部，然后头部节点指向新node
        最后将尾节点的next指向头节点，需要遍历找到尾节点
        :param iterm: 要插入的元素
        '''
        node = Node(iterm)  # 数据元素封装为链表的节点
        if self.is_empty():
            self.__head=node
            node.next = node
        cur = self.__head
        while cur.next!=self.__head:
            cur = cur.next
        node.next = self.__head  # 新节点的next指向原头部
        self.__head = node  # 头部指向新节点
        cur.next = self.__head


    def append(self,iterm):
        '''
        尾部追加元素
        :param iterm:
        :return:
        '''
        '''先设置新的节点，遍历整个列表之后，将最后一个节点的指针指向新节点'''
        node = Node(iterm)
        '''如果链表是一个空列表，那么node就是None，没有next属性，因此需要考虑特殊情况'''
        if self.is_empty():
            self.__head = node
            node.next = node
        else:
            cur = self.__head
            while cur.next != self.__head:
                cur = cur.next
            node.next = self.__head  # 先将新节点的next指向头节点
            cur.next = node# 再最后一个节点next指向node


    def insert(self,pos,iterm):
        '''
        随机插入元素
        :param pos: 插入位置
        :param iterm: 插入的元素
        '''
        if pos <=0:#小于0，相当于头部插入
            self.add(iterm)
        elif pos >(self.length()-1):#大于列表总长度，相当于尾部添加
            self.append(iterm)
        else:
            pre = self.__head  # 可以理解为插入元素的游标，当前指向第一个节点
            count = 0
            while count < (pos - 1):  # 判断让其指向pos的前一个节点
                count += 1
                pre = pre.next
            # 当循环退出之后，pre指向pos-1
            node = Node(iterm)  # 创建新的node节点
            node.next = pre.next  # pre当前指向的就是要插入的位置，因此先让node指向目标节点
            pre.next = node  # 然后修改pre的指针，指向node

           def remove(self,itrem):
        '''
        删除元素为elem的节点
        可以使用两个游标节点，前一个和后一个保持一个节点的距离
        删除节点的时候，让前一个节点指向后一个节点所指向的节点
        :param itrem: 元素信息
        '''
        cur = self.__head
        if self.is_empty():
            return
        pre = None
        while cur.next != self.__head:
            if cur.elem == itrem:
                # 元素相等的情况下，需要判断是否是头节点，
                # 因为刚开始pre是None，没有next属性
                if cur == self.__head:#头节点
                    # 如果删除的是头节点，需要遍历找到尾节点，修改尾节点的next指向
                    wei = self.__head
                    while wei.next != self.__head:
                        wei = wei.next
                    #跳出节点时，wei指向最后一个节点
                    self.__head = cur.next
                    wei.next = self.__head
                else:#中间节点
                    pre.next = cur.next
                return # 这里代表整个头节点的结束，使用return退出整个函数
            # 如果使用break，标识退出函数中的循环，下面的代码还会继续执行
            else:
                pre = cur
                cur = cur.next
        #因为cur为尾节点的时候不进入循环，因此跳出循环体，cur才指向尾节点
        if cur.elem == itrem :
            if cur ==self.__head:
                self.__head =None
            else:
                pre.next = cur.next

    def search(self,iterm):
        cur = self.__head # 如果是空列表，下面就无法去判断.next,因粗需要判断是否为空
        if self.is_empty():
            return False
        while cur.next != self.__head:  # cur为None，意味着cur已经走到了链表的最后一位
            if cur.elem == iterm:
                return True
            else:
                cur = cur.next
        if cur.elem == iterm:#因为最后一个节点未进入循环，因此没有进行比较，需要重新判断
            return True
        return False


if __name__ == '__main__':
    ll = ForLinkList()
    print("是否为空：", ll.is_empty())
    print("长度：", ll.length())
    ll.add(20)
    ll.append(100)
    ll.travel()
    ll.add(10)
    ll.travel()
    ll.insert(1,"haha")
    ll.travel()
    ll.remove(100)
    ll.travel()
    ll.remove(10)
    ll.travel()
    ll.remove(20)
    ll.travel()
    ll.remove("haha")
    print(ll.search(10))
    *************run_result****************
是否为空： True
长度： 0
20 100 
10 20 100 
10 haha 20 100 
10 haha 20 
haha 20 
haha 
False