1. 异或门与半加器

异或门就是实现一个最简单的整数加法所需要使用的基本门电路。

当输入两位都是 11 的时候，还需要向更左侧的一位进行进位。这个就对应一个与门，也就是当加数和被加数都是 1 的时候，进位才会是 1.

所以一个异或门算出个位，通过一个与门计算出是否进位，我们就通过电路算出了一个一位数的加法。

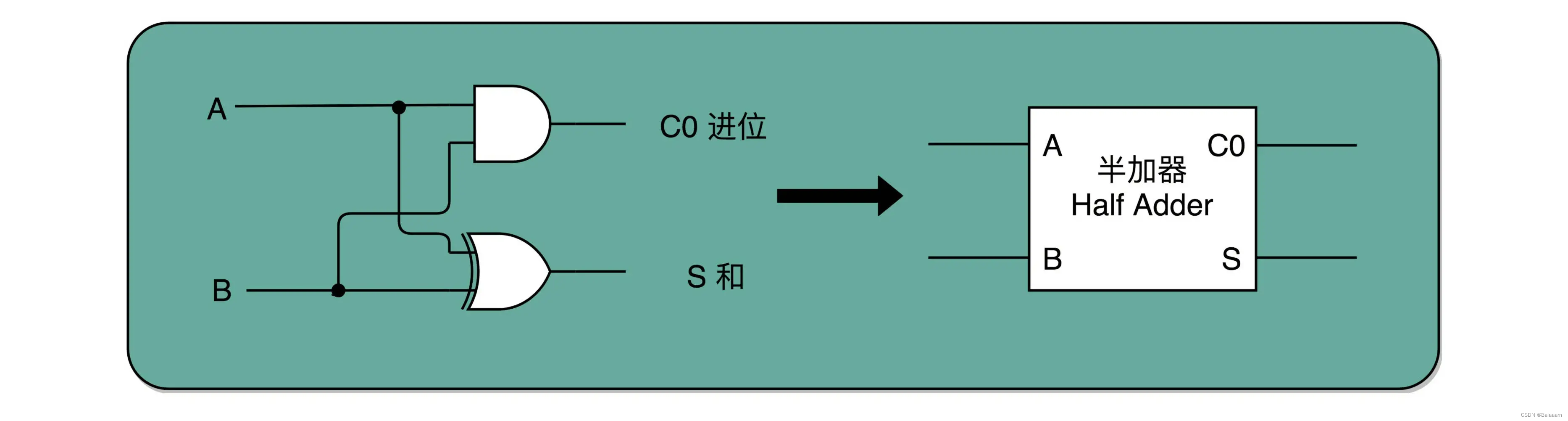
于是我们将两个门电路打包，给它去一个名字，叫作 半加器（Half Adder）。

2. 全加器

半加器可以解决个位的加法问题，但是对于二位数，就不行了。两位用一个半加器之所以不能完成计算，是因为二位除了一个加数和被加数之外，还需要加上来自个位的进位信号，一个需要三个数进行相加，才能得到结果。

全加器就可以解决这个问题。我们用两个半加器和一个或门，就能组成一个全加器。

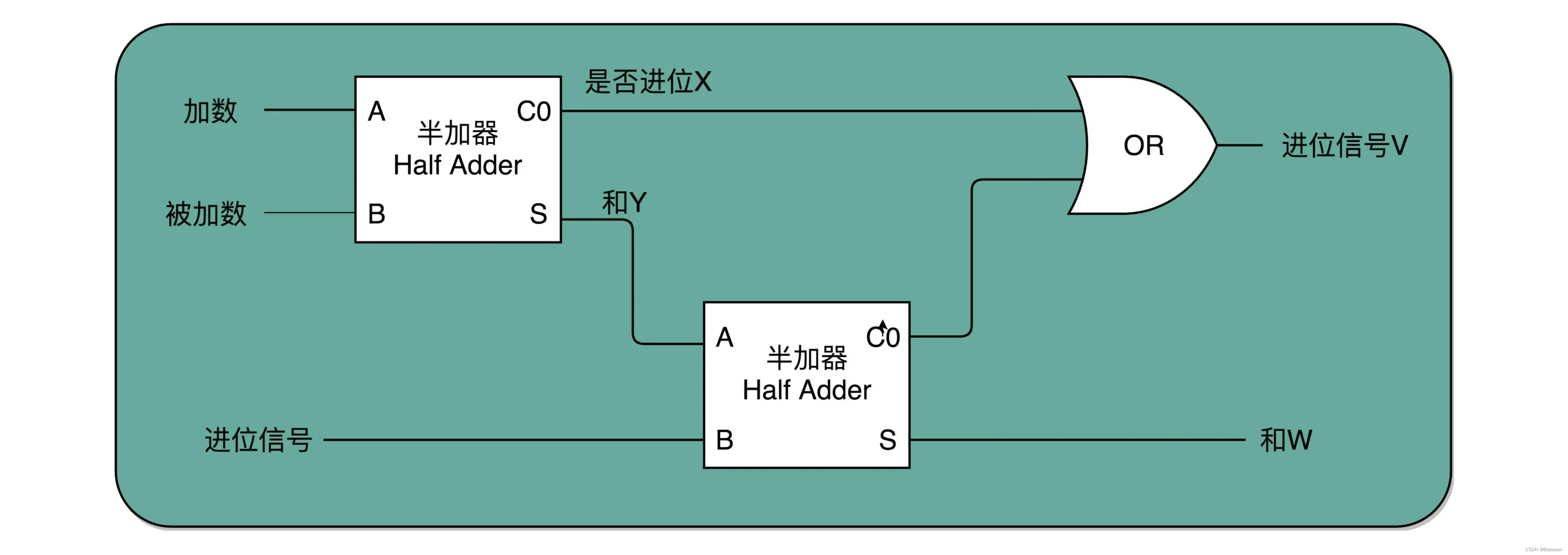
第一个半加器，用和个位的加法一样的方式，得到是否进位 X 和对应的二个数加和后的结果 Y，这样两个输出。然后，把这个加和后的结果 Y，和个位数相加后输出的进位信息 U，再连接到一个半加器上，就会再拿到一个是否进位的信号 V 和对应的加和后的结果 。W 就是在第二位的结果。把两个半加器的进位输出，用一个或门的输入连接起来，只要两次加法中任何一次需要进位，那么在第二位上，就会向左侧进一位。

我们将 8 个全加器串联起来，就实现了一个进行对应两个 8 bit 数的加法。16、32、64位依此类推。

唯一需要注意的是，对于这个全加器，在个位，我们只需要用一个半加器，或者让全加器的进位输入始终是 0。因为个位没有来自更右侧的进位。而最左侧的一位输出的进位信号，表示的并不是再进一位，而是表示加法是否溢出了。

3. 总结

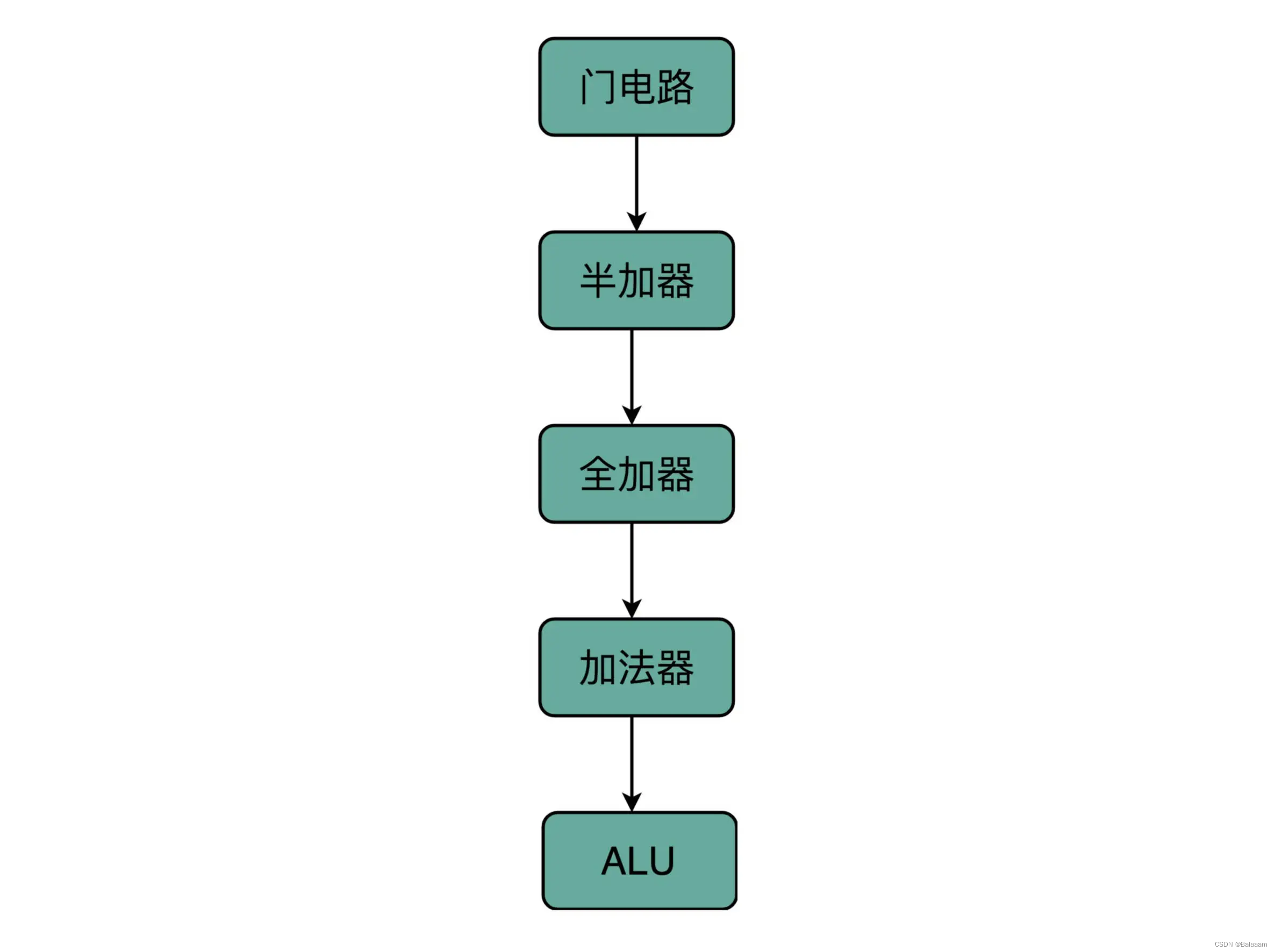
在硬件层面，通过门电路、半加器、全加器一层层搭出了加法器这样的功能组件。我们把这些用来做算术逻辑计算的组件叫作 ALU，也就是算术逻辑单元。当进一步打造强大的 CPU 时，我们不会再去关注最细颗粒的门电路，只需要把门电路组合而成的 ALU，当成一个能够完成基础计算的黑盒子就可以了。

这其实就是计算机中，无论软件还是硬件中一个很重要的设计思想，分层。

参考

极客时间《深入浅出计算机组成原理》：http://gk.link/a/11UMi