前言

前面我们学习的都是一些线性的数据结构，比顺序表，链表，栈和队列，逻辑结构比较简单，今天我们重点学习的是一种非线性的数据结构，就是树形结构。

一、树

在现实生活中我们都看到过树，如下图，所以对树的形状会有一个基本的认知

但是在数据结构这门课中我们学习的树可就不是长上面这个样子了，而是下面这个奇怪的样子：

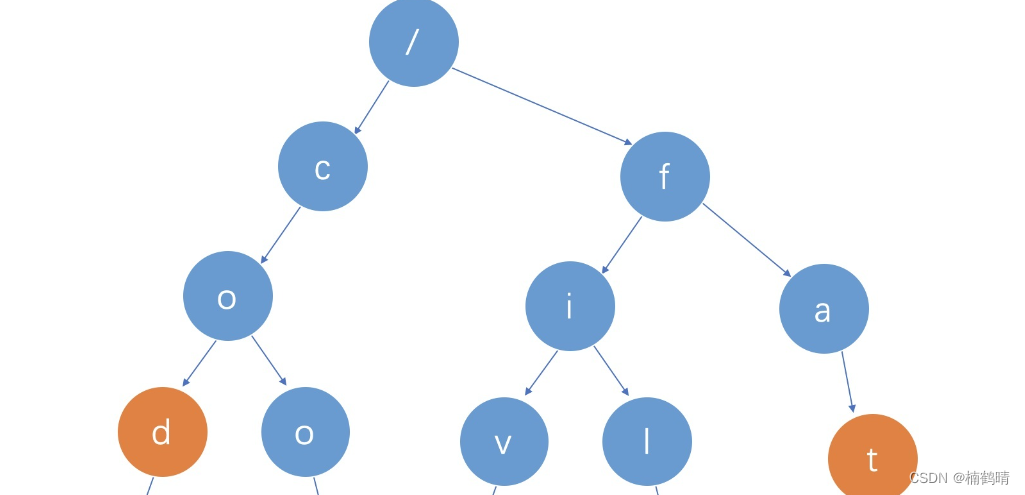
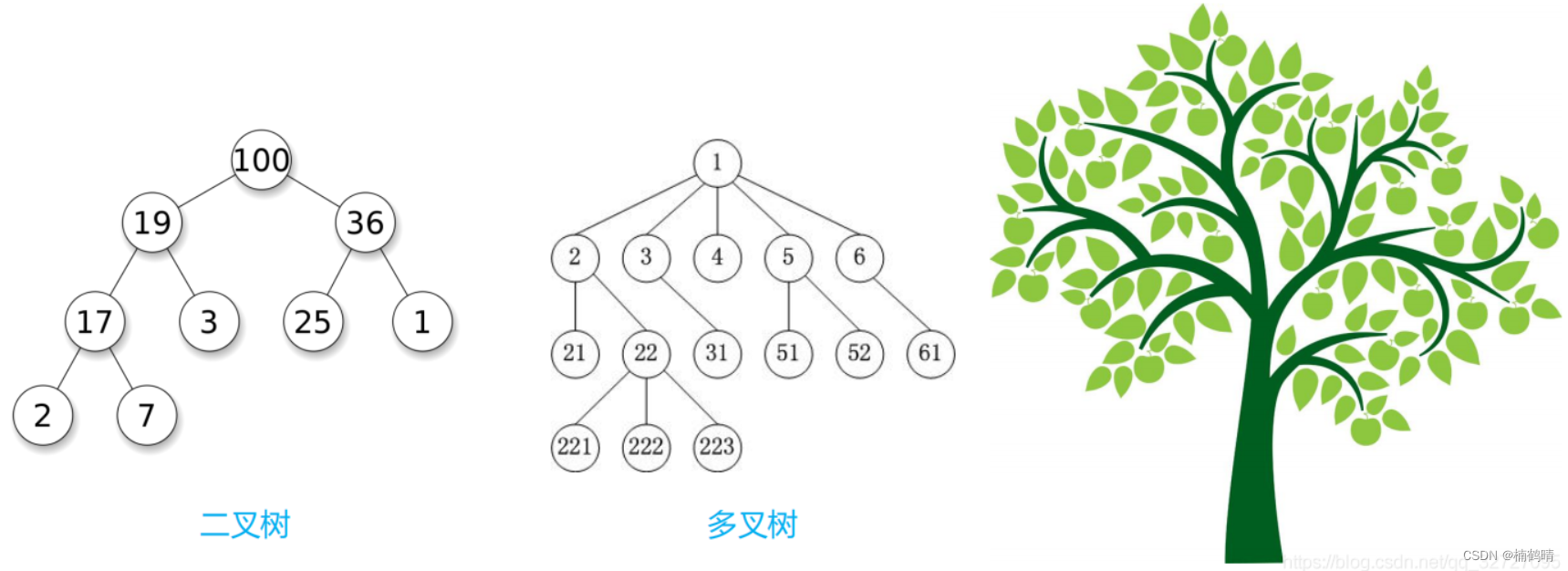
1、树的相关概念

（1）结点

每一个树都是由一个个小小的单元组成，在数据结构中，我们将这样的小单元称为结点。

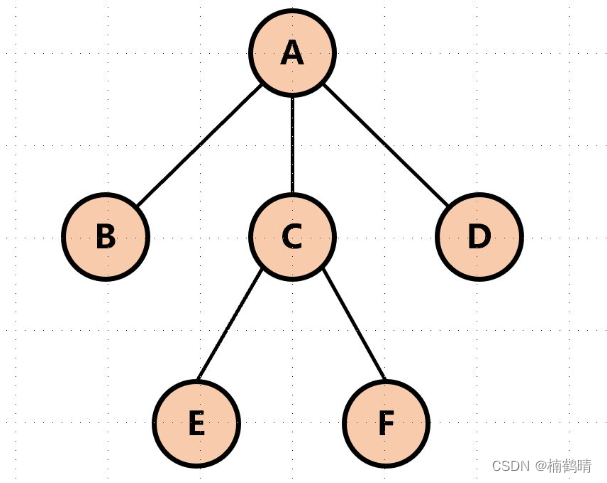
像上面ABCDEF都是这棵树的结点。

（2）结点的度

每一个结点都是相当于一棵子树的根，而根又会有很多的分支，在数据结构中，一个结点有多少个分支，我们就说这个结点的度为多少。比如：

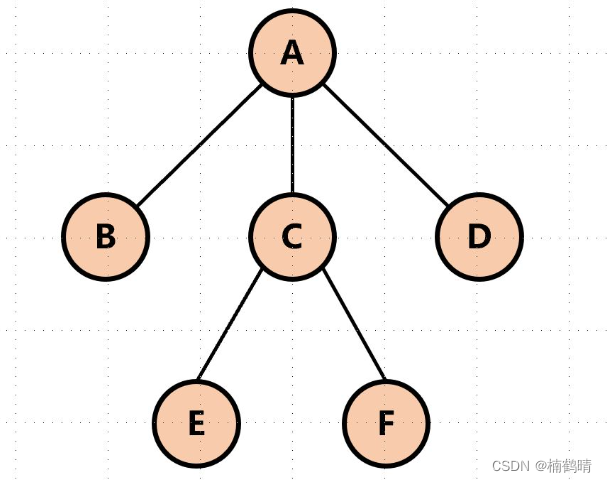
像上面这个图中，A这个结点有三个分支，就说明A的度为3。E和F这两个结点没有分支，我们就说这两个结点的度为0。

（3）叶结点

我们将度为0的结点称为叶子结点，或简称为叶节点。如下图中的EF结点度为0，所以它们为叶节点。

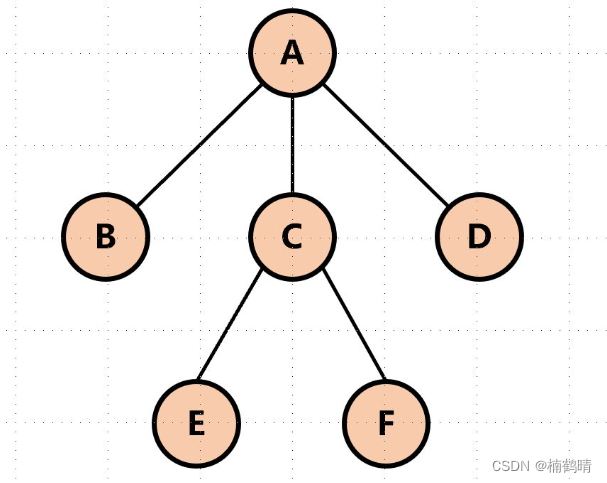
（4）分支结点

与叶子结点相反，度不为0的结点我们称为分支结点，如下图中AC结点的度不为0，所以AC结点为分支结点。

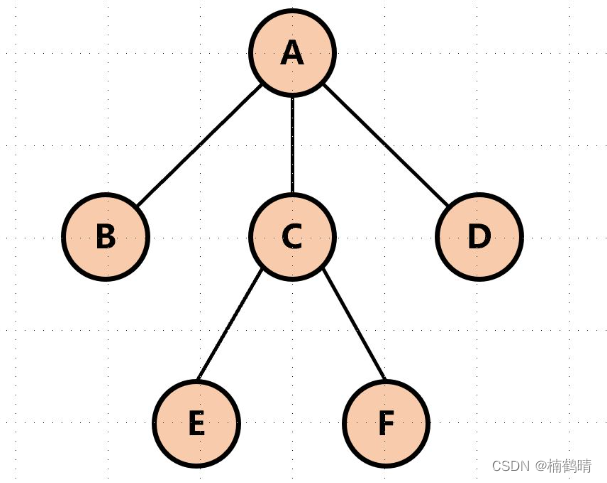
（5）父亲结点

如果一个结点含有分支，也就是包含子树，则我们将这个结点称为其子树的父亲结点或双亲结点，后面我们是用parent来表示。如下图中的A结点有三个分支BCD结点，所以我们成A结点是BCD结点的父亲结点。

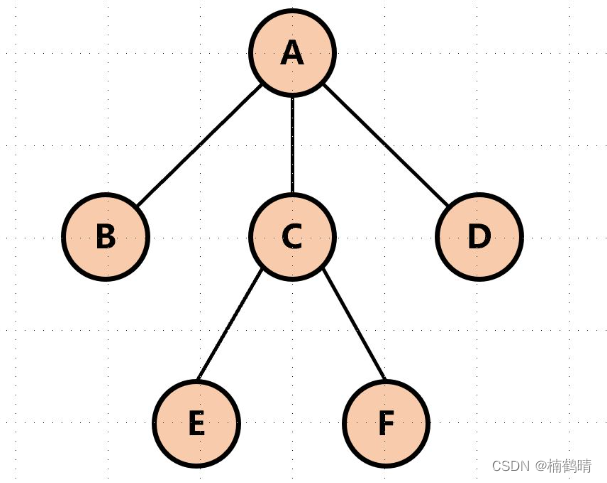
（6）子节点

一个结点含有的子树的根结点我们称为这个结点的子节点，就是我们要知道一个子树是由自己的根节点和另外的子树构成的。下图中：A包含BCD三个子树，BCD三个结点分别为对应子树的根节点，所以我们成BCD结点为A结点的子节点，后面我们是用child来表示。

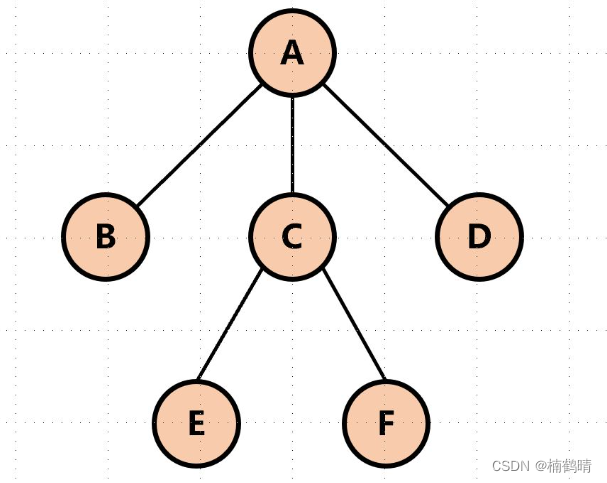
（7）树的度

一棵树中所有结点中度最大的结点的度我们称为这棵树的度，下图中：显然A结点的度最大，是3，所以我们说这棵树的度为3。

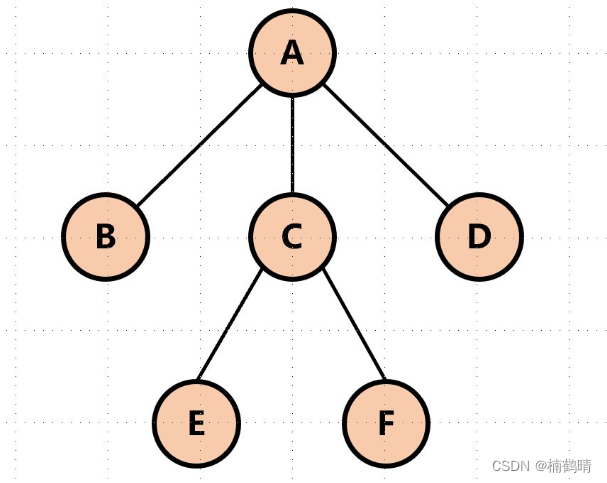
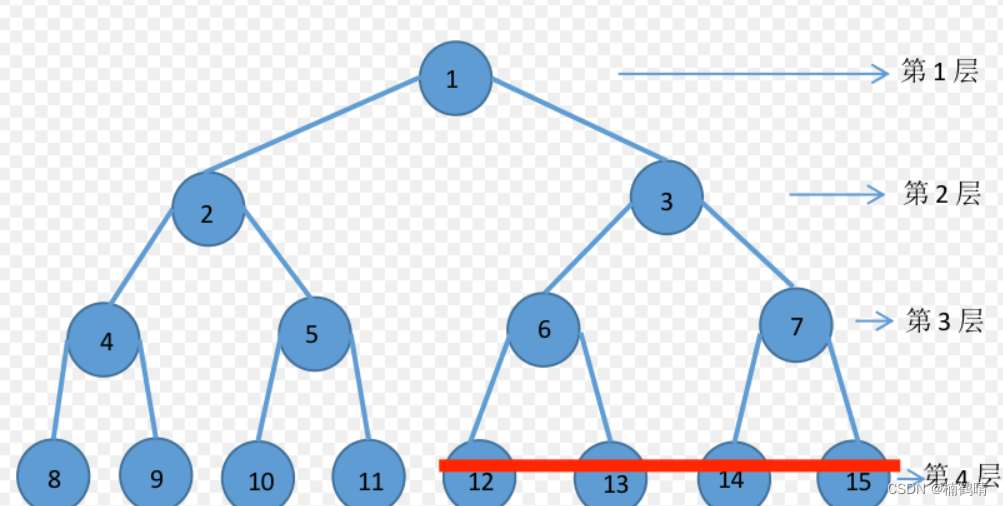
（8）结点的层次

从这棵树的根节点开始定义，我们说根结点是第一层，其子树的根节点为第三层，以此类推。下图中：A为第一层，BCD为第二层，EF为第三层。

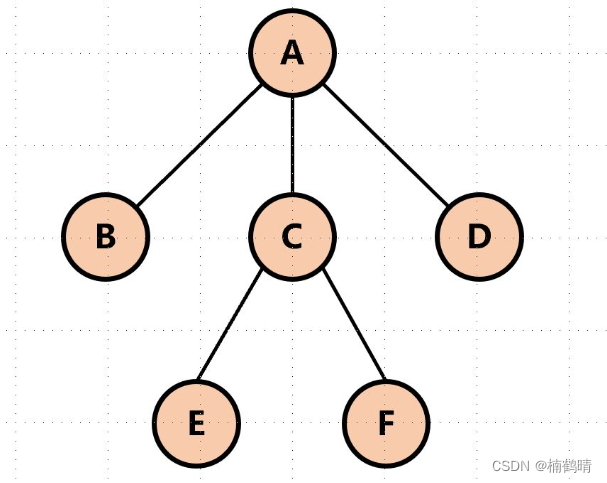
（9）树的深度（高度）

一棵树最大的层次就是这棵树的深度（高度），如下图中：这棵树的最大层次为3，所以我们说这棵树的深度（高度）为3。

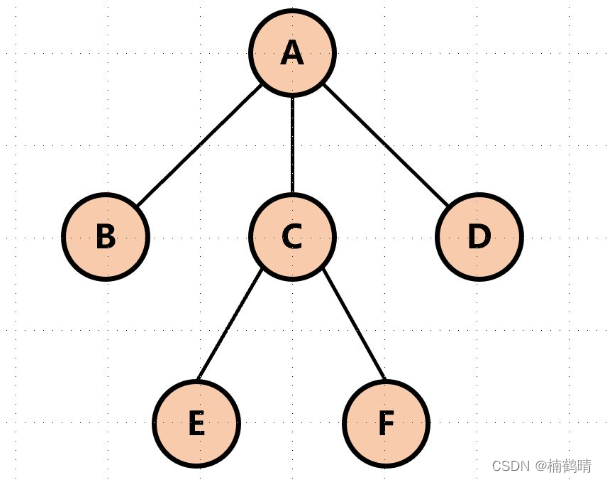
（10）结点的祖先

从根到该节点所经分支上的所有结点都称为该节点的祖先，注：在OJ题中一个结点也可以算成其自己的祖先。如下图中：从A到E，经历了ACE，所以我们成ACE结点都是E结点的祖先。

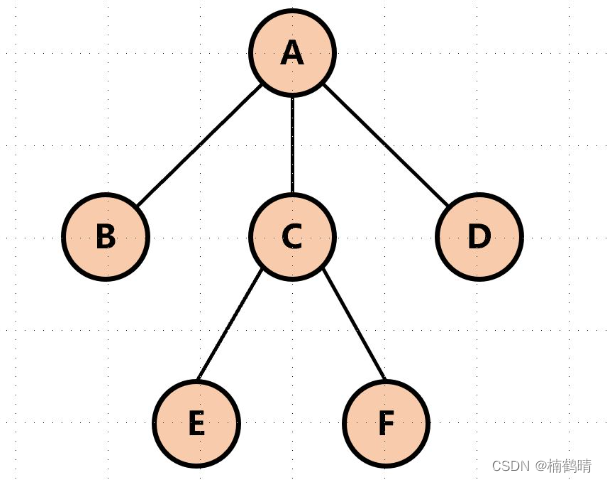
（11）子树

任意一个结点都可以说是由根节点和其自己的子树组成

2、树的表示方法

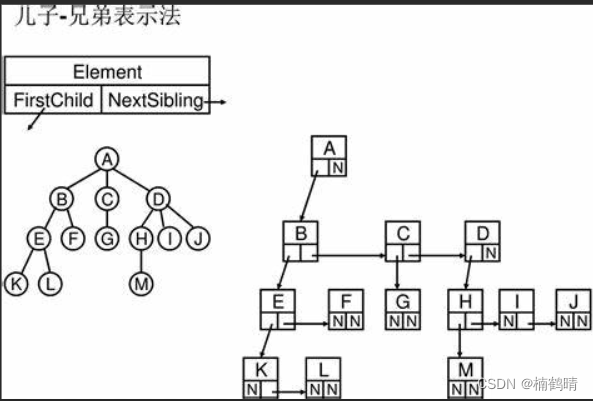
上面介绍的树是树中的一种特殊的结构，二叉树，二叉树中每个节点的度最大为2，但是树就不一样了，树中的每一个结点的度是不确定的，可多可少。所以表示起来会比较麻烦，在这里我们学习一种比较优秀的表示方法：孩子兄弟表示法，这个方法需要和前面学习的链表结合起来，首先需要定义树中结点的结构

// 定义树存储的数据类型
typedef int TreeDataType;

// 定义一棵树的结点的结构
struct TreeNode
{
	TreeDataType data;
	struct TreeNode* first_child;
	struct TreeNode* next_brother;
};

其中data表示结点存储的值，first_child指向的是该节点的第一个孩子，next_brother指向的是该节点向右的下一个结点，我们称为兄弟结点。如下图：

二、二叉树

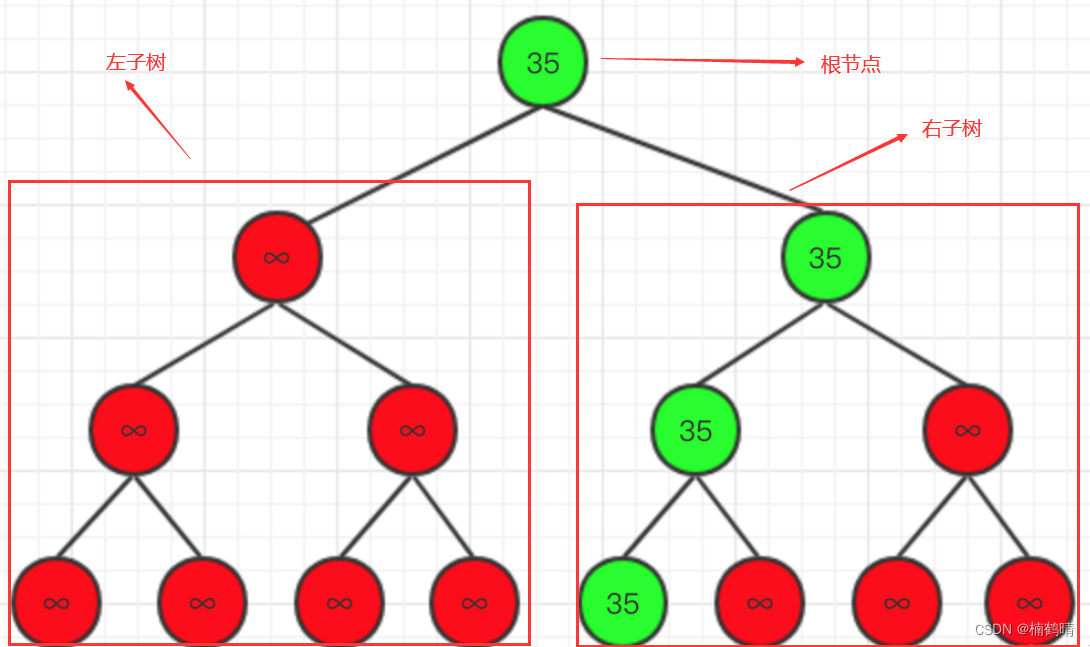
一棵树中，如果每一个结点的度都不超过2，则称这棵树为二叉树。二叉树中的孩子结点是有左右之分的，位于左边的结点称为左孩子结点，位于右边的结点称为右孩子结点，子树同样也有左右之分，位于左边的称为左子树，位于右边的称为右子树。

1、特殊的二叉树

（1）满二叉树

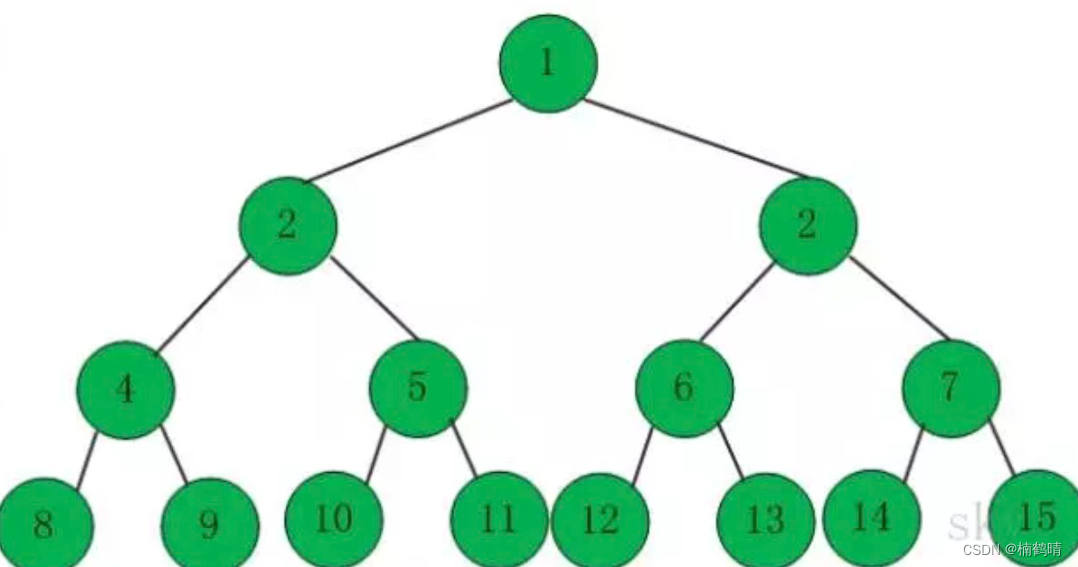
如果每一层的结点都达到最大值，则我们称这棵树为满二叉树，如：一棵树中，第一层是根节点，最多只有一个结点，第二层最大有两个结点，第三层最多有四个结点，第四层最多有8个结点，以此类推，第N层最多有2^(N-1)个结点，如下图就是一棵满二叉树。

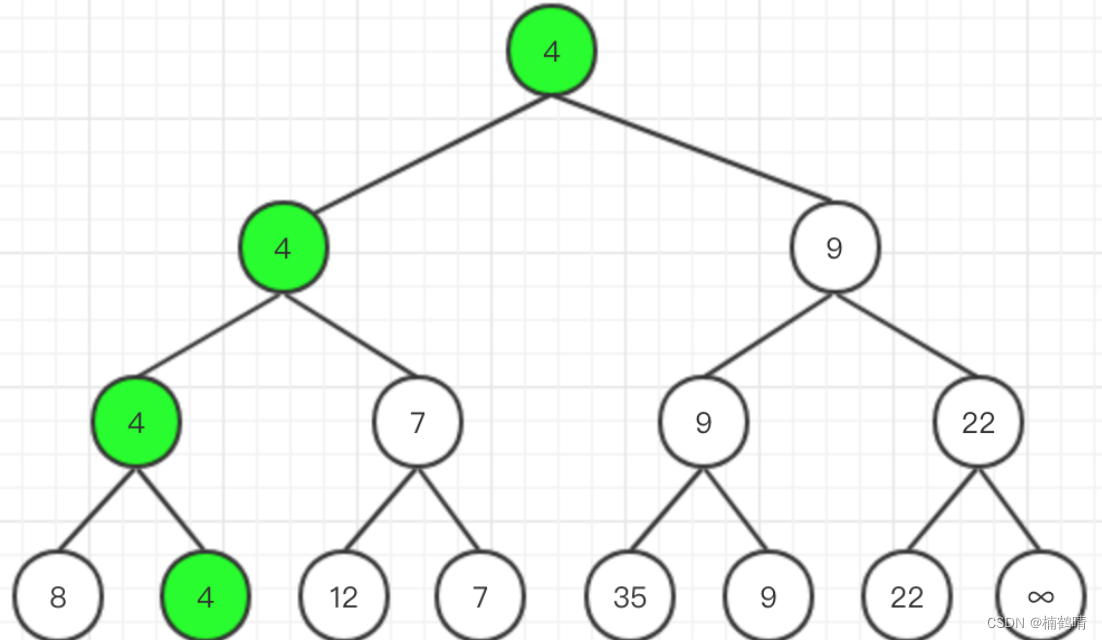
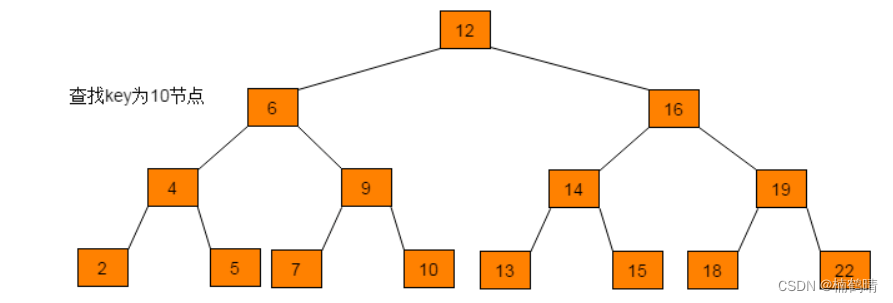
（2）完全二叉树

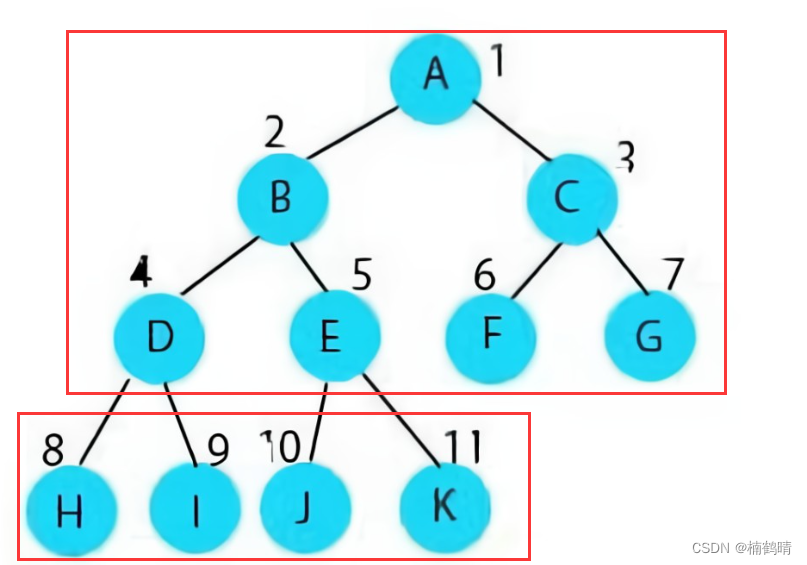
满二叉树是一种特殊的完全二叉树，完全二叉树的特点是：如果这棵树有N层，前N-1层的结点树都是达到对应层的最大值，最后一层可能达到最大，也可能未达到最大，但是从左到右是满的

三、二叉树的一些重要性质

1. 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个结点，如果这棵树是满二叉树，那么此时每一层的结点的数量都会满足以上的性质
2. 若规定根节点的层数为1，则深度为h的二叉树的最大结点树为2^h -1，如果这个树是满二叉树，那么此时这个数的结点数就是达到最大值，为2^h -1，这个结论是根据等比数列的求和公式计算得出的
3. 对于任何的一棵二叉树，如果度为0的结点的个数为n0，度为2的结点个数为n2，那么此时会满足：n0 = n2+1，通常情况下，要注意题目是否给出一个条件是完全二叉树，如果题目说这棵树是一棵完全二叉树，那么此时可以知道，树中度为1的结点个数可能为0或者1，当树中存在的根节点只存在左子树时，那么这种情况下，度为1的结点数为1，当树中不存在这样的子树时，也就是树中的每一个子树都是同时存在左右子树的，那么此时树中度为1的结点数为0。
4. 若规定根节点的层数为1，具有n个结点的满二叉树的深度为h = log2(n+1)，这个结论是由第2个性质推出来的
5. 对于具有n个结点的完全二叉树，如果按照从上至下从左到右的数组顺序对所有结点从0开始编号，则对序号为i的结点有：

• 若i>0,i位置的结点存在双亲结点，序号为：(i-1)/2,若i = 0,则说明此时该节点为该树的根节点，不存在双亲结点
• 若2*i+1<n,则说明该结点存在左子树，左子树的根节点序号为：2*i+1，2*i+1>=n,则说明该结点不存在左子树
• 若2*i+2<n,则说明该结点存在右子树，右子树的根节点序号为：2*i+2，2*i+2>=n,则说明该结点不存在右子树

四、二叉树的一些常见题目

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
   A 不存在这样的二叉树
   B 200
   C 198
   D 199

解：根据二叉树的性质，度为0的结点数比度为2的结点数多1可得答案。

2.下列数据结构中，不适合采用顺序存储结构的是（ ）
A 非完全二叉树
B 堆
C 队列
D 栈

解：非完全二叉树由于其中可能存在只有右子树的情况，所以如果将非完全二叉树中的结点存在于数组中，那么就可能出现内存空间浪费的现象，因此，非完全二叉树不适合顺序存储。堆的本质就是完全二叉树，其中的结点适合存在数组中按下标进行编号，不会出现空间浪费。队列和栈在前面学习过，都是经典的线性结构，适合存在于数组中。

3.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2

解：假设树中叶子结点的个数为x，则度为2的结点个数为x-1，要注意题目中的一个隐含的条件，就是完全二叉树，这个条件告诉我们，树中度为1的结点的数量可能为1或者0，所以我们需要进行分类讨论：
当树中的度为1的结点数为1时：x + x-1 +1 = 2n,即2x = 2n,x = n,此时叶子结点的个数为n
当树中的度为1的结点数为1时：x + x-1 = 2n,即2x = 2n+1,x = n+1/2,显然不符合条件 综上，叶子结点的个数为n

4.一棵完全二叉树的节点数位531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12

解：这道题告诉了我们树的总结点数，所以我们需要想性质，二叉树的最大结点数量为：2^h -1,假设该树的深度为10，则最大结点数位：2^10 -1，就是1023，当该树的深度为9时，最大结点数为：511<523，显然不符合题意，所以该树的深度为10，前9层是满的，最后一层不满

。
5.一个具有767个节点的完全二叉树，其叶子节点个数为（）
A 383
B 384
C 385
D 386

解：解法与第3题一样