在这篇paper中，作者提出了Homi 算法，在运行时通过修剪掉不必要（unpromising）的状态来增强符号执行工具。

1.引言

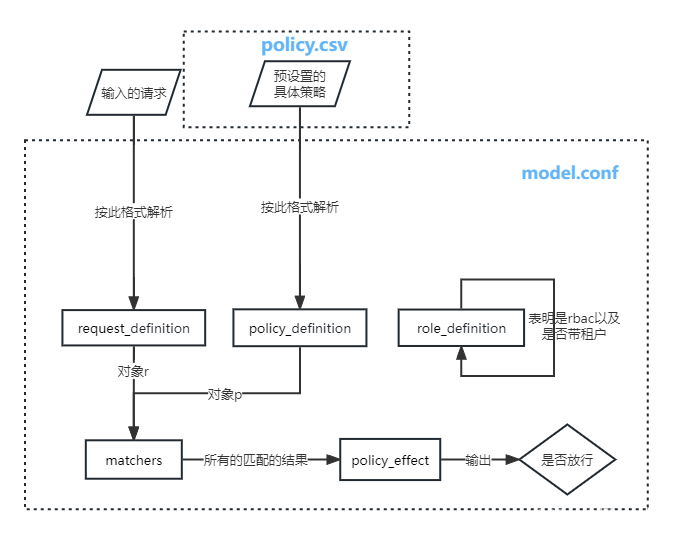
下图是符号执行算法的形式化描述，红框为作者添加的部分：

• 每个状态可以用3元组 $(instr,store,\Phi )$ 描述：

  • $instr$ 为将要执行的指令。

  • $store$ 为将程序变量映射为符号值的map。

  • $\Phi$ 为当前状态对应的路径条件。

• 每个测试用例用2元组 $(\Phi ,Model(\Phi ))$ 描述，$Model(\Phi )$ 为对应输入。

在这篇paper中，作者认为有意义（promising）的状态是那些可以提高分支覆盖率的状态，因此需要修剪掉不必要的状态。那么需要解决的问题有：

• 如何衡量每个状态的重要程度？计算状态分数

• 要修剪掉多少状态? 计算修剪得数量

2.Homi算法

2.1.概率修剪策略

修剪策略大体上可分为2步：

• sampling： 计算概率数据 $P$，$P$ 由3元组 $(F,P_{stgy},P_{ratio})$ 构成。

  • $F$ 表示一个n维特征集合，每一维表示一个core branch condition，用来计算一个状态的特征向量。

  • $P_{stgy}$ 是n维向量 $\theta$ 的概率分布，$\theta$ 用于计算每个状态的分数。每次调用 $PRUNE(S,P,{\eta }_t)$ 都会根据 $P_{stgy}$ 重新sample出一个 $\theta$ 向量。

  • $P_{ratio}$ 是修剪比例 $r$ 的概率分布，$r$ 用于决定要修剪的状态数量。每次调用 $PRUNE(S,P,{\eta }_t)$ 都会根据 $P_{ratio}$ 重新sample出一个 $r$ 值。

• pruning：修剪函数如下面公式所示，说白了，就是选取bottom-k分数的状态修剪掉，k = |Sp * r|。

$$PRUNE(S,P,{\eta }_t)=\{\begin{array}{rcl}\underset{S_p\subseteq S\bigwedge |S_p|=S\ast r}{\mathrm{argmin}}\sum _{s\in S_p}score(s,\theta )& & if(F\ne \varnothing )\\ \varnothing & & otherwise\end{array}$$

上述过程针对每个状态：

• 首先将状态转换成1个特征向量，每个特征表示一个布尔谓词，用于检查状态 s 的路径条件 $\Phi$ 是否包含特定的分支条件 $\varphi$。形式化定义如下，即如果当前 s 的路径条件包括条件表达式 ${\varphi }_i$（${\varphi }_i$ 为 $F$ 中第i个core branch condition），那么特征向量第i维为1，否则为0。其完整特征向量 $feat(s)=<fea{t}_1(s),...,fea{t}_n(s)>$。

$$fea{t}_i(s)=\{\begin{array}{rcl}1& & if({\varphi }_{i}in\Phi )\\ 0& & otherwise\end{array}$$

• 之后通过概率分布 $P_{stgy}$ 可sample出 $\theta$，$score(s,\theta )=feat(s).\theta$。比如 $\theta =<0.4,-0.82,-0.3>,feat(s)=⟨1,0,0⟩$，那么 $score=0.4$。

• 然后从概率分布 $P_{ratio}$ sample出修剪状态的比例 $r$，修剪掉 bottom-|Sp * r| 的状态。

2.2.Homi

• Homi的关键点，算法2，是通过符号执行期间的online learning，不断更新特征和两个概率分布，$P_{stgy}$ 和 $P_{ratio}$。这一轮计算的概率数据 $P_{stgy}$ 和 $P_{ratio}$ 会在下一轮用来进行状态修剪。

• 在限定时间 $N$ 内，标准符号执行只运行一次 RUN 函数，而HOMI将 $N$ 分成多个时间片（不是平均分），每次运行 $N^{{}^{\prime }}$ 个时间单位。

• $\mu$ 是均匀分布。

在HOMI的运行过程中：

• $N^{{}^{\prime }},P_{stgy},P_{ratio}$ 均采用均匀分布随机初始化, $F$ 初始化为空集。因此第一轮 RUN，并不会进行状态修剪。

• $D$ 是由3元组 $<\Phi ,t,B>$ 构成的集合，第1个是路径条件，第2个是对应的测试用例，第3个是其覆盖的分支。

2.2.1.Collecting Promising Data

这一小节主要介绍算法2第10行 $GoodD\leftarrow Extract(D)$ 的过程。$GoodD$ 是 $D$ 的一个子集，意味着最有意义的测试用例构成的集合，它们满足以下条件：

• $GoodD$ 中所有用例的分支覆盖与 $D$ 中相同。

• $GoodD$ 最小化。

计算过程如下：

• $D^{\ast }=\underset{D^{{}^{\prime }}\subseteq D}{\mathrm{argmax}}\underset{(\_,\_,B)\in D^{{}^{\prime }}}{|\cup B|}$，找出所有能让分支覆盖率最大化的集合。

• $GoodD=\underset{D^{{}^{\prime }}\in D}{\mathrm{argmin}}|D^{{}^{\prime }}|$，选取最小的一个。

作者通过一个贪心算法实现上述过程。

2.2.2.Generating Features.

这部分对应算法2第11行 $NewF\leftarrow FGenerator(GoodD)$，也就是将 $GoodD$ 中的所有状态转换成对应特征向量。

作者首先定义一个core branch condition的概念，core branch condition $\varphi$ 可由下面语言推导出

$$L::=cond|cond\bigwedge cond|cond\bigvee cond$$

$$cond::=lv=n$$

$$lv::=\alpha |\alpha [i]$$

$l-value(lv)$ 表示一个符号值，或者符号数组的一个元素，$cond$ 为判定符号值是否等于一个常量的表达式。core branch condition可以为单个表达式或多个表达式构成的合取范式或者析取范式。

为了生成特征向量作者

• 首先从 $GoodD$ 中提取所有的路径条件组成集合 $PC$， P C = { Φ    ∣    ( Φ , _ , _ ) ∈ G o o d D } PC = \{\Phi \; | \; (\Phi, \_, \_) \in GoodD\} PC={Φ∣(Φ,_,_)∈GoodD}。

• 然后从 $PC$ 中提取所有的条件表达式组成集合 $NewF$， N e w F = { ϕ ∈ L    ∣    ϕ ∈ Φ , Φ ∈ P C } NewF = \{\phi \in L \; | \; \phi \in \Phi, \Phi \in PC\} NewF={ϕ∈L∣ϕ∈Φ,Φ∈PC}，$L$ 指前面能推导出core branch condition的语言。

假设有 P C = { { ( α = = 3 ) , ( α > 1 ) } , { ( α [ 2 ] , 3 ) , ( α [ 2 ] = = 8 ) } } PC = \{\{(\alpha == 3), (\alpha > 1)\}, \{(\alpha[2] , 3), (\alpha[2] == 8)\}\} PC={{(α==3),(α>1)},{(α[2],3),(α[2]==8)}}，那么提取的 $NewF=\{(\alpha ==3),(\alpha [2]==8)\}$。

其中示例集合 $NewF$ 中的两个特征是确定每个路径条件的模型的最小条件；例如，第一路径条件的模型 $\alpha ==3\bigwedge \alpha >1$ 可以简化成 $\alpha ==3$。简而言之，第11行生成的特征集 $NewF$ 代表了最小测试用例的关键证据，这些测试用例有助于最大化分支覆盖，直到当前状态。

可以看到，在循环的每一轮 $NewF$ 的维度都可能不一样，因此状态对应的特征向量在每一轮可能都维度不同。

2.2.3.Learning Distribution

在算法2第12行，$P_{stgy},P_{ratio},N^{{}^{\prime }}\leftarrow PGenerator(GoodD,NewF)$ 中 $PGenerator$ 会学习到向量 $\theta$ 和标量 $r$ 的概率分布 $P_{stgy},P_{ratio}$，输出的 $N^{{}^{\prime }}$ 会下个循环运行 RUN 的时间单位。

$P_{stgy}=<P_1,...,P_n>$，$P_i$ 为 $NewF$ 第i个特征对应的权重 ${\theta }^i$ 的概率。计算 $P_i$：

• 首先从 $GoodD$ 中选取所有的testcase组成 $GoodT$ 集合， G o o d T = { t    ∣    ( _ , t , _ ) ∈ G o o d D } GoodT = \{t \; | \;(\_,t,\_) \in GoodD\} GoodT={t∣(_,t,_)∈GoodD}。

• 其中算法会为每个testcase维护对应的四元组信息 $t=(F,\theta ,r,N^{{}^{\prime }})$。

  • $F$ 是testcase对应状态集合的特征向量集合，推测testcase遍历过的每个状态的特征向量都被提取了

  • $\theta$ 是对应权重向量

  • $r$ 是修剪比例

  • $N^{{}^{\prime }}$ 是时间分配

• 收集所有状态的特征向量集合 $GoodF=\underset{(F,\_,\_,\_)\in GoodT}{\cup }F$

• 接着，按如下方式计算 $P_i$，方便之后sample出 $\theta$:

  • $P_i=\{\begin{array}{rcl}N(\mu (W_i),\delta (W_i),-1,1)& & if({\varphi }_i^{new}\in GoodF)\\ u([-1,1])& & otherwise\end{array}$，${\varphi }_i^{new}$ 是 $NewF$ 中第i个条件，$N$表示截断正态分布，平均值 $\mu (W_i)$，标准差 $\delta (W_i)$，最大值1，最小值-1。$u$ 为均匀分布。

  • W i = { θ k    ∣    ( ϕ i n e w = ϕ k ) ⋀ ( { ϕ 1 , . . . , ϕ n } , θ , _ , _ ) ∈ G o o d T } W_i = \{\theta^k \; | \; (\phi_i^{new} = \phi_k) \bigwedge (\{\phi_1, ..., \phi_n\}, \theta, \_, \_) \in GoodT\} Wi​={θk∣(ϕinew​=ϕk​)⋀({ϕ1​,...,ϕn​},θ,_,_)∈GoodT}，这个公式有点难以理解，假设目前 $GoodT$ 中有3个testcase，目前 ${\varphi }_i^{new}$ 在这3个testcase中分别为路径条件上第1，2，3个core branch condition，在生成testcase时，这3个示例可能对应3个不同的向量 $\theta$（因为每次状态修剪都会重新sample一个 $\theta$），记为 ${\theta }_1,{\theta }_2,{\theta }_3$。那么此时 W i = { θ 1 1 , θ 2 2 , θ 3 3 } W_i = \{\theta^1_1, \theta^2_2, \theta^3_3\} Wi​={θ11​,θ22​,θ33​}（${\theta }_j^i$ 表示向量 ${\theta }_j$ 第i维度的值）。

  • $u(W)=\sum _{w\in W}\frac{w}{|W|}$, $\delta (W)=\sqrt{\frac{\sum _{w\in W}(w-u(W){)}^2}{|W|}}$

• 按上述步骤，可以求出 $P_{stgy}$ 中每一项的概率分布，然后求 $P_{ratio}$ 的分布:
  $P_{ratio}(X=r^{{}^{\prime }})=\frac{|\{(\_,\_,r,\_)\in GoodT|r^{{}^{\prime }}=r\}|}{|GoodT|}$，这个概率分布会之后用来sample出 $r$

• 再用同样的方式计算概率分布 $P_{time}$，方便之后sample出 $N^{{}^{\prime }}$

2.2.4.Sampling Values

这一步是基于 $P_{stgy}$ 和 $P_{ratio}$ sample出 $\theta$ 和 $r$。生成 $\theta$ 的方法采用下面3个方法之一：

• Exploitation，从 $P_{stgy}$ 中先sample出exploit向量: $Sampl{e}_{exploit}(P_1\times ...\times P_n)=<{\theta }^1,...,{\theta }^n>$

• Reverse Exploitation, 逆向sample出向量 ${\theta }_r$

  • U = { r 1 , r 2 , . . . , r 100    ∣    r i ∼ u ( − 1 , 1 ) } U = \{r_1, r_2, ..., r_{100} \; | \; r_i \sim u(-1, 1)\} U={r1​,r2​,...,r100​∣ri​∼u(−1,1)}，用均匀分布sample出100维向量 $U$。

  • $Sampl{e}_{reverse}(P_1\times ...\times P_n,U)=<{\theta }_r^1,...,{\theta }_r^n>$，${\theta }_r^i=\underset{u\in U}{\mathrm{argmax}}(u-{\theta }^i)$

• Exploration: 采用均匀分布采样的方法 $u([-1,1{]}^n)$ sample出 $\theta$

最后从概率分布 $P_{ratio}$ 和 $P_{time}$ 中sample出 $r$ 和下次运行 RUN 的时间 $N^{{}^{\prime }}$（$N^{{}^{\prime }}$ 的值每次从 200, 400, 600, 800 中随机选择一个）。

2.2.5.总结

可以看出，HOMI的运行流程就是循环下面过程：

• 基于上一轮（第1轮不进行状态修剪）计算的概率数据 $(F,P_{stgy},P_{ratio})$ 运行 RUN 的时候进行状态修剪。

  • $P_{stgy}$ 用来sample出n维向量（n是 $F$ 中core branch condition数量）$\theta$。

  • $P_{ratio}$ 用来sample出修剪比例 $r$。

  • $F$ 用来给每一个状态 $s$ 计算特征向量 $feat(s)$, $feat(s).\theta$ 即 $s$ 的分数，选取分数最低的 $k$ 个状态修剪掉。($k=|S|.r$)

• 运行完毕后会产生testcase集合 $T^{{}^{\prime }}$，从 $T^{{}^{\prime }}$ 选出满足最小并且能达到和 $T^{{}^{\prime }}$ 同样分支覆盖率的子集合 $Good{T}^{{}^{\prime }}$。

• 从 $Good{T}^{{}^{\prime }}$ 中提取core branch condition集合 $F^{{}^{\prime }}$。

• 基于 $F^{{}^{\prime }},Good{T}^{{}^{\prime }}$ 计算新的概率分布 $P_{stgy}^{{}^{\prime }},P_{ratio}^{{}^{\prime }}$。

• $(F^{{}^{\prime }},P_{stgy}^{{}^{\prime }},P_{ratio}^{{}^{\prime }})$ 会在下一轮用来进行状态修剪。

总的来说，作者的目标是找出一组能不断提高测试用例分支覆盖率的参数。

3.实验

探究的问题包括：

• 有效性：HOMI对提升分支覆盖率的效果如何？有多少bug只被HOMI发现了？

• 状态数量：与普通符号执行工具相比，HOMI在运行时维护多少状态？

• 与朴素方法的对比：与随机状态修剪相比，HOMI表现如何？

3.1.实验设置

使用了9个GNU开源程序，一些统计信息如下表所示：

程序名	总行数	分支数
gawk-3.1.4	60904	11934
grep-2.6	56931	7021
combine-0.4.0	35756	2359
grep-2.6	56931	7021
ginstall (8.31)	22290	3652
ptx (8.31)	22148	5262
vdir (8.31)	19378	3830
pr (8.31)	12156	1991
dd (8.31)	10531	1547

选用的baseline包括：

• 标准符号执行（不带状态修剪策略），分别采用9种不同的状态搜索策略：

  • CPICount (CallPath Instruction Count, nurs:cpicnt)

  • CovNew (nurs:covnew)

  • MinDistance (Minimal Distance to Uncovered, nurs: md2u)

  • InstrCount (Instruction Count, nurs:icnt)

  • QueryCost (nurs:qc)

  • RandomPath (random-path)

  • Depth (nurs:depth)

  • RandomState (random-state)

  • RoundRobin (klee默认)

其它设定包括（针对每个程序的运行）

• 运行参数：--sym-args 0 1 10 --sym-args 0 2 2 --sym-files 1 8 --sym-stdin 8 --sym-stdout

• 内存限制：2GB

• 时间限制：5小时

3.2.有效性

下图反映了HOMI+covnew与标准符号执行+5个策略的对比结果

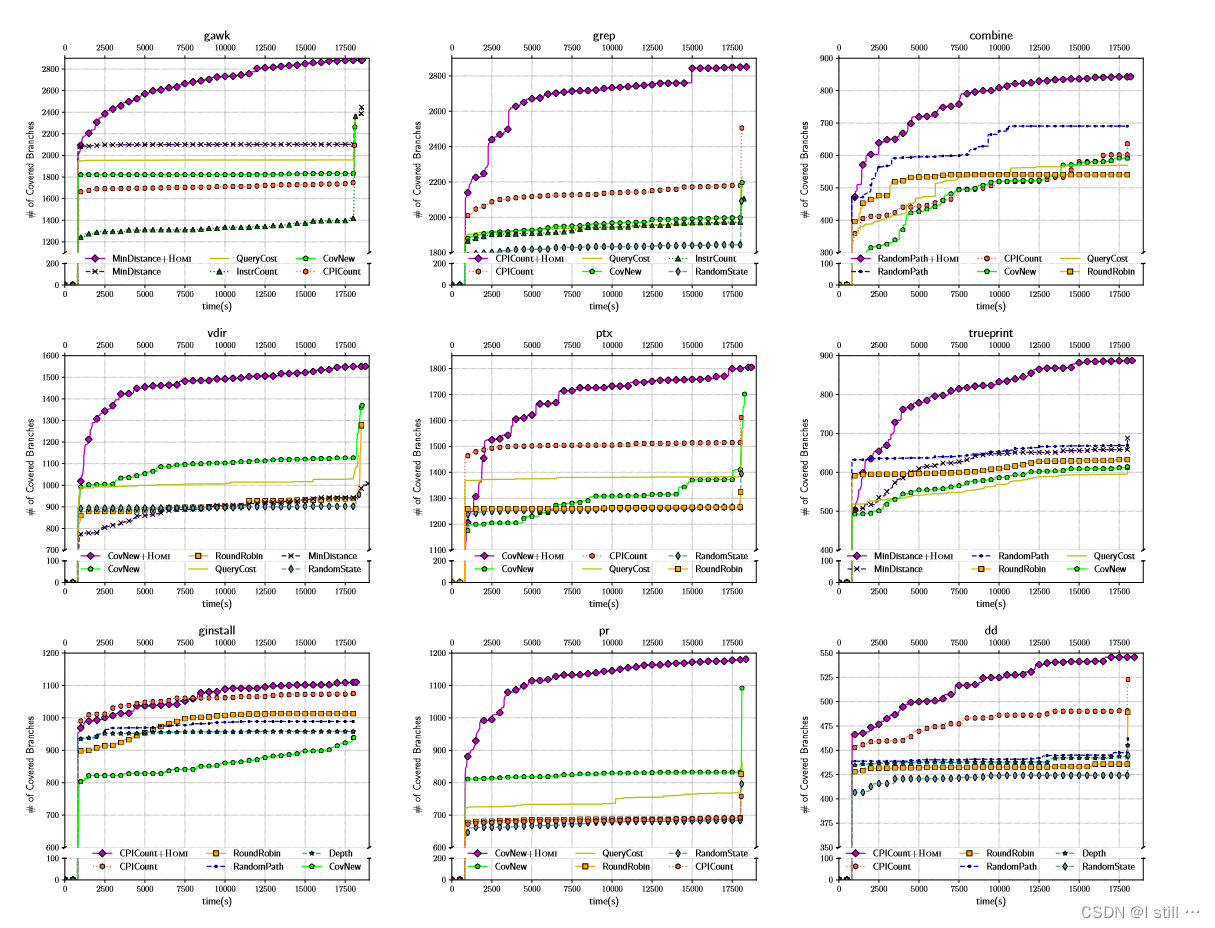
下表展示了仅由HOMI结合表现最佳的搜索策略（BestH）以及标准符号执行结合排名前5的搜索策略（xthH）覆盖到的分支的数量。

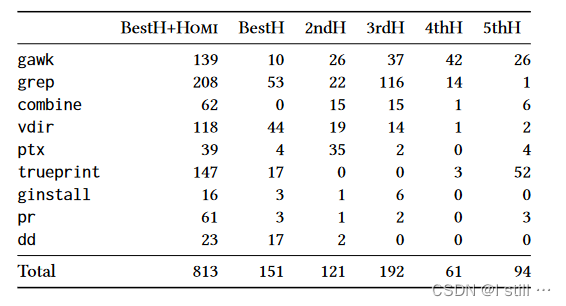
下表展示了表现最好的2种搜索策略结合与不结合HOMI的bug查找能力的对比

3.3.候选状态数量

下表展示了不同策略每一时刻状态列表的长度，紫线为MinDistance+HOMI，其它为标准符号执行结合不同搜索策略。

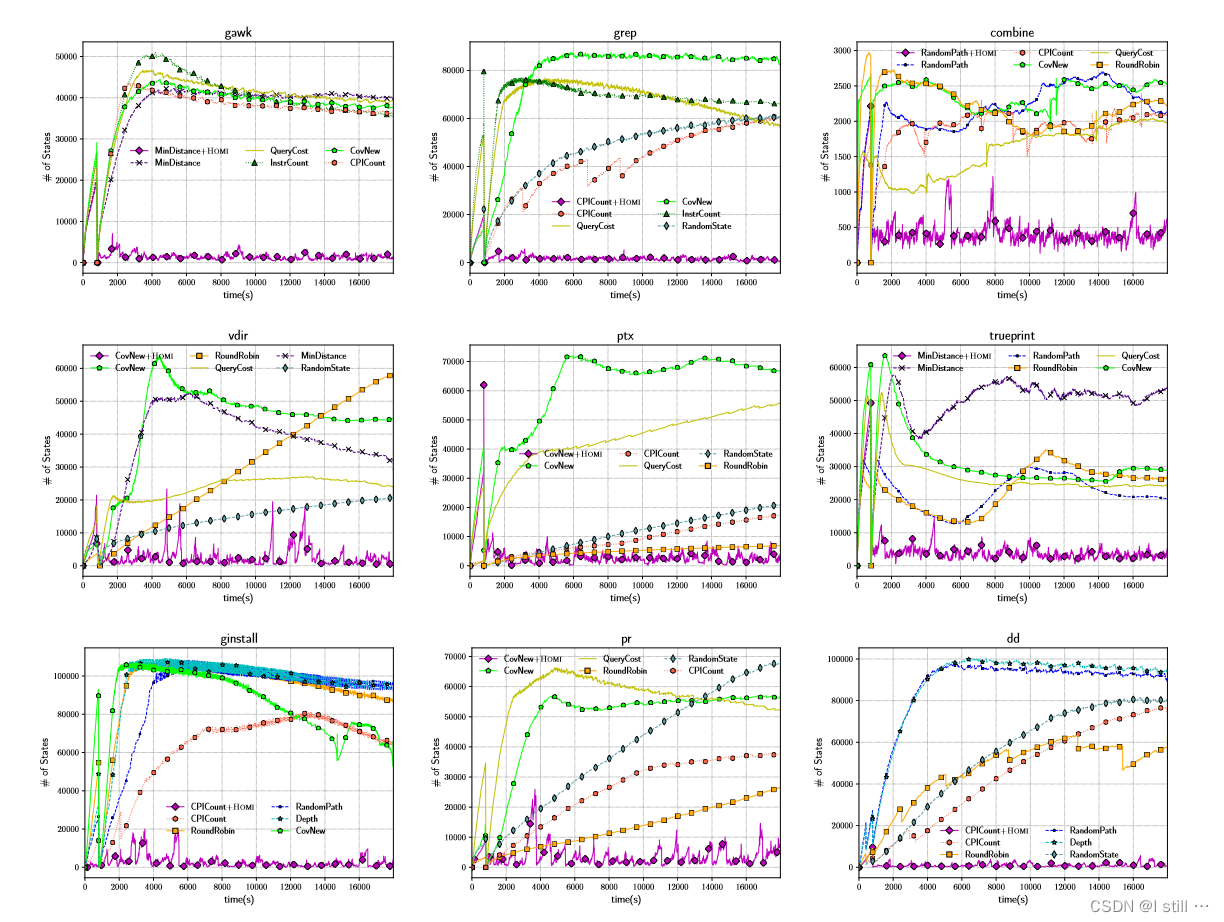
3.4.与朴素方法的对比

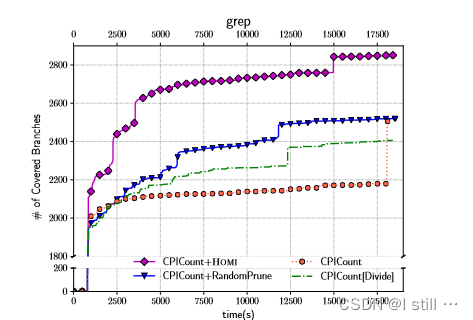
下表反映了HOMI+CPICNT与Random+CPICNT（随机状态修剪），CPICNT，CPICNT（divide）的对比

4.代码实操

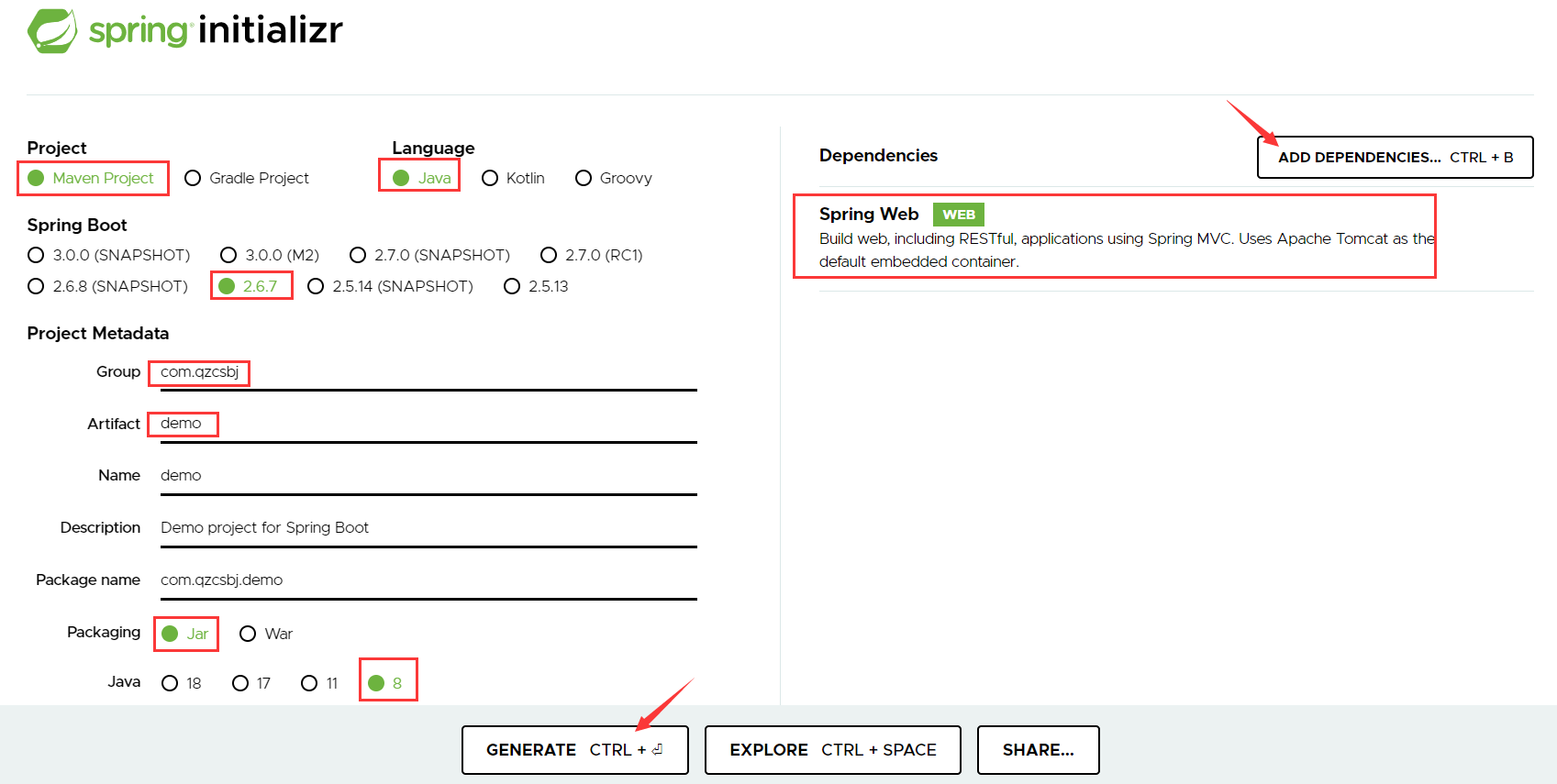
Homi的github地址，作者提供了一个20G的vdi虚拟硬盘，用virtualbox打开，可以省去配环境的麻烦，并且里面klee和benchmark已经编译好了。作者的环境为：

• klee-2.0

• LLVM 6.0.0

整个Homi的文件夹组织为：

• script: python脚本都存放在这个目录下

• klee: 作者修改后的klee项目目录

• experiments: 存放实验中间文件和各种输出文件的目录

• benchmarks: 存放各种数据集

代码实操主要以 trueprint 这个程序为示例介绍，作者给出运行的命令如下：

• cd ~/Homi/script

• python3 Homi.py pgm_config/1trueprint.json 3600 homi nurs:md2u 1

  • pgm_config/1trueprint.json 包含各种文件路径，内容如下（当前路径为 ~/Homi/script）：

  {
  "pgm_name": "trueprint", # 程序名
  "pgm_dir": "../benchmarks/trueprint-5.4/obj-llvm/", # llvm编译路径
  "exec_dir": "/src", # 可执行文件的子路径
  "gcov_path": "../benchmarks/trueprint-5.4/1obj-gcov/src/", # gcov存放路径
  "gcov_file": "../*/*.gcov", # gcov文件路径模式
  "gcda_file": "../*/*.gcda" # gcda文件路径模式
  } 
  

  • 3600 为符号执行该程序的时间限制，单位秒。

  • homi 表示运行homi，与之对应的参数是 klee，表示运行普通符号执行。

  • nurs:md2u 表示选择的搜索策略。

  • 1 表示实验次数，主要是用来构建中间文件名称用，其它并没有什么实际作用。

Homi.py 的 main 函数核心部分如下：

if tool=="homi":         
    # Homi performs the general symbolic execution without state-pruning on the first iteration.
    Run_KLEE(pgm_config, pgm, stgy, total_time, small_time, ith_trial, iters, tool, d_name, Space_time)  
        
    while iters<100:
        dir_name, Data = Run_gcov(load_config, pgm, stgy, iters, tool, ith_trial, Data, d_name)
        topk_testcases = SetCoverProblem(Data, iters)
        features = Feature_Extractor(pgm, stgy, dir_name, topk_testcases, ith_trial, iters)
        small_time= PruningStgy_Generator(load_config, pgm, stgy, ith_trial, features, dir_name, topk_testcases, iters, Space_time)
            
        iters=iters+1
        Run_KLEE(pgm_config, pgm, stgy, total_time, small_time, ith_trial, iters, tool, d_name, Space_time)
else:
    for num in range(1,100):
        Run_KLEE(pgm_config, pgm, stgy, total_time, small_time, ith_trial, iters, tool, d_name, Space_time) 
        iters=iters+1

• Run_KLEE 对应paper算法2中第7行的 RUN 函数，不过代码里作者换了1种写法，在 while 循环外先 RUN 一次，然后循环体内第1句到倒数第2句都是收集 $(F^{{}^{\prime }},P_{stgy}^{{}^{\prime }},P_{ratio}^{{}^{\prime }})$ 为下一次状态修剪做准备。

• Run_gcov 对应算法2 8-9行 $D$ 的收集过程。

• SetCoverProblem 对应算法2 第10行 $GoodD\leftarrow Extract(D)$。算法输出的是一个 list，每个元素是一个testcase名称，str 类型，诸如 x_tc_dir/test000001.ktest 形式。

• Feature_Extractor 对应算法2 第11行 $NewF\leftarrow FGenerator(GoodD)$。

• PruningStgy_Generator 对应算法2 第12行 $P_{stgy},P_{ratio},N^{{}^{\prime }}\leftarrow PGenerator(GoodD,NewF)$。

在参数和返回值方面：

• dir_name 为中间文件夹路径，在该示例中为 result_All/{x}homi_trueprint_nurs:md2u_tc_dir，{x} 表示实验轮次。dir_name 为 ~/Homi/experiments 下的相对路径，用来存放各种输出文件。

• Space_time 为硬编码的参数，为 [200, 400, 600, 800]

• small_time 对应paper中的 $N^{{}^{\prime }}$，初始为 800。

• Data 为 Dict[str, Set[int]] 类型，对应paper中的 $D$。

  • key为testcase的相对路径，比如 test000001.ktest 对应的key为 x_tc_dir/test000001.ktest，x 为循环次数，如果这次是第1次运行 Run_gcov 那就是 1_tc_dir/test000001.ktest，value为该testcase覆盖的branch行数。

  • 在paper中，$D$ 为一个 set，元素为 $(\varphi ,t,B)$（路径条件，测试用例，覆盖的branch）

• topk_testcases 为 List[str]，对应 $GoodD$，不过只保存了名字。

• features 对应 $F^{{}^{\prime }}$。

4.1.代码运行

命令行运行 python3 Homi.py pgm_config/1trueprint.json 3600 homi nurs:md2u 1，运行结束后 experiments 下的目录结构如下：

../experiments
├── homi__nurs:md2u0
│   └── trueprint
├── homi__nurs:md2u1
│   └── trueprint
├── homi__nurs:md2u2
│   └── trueprint
├── homi__nurs:md2u3
│   └── trueprint
├── homi__nurs:md2u4
│   └── trueprint
├── homi__nurs:md2u5
│   └── trueprint
├── homi__nurs:md2u6
│   └── trueprint
└── result_All
    └── 1homi_trueprint_nurs:md2u_tc_dir
        ├── 0__tc_dirs
        ├── 1__tc_dirs
        ├── 2__tc_dirs
        ├── 3__tc_dirs
        ├── 4__tc_dirs
        ├── 5__tc_dirs  
        ├── 6__tc_dirs      

其中

• 从文件夹数量来看，循环进行了7次（Feature_Generator）运行了7次。

• homi__nurs:md2u{i}/trueprint 为空目录，这个目录主要是创建来把benchmark编译后的文件复制进来，每次运行 Run_KLEE 的时候都会生成一个 homi__nurs:md2u{i}/trueprint 目录并把benchmark复制进来，符号执行便在 homi__nurs:md2u{i}/trueprint 目录下进行，{i} 指第i次循环，执行完后会执行 cp -r klee-out-0 Homi/experiments/result_All/1homi_trueprint_nurs:md2u_tc_dir/{i}__tc_dirs 将生成的testcase等文件复制到 result_All 文件夹下并清空 homi__nurs:md2u{i}/trueprint 目录。

• result_All/1homi_trueprint_nurs:md2u_tc_dir 下有1个 1homi_trueprint_nurs:md2u_pruning_ratio 文件，表示最新一轮 PruningStgy_Generator 后sample出的 $r$ 值，但是里面保存了50个值，在运行1次 $RUN$ 时会进行多次状态修剪，每次修剪都会用到不同的 $r$ 值。在原paper算法1中，$r$ 理论上每次执行 $Prune$ 的时候sample出1个。

• result_All/1homi_trueprint_nurs:md2u_tc_dir/weights/{i}trial 下保存了 50 个w文件，每一个对应1个 $\theta$ 向量，每次进行状态修剪会用到不同的 $\theta$ 向量。在原paper算法1中，$\theta$ 理论上每次执行 $Prune$ 的时候sample出1个。

• result_All/1homi_trueprint_nurs:md2u_tc_dir 下有1个 1homi_trueprint_nurs:md2u_feature_data 文件，保存的应该是最新一轮 Feature_Extractor 之后生成的特征集合 $F^{{}^{\prime }}$，内容放在最下面了，每一行对应一个core branch condition，str 类型。

• result_All/1homi_trueprint_nurs:md2u_tc_dir/weights 下有7个 feature_data 文件，对应每一轮 Feature_Extractor 生成的特征集合。

4.2.Run_KLEE

python脚本部分参考 Homi.py – Run_KLEE ，Run_KLEE.py，其中 gen_run_cmd 函数拼凑出运行klee的命令，在示例中为: Homi/klee/build/bin/klee -trial=0 --max-memory=2000 --watchdog -max-time=800 -dirname=~/Homi/experiments/result_All -write-kqueries -only-output-states-covering-new --simplify-sym-indices --output-module=false --output-source=false --output-stats=false --disable-inlining --use-forked-solver --use-cex-cache --libc=uclibc --posix-runtime -env-file=~/Homi/klee/build/../test.env --max-sym-array-size=4096 --max-instruction-time=30 --switch-type=internal --use-batching-search --batch-instructions=10000 -ignore-solver-failures --search=nurs:md2u trueprint.bc --sym-args 0 1 10 --sym-args 0 2 2 --sym-files 1 8 --sym-stdin 8 --sym-stdout

接下来看 Executor.cpp run函数，首先读取上一轮计算好的 $F^{{}^{\prime }}$ 和 $P_{ratio}$。

if(Homi){ 
     Generate a set of features. 
    feat_id_map_=read_feature(dirname, naming);
    pratio_vec_=read_pruningratio(dirname, naming);
}

• feat_id_map_ 对应 $F^{{}^{\prime }}$，是一个 map<string, unsigned int>，key为core branch condition对应的字符串，value为该condition在特征集合中的索引好，最下面的 feature_data 文件对应的 feat_id_map_ 为 {"(Eq 46 (Read w8 1 arg02))": 0, "(Eq 49 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))": 1, ...}

• pratio_vec_ 是一个 vector<unsigned>， 长度为50。前面说过，代码中为了方便不是严格意义上在 $RUN$ 中用 $P_{ratio}$ 采样，而是先采样50个 $r$ 值，然后修剪状态时轮着用，因此 pratio_vec_ 对应50个不同的 $r$ 值。

同时在代码中

• 每秒（prev_time 变量就是为了这个）都会采样当前状态列表长度，打印到 state_data 文件中，并且运行的时候每30秒并且状态列表长度大于500时才进行修剪，而不是像paper 算法1中每次选择状态之前都修剪。

• 修剪状态时，先从 weights/{i}trials 文件夹下读取 w 文件中的 $\theta$ 向量（对应变量 wvector_，vector<double> 类型），而不是读取 $P_{stgy}$ 再采样，同样的，执行klee时已经从 $P_{stgy}$ 时采样了50个 $\theta$ 向量轮着用。

• fv_vecs = extract_feature(states, feat_id_map_); 根据 $\theta$ 和计算每个状态的特征向量，fv_vecs 为 vector<vector<int>> 类型，一般第1维是状态数量，第2维是特征长度。

  • extract_feature 对应paper中计算 $feat(s)$ 的部分，如果 feat_id_map_ 第i个condition出现在状态 s 的路径约束中，那么 $fea{t}_i(s)=1$，反之为 $0$。

  • extract_feature 最后一行会记录一个冗余特征索引，如果1个特征对所有得状态都是0或1，那这个特征是冗余特征。因此 fv_vecs 的最后1个向量记录的是冗余特征索引。

• prune_states(wv_name, fv_vecs, wvector_, pruning_ratio); 进行状态修剪。

  • prune_states 返回值是被修剪得状态数量，如果有效特征维度（core branch condition）数量太小（特征数-冗余特征数 <= 5）那就不进行状态修剪。

  • 修剪状态的方式就是调用 terminateStateEarly，对于 terminateStateEarly 生成的testcase，klee会输出一个 .early 文件，里面记录 message，被修剪状态的 message 是learning_data字符串，里面记录了冗余特征索引、修剪比率 $r$、采用的向量 $\theta$。

剩下就是正常进行符号执行。

4.3.Run_Gcov

这一部分对应算法2 8-9行 $D$ 的收集过程，返回值 Data 为 Dict[str, Set[int]] 型，key为testcase文件名，value为该testcase独自覆盖到的分支（分支用gcov文件行号标识，最下面有gcov文件示例）。

• 首先，Run_Gcov 会计算一个 d_tc_data 变量，该变量为 dict，将每个testcase文件路径映射为一个四元组 [budget, pratio, l_rfeats, wvector]，即该testcase生成时klee运行时间限制($N^{{}^{\prime }}$)、修剪比率 $r$，冗余特征索引、向量 $\theta$ 存储的文件路径。

• 然后，Run_Gcov对每个testcase：

  • 运行klee-replay。生成gcda文件。

  • 运行gcov -b xxx.gcda，生成对应gcov文件。

  • 解析gcov文件，找出该testcase覆盖到的分支，具体过程可参考CalCoverage。6.3部分给出了一个gcov示例，在gcov文件中，branch 开头的行代表一条分支，never 表示对应条件判断语句没被执行过，taken 0% 表示条件语句执行过但是没覆盖过该分支。在计算分支覆盖率时用gcov文件行号来标识一个分支。

  • 将该testcase覆盖情况写入变量 Data。

运行完 Run_Gcov 后接下来会通过 SetCoverProblem 生成 $GoodD$，返回值 topk_testcases 为 List[str] 型，记录 $GoodD$ 每一个testcase对应的文件路径。

4.4.Feature_Extractor

在运行klee时，作者添加了 -write-kqueries 参数，因此每个testcase都会生成一个对应的 kquery 文件，保存对应的路径约束。这篇blog最底部有个 kquery 文件示例。

Feature_Extractor 则是通过遍历一个testcase的 kquery 文件生成 $F^{{}^{\prime }}$（$F^{{}^{\prime }}$ 对应代码中的 feat_set，为 Set[str] 类型），每一个core branch condition应该为 Eq ... arg ... 这样的 str。一次最多提取200个core branch condition。

最后，将 feat_set dump到一个 {i}homi_trueprint_nurs:md2u_feature_data 文件中（i 为实验轮次），这个文件每轮循环都会被覆盖。

4.5.PruningStgy_Generator

相当于 $PGenerator(GoodD,NewF)$。这部分用到了一个全局变量 tried_wv，该变量将.w文件路径映射为该文件中的向量 $\theta$。

在paper中，作者提到了3种 $(P_{stgy},P_{ratio})$ 生成方案：exploit, reverse_exploit, explore。其中explore几乎等同于随机概率选择，并没有用到之前计算的特征值。对于生成方案的选择，作者选用以下策略：

• 如果循环次数在10次以内，那么选择explore方案。

• 其它情况从3种方案种随机选择一种方案。

对于explore方案，其 $\theta$ 生成代码对应333行 weights = [str(random.uniform(lower, upper)) for _ in range(len(features))] ，即 $\theta$ 每一维度都是在 -1, 1之间均匀随机选择。

对于剩下2种方案，首先根据 Run_Gcov 生成的 d_tc_data 计算变量 d_feat_wvs，该变量对应paper中3.2.3的 $W$，将没有成为冗余特征的core branch condition（str 类型，比如 (Eq 46 (Read w8 1 arg02))）映射为在 $GoodD$ 中出现过的所有权重。对于core branch condition $i$（即特征集合第 $i$ 个特征），d_feat_wvs[i] 对应 $W_i$。剩下的代码则是按照论文所说的方法直接sample出50个 $\theta$ 向量。

5.参考文献

Cha S , Oh H . Making symbolic execution promising by learning aggressive state-pruning strategy[C]// ESEC/FSE '20: 28th ACM Joint European Software Engineering Conference and Symposium on the Foundations of Software Engineering. ACM, 2020.

6.其它示例

6.1.kquery

代码

#include <klee/klee.h>

int main() {
  int a, b, c, res;
  klee_make_symbolic(&a, sizeof(a), "a");
  klee_make_symbolic(&b, sizeof(b), "b");
  klee_make_symbolic(&c, sizeof(c), "c");
  if (a <= 0)
      a = a + 10;
  else
      a = a - 10;
  
  if (a <= b)
      res = a - b;
  else
      res = a + b;
  
  if (res > c)
      res = 1;
  else
      res = 0;
  return 0;
}

kquery:

对应 false --> false --> true 分支的kquery文件内容如下，前3行为输入变量，下面则是kquery语句（）

array a[4] : w32 -> w8 = symbolic
array b[4] : w32 -> w8 = symbolic
array c[4] : w32 -> w8 = symbolic
(query [
(Eq false (Sle N0:(ReadLSB w32 0 a) 0))
(Eq false (Sle (Add w32 4294967286 N0) N1:(ReadLSB w32 0 b))) 
(Slt (ReadLSB w32 0 c) (Add w32 4294967286 (Add w32 N0 N1)))
] false)

6.2.feature_data内容

(Eq 46 (Read w8 1 arg02))
(Eq 49 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 43 (Read w8 8 arg00))
(Eq 43 (Read w8 7 arg00))
(Eq 52 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 90 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 67 (Extract w8 0 (SExt w32 (Read w8 2 arg00))))
(Eq 46 (Read w8 2 arg00))
(Eq 1 (Read w8 4 arg00))
(Eq 116 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 0 (Read w8 2 arg00))
(Eq 0 (Read w8 7 arg00))
(Eq 101 (Read w8 3 arg00))
(Eq 118 (Read w8 9 arg00))
(Eq 64 (Read w8 6 arg00))
(Eq 97 (Read w8 8 arg00))
(Eq 64 (Read w8 7 arg00))
(Eq 111 (Read w8 7 arg00))
(Eq 103 (Read w8 6 arg00))
(Eq 61 (Read w8 9 arg00))
(Eq 114 (Extract w8 0 (SExt w32 (Read w8 1 arg02))))
(Eq 120 (Read w8 8 arg00))
(Eq 46 (Read w8 3 arg00))
(Eq 1 (Read w8 0 arg02))
(Eq 112 (Read w8 8 arg00))
(Eq 0 (Read w8 1 arg01))
(Eq 105 (Read w8 7 arg00))
(Eq 100 (Read w8 5 arg00))
(Eq 72 (Read w8 9 arg00))
(Eq 45 (Read w8 0 arg00))
(Eq 100 (Read w8 9 arg00))
(Eq 72 (Read w8 7 arg00))
(Eq 108 (Read w8 2 arg00))
(Eq 107 (Read w8 8 arg00))
(Eq 45 (Read w8 0 arg01))
(Eq 115 (Read w8 9 arg00))
(Eq 0 (Read w8 1 arg02))
(Eq 32 (Read w8 2 arg00))
(Eq 52 (Extract w8 0 (SExt w32 (Read w8 1 arg02))))
(Eq 74 (Extract w8 0 (SExt w32 (Read w8 3 arg00))))
(Eq 111 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 109 (Read w8 7 arg00))
(Eq 76 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 117 (Read w8 5 arg00))
(Eq 46 (Read w8 8 arg00))
(Eq 104 (Read w8 8 arg00))
(Eq 115 (Read w8 6 arg00))
(Eq 111 (Read w8 3 arg00))
(Eq 76 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 104 (Read w8 1 arg02))
(Eq 117 (Read w8 4 arg00))
(Eq 115 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 119 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 120 (Read w8 9 arg00))
(Eq 0 (Read w8 5 arg00))
(Eq 99 (Read w8 9 arg00))
(Eq 114 (Read w8 7 arg00))
(Eq 51 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 1 (Read w8 2 arg00))
(Eq 109 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 100 (Read w8 2 arg00))
(Eq 117 (Read w8 6 arg00))
(Eq 108 (Read w8 4 arg00))
(Eq 104 (Read w8 7 arg00))
(Eq 64 (Read w8 9 arg00))
(Eq 45 (Read w8 9 arg00))
(Eq 0 (Read w8 4 arg00))
(Eq 66 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 0 (Read w8 9 arg00))
(Eq 84 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 116 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 0 (Read w8 3 arg00))
(Eq 89 (Extract w8 0 (SExt w32 (Read w8 4 arg00))))
(Eq 103 (Read w8 8 arg00))
(Eq 61 (Read w8 8 arg00))
(Eq 45 (Read w8 1 arg00))
(Eq 87 (Extract w8 0 (SExt w32 (Read w8 2 arg00))))
(Eq 99 (Read w8 2 arg00))
(Eq 100 (Read w8 7 arg00))
(Eq 111 (Read w8 8 arg00))
(Eq 117 (Extract w8 0 (SExt w32 (Read w8 2 arg00))))
(Eq 46 (Read w8 0 arg00))
(Eq 32 (Read w8 5 arg00))
(Eq 43 (Read w8 3 arg00))
(Eq 118 (Read w8 0 arg02))
(Eq 61 (Read w8 4 arg00))
(Eq 98 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 102 (Read w8 7 arg00))
(Eq 103 (Read w8 5 arg00))
(Eq 108 (Read w8 7 arg00))
(Eq 110 (Extract w8 0 (SExt w32 (Read w8 4 arg00))))
(Eq 106 (Read w8 7 arg00))
(Eq 1 (Read w8 0 arg00))
(Eq 45 (Read w8 0 arg02))
(Eq 46 (Read w8 4 arg00))
(Eq 97 (Read w8 7 arg00))
(Eq 51 (Extract w8 0 (SExt w32 (Read w8 1 arg02))))
(Eq 99 (Read w8 8 arg00))
(Eq 114 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 98 (Read w8 5 arg00))
(Eq 101 (Read w8 8 arg00))
(Eq 116 (Read w8 6 arg00))
(Eq 88 (Extract w8 0 (SExt w32 (Read w8 3 arg00))))
(Eq 103 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 119 (Read w8 7 arg00))
(Eq 108 (Read w8 6 arg00))
(Eq 37 (Read w8 6 arg00))
(Eq 46 (Read w8 7 arg00))
(Eq 120 (Read w8 4 arg00))
(Eq 101 (Read w8 9 arg00))
(Eq 101 (Read w8 7 arg00))
(Eq 68 (Read w8 7 arg00))
(Eq 45 (Read w8 8 arg00))
(Eq 109 (Read w8 9 arg00))
(Eq 50 (Extract w8 0 (SExt w32 (Read w8 1 arg02))))
(Eq 112 (Read w8 9 arg00))
(Eq 87 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 112 (Read w8 6 arg00))
(Eq 99 (Read w8 7 arg00))
(Eq 106 (Read w8 6 arg00))
(Eq 72 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 68 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 104 (Read w8 9 arg00))
(Eq 97 (Read w8 9 arg00))
(Eq 46 (Read w8 5 arg00))
(Eq 45 (Read w8 7 arg00))
(Eq 67 (Read w8 7 arg00))
(Eq 61 (Read w8 5 arg00))
(Eq 84 (Read w8 7 arg00))
(Eq 115 (Read w8 8 arg00))
(Eq 115 (Read w8 0 arg02))
(Eq 71 (Extract w8 0 (SExt w32 (Read w8 1 arg00))))
(Eq 37 (Read w8 7 arg00))
(Eq 120 (Read w8 3 arg00))
(Eq 111 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 46 (Read w8 6 arg00))
(Eq 97 (Read w8 3 arg00))
(Eq 118 (Read w8 8 arg00))
(Eq 108 (Read w8 9 arg00))
(Eq 98 (Extract w8 0 (SExt w32 (Read w8 3 arg00))))
(Eq 37 (Read w8 9 arg00))
(Eq 47 (Read w8 4 arg00))
(Eq 46 (Read w8 1 arg00))
(Eq 46 (Read w8 1 arg01))
(Eq 115 (Read w8 5 arg00))
(Eq 112 (Read w8 7 arg00))
(Eq 46 (Read w8 0 arg01))
(Eq 110 (Read w8 4 arg00))
(Eq 97 (Read w8 4 arg00))
(Eq 98 (Read w8 4 arg00))
(Eq 120 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 50 (Extract w8 0 (SExt w32 (Read w8 1 arg01))))
(Eq 49 (Extract w8 0 (SExt w32 (Read w8 1 arg02))))
(Eq 67 (Read w8 9 arg00))

gcov示例

用 gcov -b 生成对应的gcov文件。

       80:  315:	      if (n == (size_t) -2)
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
        -:  316:		{
        -:  317:# if SUPPORT_OLD_MBRTOWC
    #####:  318:		  state = backup_state;
        -:  319:# endif
    #####:  320:		  break;
        -:  321:		}
       80:  322:	      if (n == (size_t) -1)
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
        -:  323:		{
        -:  324:		  /* Remember that we read a byte, but don't complain
        -:  325:		     about the error.  Because of the decoding error,
        -:  326:		     this is a considered to be byte but not a
        -:  327:		     character (that is, chars is not incremented).  */
    #####:  328:		  p++;
    #####:  329:		  bytes_read--;
        -:  330:		}
        -:  331:	      else
        -:  332:		{
       80:  333:		  if (n == 0)
branch  0 taken 1% (fallthrough)
branch  1 taken 99%
        -:  334:		    {
        1:  335:		      wide_char = 0;
        1:  336:		      n = 1;
        -:  337:		    }
       80:  338:		  p += n;
       80:  339:		  bytes_read -= n;
       80:  340:		  chars++;
       80:  341:		  switch (wide_char)
branch  0 taken 1%
branch  1 taken 0%
branch  2 taken 1%
branch  3 taken 95%
branch  4 taken 0%
branch  5 taken 3%
        -:  342:		    {
        1:  343:		    case '\n':
        1:  344:		      lines++;
        -:  345:		      /* Fall through. */
        1:  346:		    case '\r':
        -:  347:		    case '\f':
        1:  348:		      if (linepos > linelength)
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
    #####:  349:			linelength = linepos;
        1:  350:		      linepos = 0;
        1:  351:		      goto mb_word_separator;
        1:  352:		    case '\t':
        1:  353:		      linepos += 8 - (linepos % 8);
        1:  354:		      goto mb_word_separator;
       76:  355:		    case ' ':
       76:  356:		      linepos++;
        -:  357:		      /* Fall through. */
        -:  358:		    case '\v':
       78:  359:		    mb_word_separator:
       78:  360:		      words += in_word;
       78:  361:		      in_word = false;
       78:  362:		      break;
        2:  363:		    default:
        2:  364:		      if (iswprint (wide_char))
branch  0 taken 50% (fallthrough)
branch  1 taken 50%
        -:  365:			{
        1:  366:			  int width = wcwidth (wide_char);
call    0 returned 100%
        1:  367:			  if (width > 0)
branch  0 taken 100% (fallthrough)
branch  1 taken 0%
        1:  368:			    linepos += width;
        1:  369:			  if (iswspace (wide_char))
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
    #####:  370:			    goto mb_word_separator;
        1:  371:			  in_word = true;
        -:  372:			}
        2:  373:		      break;
        -:  374:		    }
        -:  375:		}
        -:  376:	    }
       80:  377:	  while (bytes_read > 0);
branch  0 taken 88%
branch  1 taken 13% (fallthrough)
        -:  378:
        -:  379:# if SUPPORT_OLD_MBRTOWC
       10:  380:	  if (bytes_read > 0)
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
        -:  381:	    {
    #####:  382:	      if (bytes_read == BUFFER_SIZE)
branch  0 never executed
branch  1 never executed
        -:  383:		{
        -:  384:		  /* Encountered a very long redundant shift sequence.  */
    #####:  385:		  p++;
    #####:  386:		  bytes_read--;
        -:  387:		}
    #####:  388:	      memmove (buf, p, bytes_read);
        -:  389:	    }
       10:  390:	  prev = bytes_read;
        -:  391:# endif
        -:  392:	}
       12:  393:      if (linepos > linelength)
branch  0 taken 83% (fallthrough)
branch  1 taken 17%
       10:  394:	linelength = linepos;
       12:  395:      words += in_word;
        -:  396:    }
        -:  397:#endif
        -:  398:  else
        -:  399:    {
    #####:  400:      bool in_word = false;
    #####:  401:      uintmax_t linepos = 0;
        -:  402:
    #####:  403:      while ((bytes_read = safe_read (fd, buf, BUFFER_SIZE)) > 0)
call    0 never executed
branch  1 never executed
branch  2 never executed
        -:  404:	{
    #####:  405:	  const char *p = buf;
    #####:  406:	  if (bytes_read == SAFE_READ_ERROR)
branch  0 never executed
branch  1 never executed
        -:  407:	    {
    #####:  408:	      error (0, errno, "%s", file);
call    0 never executed
    #####:  409:	      ok = false;
    #####:  410:	      break;
        -:  411:	    }
        -:  412:
    #####:  413:	  bytes += bytes_read;
        -:  414:	  do
        -:  415:	    {
    #####:  416:	      switch (*p++)
branch  0 never executed
branch  1 never executed
branch  2 never executed
branch  3 never executed
branch  4 never executed
branch  5 never executed
        -:  417:		{
    #####:  418:		case '\n':
    #####:  419:		  lines++;
        -:  420:		  /* Fall through. */
    #####:  421:		case '\r':
        -:  422:		case '\f':
    #####:  423:		  if (linepos > linelength)
branch  0 never executed
branch  1 never executed
    #####:  424:		    linelength = linepos;
    #####:  425:		  linepos = 0;
    #####:  426:		  goto word_separator;
    #####:  427:		case '\t':
    #####:  428:		  linepos += 8 - (linepos % 8);
    #####:  429:		  goto word_separator;
    #####:  430:		case ' ':
    #####:  431:		  linepos++;
        -:  432:		  /* Fall through. */
        -:  433:		case '\v':
    #####:  434:		word_separator:
    #####:  435:		  words += in_word;
    #####:  436:		  in_word = false;
    #####:  437:		  break;
    #####:  438:		default:
    #####:  439:		  if (isprint (to_uchar (p[-1])))
call    0 never executed
branch  1 never executed
branch  2 never executed
        -:  440:		    {
    #####:  441:		      linepos++;
    #####:  442:		      if (isspace (to_uchar (p[-1])))
call    0 never executed
branch  1 never executed
branch  2 never executed
    #####:  443:			goto word_separator;
    #####:  444:		      in_word = true;
        -:  445:		    }
    #####:  446:		  break;
        -:  447:		}
        -:  448:	    }
    #####:  449:	  while (--bytes_read);
branch  0 never executed
branch  1 never executed
        -:  450:	}
    #####:  451:      if (linepos > linelength)
branch  0 never executed
branch  1 never executed
    #####:  452:	linelength = linepos;
    #####:  453:      words += in_word;
        -:  454:    }
        -:  455:
       13:  456:  if (count_chars < print_chars)
branch  0 taken 0% (fallthrough)
branch  1 taken 100%
    #####:  457:    chars = bytes;
        -:  458:
       13:  459:  write_counts (lines, words, chars, bytes, linelength, file_x);
call    0 returned 100%
       13:  460:  total_lines += lines;
       13:  461:  total_words += words;
       13:  462:  total_chars += chars;
       13:  463:  total_bytes += bytes;
       13:  464:  if (linelength > max_line_length)
branch  0 taken 77% (fallthrough)
branch  1 taken 23%
       10:  465:    max_line_length = linelength;
        -:  466:
       13:  467:  return ok;
        -:  468:}
        -:  469:
        -:  470:static bool
function wc_file called 18 returned 100% blocks executed 87%
       18:  471:wc_file (char const *file, struct fstatus *fstatus)
        -:  472:{
       18:  473:  if (! file || STREQ (file, "-"))
branch  0 taken 56% (fallthrough)
branch  1 taken 44%
branch  2 taken 30% (fallthrough)
branch  3 taken 70%
        -:  474:    {
       11:  475:      have_read_stdin = true;
        -:  476:      if (O_BINARY && ! isatty (STDIN_FILENO))
        -:  477:	freopen (NULL, "rb", stdin);
       11:  478:      return wc (STDIN_FILENO, file, fstatus);
call    0 returned 100%
        -:  479:    }
        -:  480:  else
        -:  481:    {
        7:  482:      int fd = open (file, O_RDONLY | O_BINARY);
call    0 returned 100%
        7:  483:      if (fd == -1)
branch  0 taken 71% (fallthrough)
branch  1 taken 29%
        -:  484:	{
        5:  485:	  error (0, errno, "%s", file);
call    0 returned 100%
        5:  486:	  return false;
        -:  487:	}
        -:  488:      else
        -:  489:	{
        2:  490:	  bool ok = wc (fd, file, fstatus);
call    0 returned 100%
        2:  491:	  if (close (fd) != 0)
call    0 returned 100%
branch  1 taken 0% (fallthrough)
branch  2 taken 100%
        -:  492:	    {
    #####:  493:	      error (0, errno, "%s", file);
call    0 never executed
    #####:  494:	      return false;
        -:  495:	    }
        2:  496:	  return ok;
        -:  497:	}
        -:  498:    }
        -:  499:}
        -:  500:
        -:  501:/* Return the file status for the NFILES files addressed by FILE.
        -:  502:   Optimize the case where only one number is printed, for just one
        -:  503:   file; in that case we can use a print width of 1, so we don't need
        -:  504:   to stat the file.  */
        -:  505:
        -:  506:static struct fstatus *
function get_input_fstatus called 17 returned 100% blocks executed 100%
       17:  507:get_input_fstatus (int nfiles, char * const *file)
        -:  508:{
       17:  509:  struct fstatus *fstatus = xnmalloc (nfiles, sizeof *fstatus);
call    0 returned 100%
        -:  510:
       17:  511:  if (nfiles == 1
branch  0 taken 94% (fallthrough)
branch  1 taken 6%
       32:  512:      && ((print_lines + print_words + print_chars
branch  0 taken 6% (fallthrough)
branch  1 taken 94%
       16:  513:	   + print_bytes + print_linelength)
        -:  514:	  == 1))
        1:  515:    fstatus[0].failed = 1;
        -:  516:  else
        -:  517:    {
        -:  518:      int i;
        -:  519:
       33:  520:      for (i = 0; i < nfiles; i++)
branch  0 taken 52%
branch  1 taken 48% (fallthrough)
       44:  521:	fstatus[i].failed = (! file[i] || STREQ (file[i], "-")
branch  0 taken 30% (fallthrough)
branch  1 taken 70%
       10:  522:			     ? fstat (STDIN_FILENO, &fstatus[i].st)
       27:  523:			     : stat (file[i], &fstatus[i].st));
branch  0 taken 59% (fallthrough)
branch  1 taken 41%
call    2 returned 100%
call    3 returned 100%