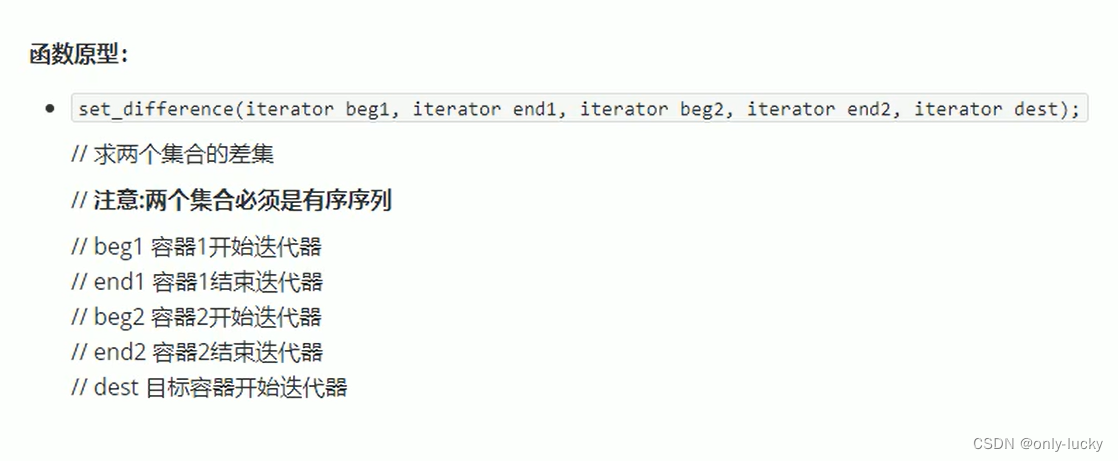
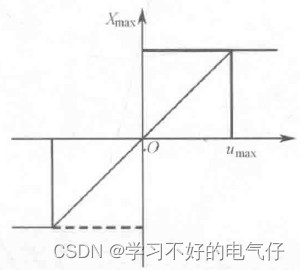
积分饱和现象
所谓积分饱和现象是指若系统存在一个方向的偏差,PID 控制器的输出由于积分作用的不断累加而加大,从而导致执行机构达到极限位置Xmax(例如阀门开度达到最大),如图所示,若控制器输出u(k)继续
增大,阀门开度不可能再增大,此时就称计算机输出控制量超出了正常运行范围而进入了饱和区。一旦系统出现反向偏差,u(k)逐渐从饱和区退出。进入饱和区越深则退出饱和区所需时间越长。在这段时间内,执行机构仍停留在极限位置而不能随偏差反向立即做出相应的改变,这时系统就像失去控制一样,造成控制性能恶化。这种现象称为积分饱和现象或积分失控现象。
抗积分饱和算法
作为防止积分饱和的方法之一就是抗积分饱和法。该方法的思路是在计算u(k)时,首先判断上一时刻的控制量u(k-1)是否已超出限制范围:
若u(k-1)> umax ,则只累加负偏差;若u(k-l)<umax,则只累加正偏差。这种算法可以避免控制量长时间停留在饱和区。
实例:
控制对象为:
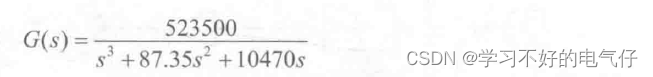
采样时间为 lms,取指令信号yd(k)=30,M=1,采用抗积分饱和算法进行离散系统阶跃响应,仿真结果如图1所示。取M=2,采用普通PID算法进行离散系统阶跃响应,其阶跃响应结果如图2所示。由仿真结果可以看出,采用抗积分饱和PID方法,可以避免控制量长时间停留在饱和区,防止系统产生超调。
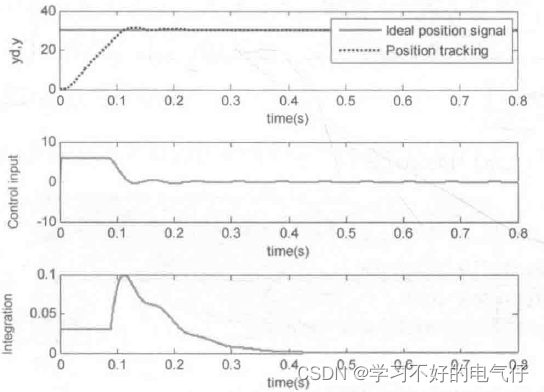
图1 抗积分饱和仿真结果(M=1)
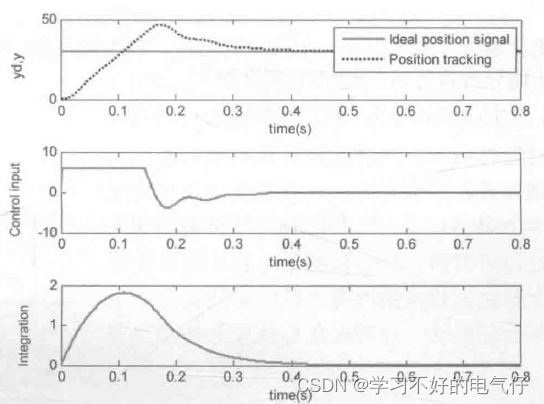
图2 普通PID算法进行离散系统阶跃响应结果(M=2)
仿真程序:
clear all;
close all;
ts=0.001;
syS=tf(5.235e005,[1.87.35,1.047e004,0];
dsys=c2d(sys,ts,'z);
[num,den]=tfdata(dsys,'v):
u1=0.0;u_2=0.0;u_ 3=0.0;
y _1=0;y_2=0;y_3=0;
x=[0,0,0];
error_1=0;
um=6;
kp=0.85;ki=9.0;kd=0.0;
for k=1:1:800
time(k)k *ts;
yd(k)=30; %Step Signal
u(k)=kp*x(1)+kd*x(2)+ki*x(3); %PID Controller
if u(k)>=um
Mu(k)=um;
end
if u(k)<=-um
u(k)=-um;
end
%Linear model
y(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(2)*u_l+num(3)*u_2+num(4)*u_3;
error(k)=yd(k)-y(k);
M=2;
ifM==1 %Using intergration sturation
if u(k)>-um
if error(k)>0
alpha=0;
else
alpha=1;
end
elseif u(k)<=-um
if error(k)>0
alpha=1;
else
alpha=0;
end
else
alpha=l;
end
else if M==2 %Not using intergration sturation
alpha=1;
end
%Return of PID parameters
u_3=u_2;u_2=u_1;u_1=u(k);
y_3=y_2;y_2=y_1;y_1=y(k);
error_l=error(k);
x(1)=error(k);
x(2)=(error(k)-error_1)ts;
x(3)=x(3)+alpha*error(k)*ts;
xi(k)=x(3);
end
figure(1);
subplot(311);
plot(time,yd,'r,time,y,'k:''linewidth',2);
xlabel('time(s)');ylabel('yd,y');
legend('ldeal position signal','Position tracking');
subplot(312);
plot(time,u,'r,linewidth' ,2);
xlabel('time(s)');ylabel('Control input');
subplot(313);
plot(time,xi,'r', linewidth',2);
xlabel('time(s)');ylabel('Integration');