得到新鲜甜甜圈的最多组数【LC1815】

有一个甜甜圈商店，每批次都烤 batchSize 个甜甜圈。这个店铺有个规则，就是在烤一批新的甜甜圈时，之前 所有 甜甜圈都必须已经全部销售完毕。给你一个整数 batchSize 和一个整数数组 groups ，数组中的每个整数都代表一批前来购买甜甜圈的顾客，其中 groups[i] 表示这一批顾客的人数。每一位顾客都恰好只要一个甜甜圈。

当有一批顾客来到商店时，他们所有人都必须在下一批顾客来之前购买完甜甜圈。如果一批顾客中第一位顾客得到的甜甜圈不是上一组剩下的，那么这一组人都会很开心。

你可以随意安排每批顾客到来的顺序。请你返回在此前提下，最多 有多少组人会感到开心。

一天不学习就又开始焦虑了 还是天天学习吧 今天的好难 respect灵神
祝大家兔年大吉钱兔无忧呀

• 思路

  • 首先，我们需要尽可能寻找$x$组顾客的数量之和为batchSize的倍数，那么下一组顾客一定会感到开心，以使开心的顾客总是最多【有点贪心】。
  • 比较容易写出的是一组顾客或者两组顾客的数量[两数之和]为batchSize的倍数。【计算过程中记录改组客人除以batchSize的余数，因为我们只关心是否是倍数，不关心数值的大小】
  • 由于batchSize最大值为9，因此这样计算之后，剩余没有配对的顾客，最多只有4种了，因此我们可以计算三数之和以及四数之和为batchSize的倍数的组数，如果计算完成后仍有顾客剩余，只有剩余的第一组顾客会满意，将结果+1返回即可【写不出来…】

• 思路：假设batchSize为$m$

  由于我们只关心上一批顾客购买后余下的甜甜圈数量，并且相同几组顾客到达的先后顺序不影响结果，因此存在重复子问题，可以用记忆化搜索最优的顾客顺序对应的分数，并使用状态压缩记录剩下顾客团体的个数以及上一批顾客购买后余下的甜甜圈数量，便于使用位运算进行状态的遍历及转移

  • 记忆化搜索过程

    • 当前操作：枚举$[0,n-1]$中$cnt[x]>0$的$x$，表示一批group[i] mod m = x 的顾客前来购买甜甜圈
    • 子问题、哪些操作会影响数据：余下的甜甜圈数量 $left$，以及剩余可以选的元素个数 $cnt[x]$【dfs函数的两个参数->使用状态压缩至一个int类型变量中】
    • 下一个子问题：那么$left$需要修改为$(left + x)%m $，并将$cnt[x]$减1。如果left=0时，下一批顾客会开心，结果加1

  • 状态压缩：使用int类型变量mask记录剩下顾客团体的个数以及上一批顾客购买后余下的甜甜圈数量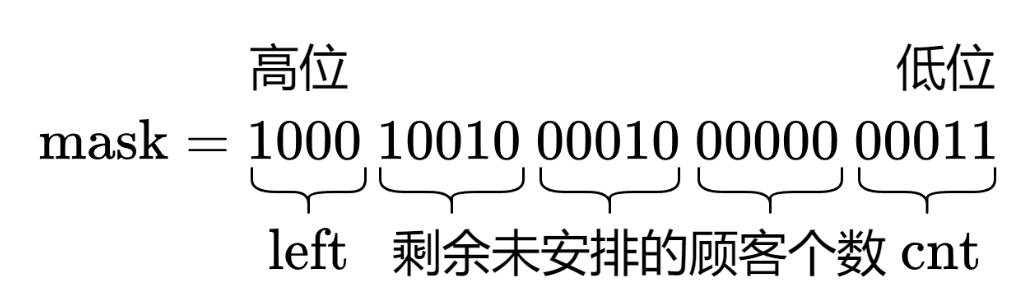

    

    • 由于剩下的顾客最多有4种，而$gruops[x]\le 30$，因此可以用5个比特表示顾客$x$的个数，一共需要20个比特，并使用$left$记录上一批顾客购买后剩下的甜甜圈数量，$left<9$，因此需要4个比特，因此可以使用int类型变量mask记录剩下顾客团体的个数以及上一批顾客购买后余下的甜甜圈数量

    • 使用int数组记录每个顾客团体对应的顾客数量val[i]，数组长度为$n$，val 越靠后的，在 mask 中的比特位越高

      比如val[0]对应mask中第0位至第4位，val[0]对应mask中第5位至第9位

  • 状态转移过程
    $$
    score=\left{
    \begin{aligned}
    1\qquad left=0 \
    0\qquad left !=0 \

    \end{aligned}
    \right.
    \
    dp[mask] = max {dp[mask],score + dfs[nextMask])}
    $$

• 实现

  首先遍历数组，记录单组顾客以及两组是$m$倍数的个数ans，然后使用状态压缩定义mask，记忆化搜索每个可能的状态对应的分数，并记录至map集合中，定义 $dfs(mask)$ 表示剩余顾客数量和left数量为mask时，往下进行操作能获得的最大分数，那么$ans+=dfs(mask)$ 即为最终结果

  • 由于数字过大，若使用数组会造成空间浪费，因此使用map集合，存储状态对应的分数
  • 位运算操作
    • 从mask中取出（高4位），记为left：mask<<20
    • 从mask中取出剩余顾客数量（低20位），记为msk：mask&((1<<20)-1)
    • 从msk中取出数量为val[i]对应的个数：msk>>(i*5)
    • 将left和msk组合在一起：left<<20|mask-(1<<j)

  class Solution {
      private int m;
      private int[] val;
      private final Map<Integer, Integer> cache = new HashMap<>();
  
      public int maxHappyGroups(int batchSize, int[] groups) {
          m = batchSize;
          int ans = 0;
          int[] cnt = new int[m];
          // 秒啊 一次遍历解决
          for (int x : groups) {
              x %= m;
              if (x == 0) ++ans; // 直接排在最前面
              else if (cnt[m - x] > 0) {
                  --cnt[m - x]; // 配对：两组顾客的和为batchSize的倍数
                  ++ans;
              } else ++cnt[x];
          }
  		// 剩下的顾客最多有4种 统计并记录剩余顾客种类以及对应组数
          int mask = 0, n = 0;
          for (int c : cnt) if (c > 0) ++n;
          val = new int[n];// 从大到小
          for (int x = 1; x < m; ++x)
              if (cnt[x] > 0) {
                  val[--n] = x; // val 越靠后的，在 mask 中的比特位越高
                  mask = mask << 5 | cnt[x];
              }
  
          return ans + dfs(mask);
      }
  
      private int dfs(int mask) {
          if (cache.containsKey(mask)) return cache.get(mask);
          int res = 0, left = mask >> 20, msk = mask & ((1 << 20) - 1);
          for (int i = 0, j = 0; i < val.length; ++i, j += 5) // 枚举顾客
              if ((msk >> j & 31) > 0) // cnt[val[i]] > 0
                  res = Math.max(res, (left == 0 ? 1 : 0) + dfs((left + val[i]) % m << 20 | msk - (1 << j)));
          cache.put(mask, res);
          return res;
      }
  }
  
  作者：灵茶山艾府
  链接：https://leetcode.cn/problems/maximum-number-of-groups-getting-fresh-donuts/solutions/2072545/by-endlesscheng-r5ve/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  • 复杂度
    • 时间复杂度：$O(m^2(\frac{n}{m}{)}^{m/2})$，$n$为数组的长度，$m$为batchSize，最坏情况下没有两个一对的，例如 groups 中只有 [1,4] 中的数。根据基本不等式，把 30 平分成 8+8+7+7 是最优的，那么至多有 9×(8×8×7×7)=28224 个状态，每个状态执行至多 4次循环，因此记忆化搜索的计算量至多为 28224×4=112896
    • 空间复杂度：$O(m(\frac{n}{m}{)}^{m/2})$，主要取决于状态个数