入门小菜鸟,希望像做笔记记录自己学的东西,也希望能帮助到同样入门的人,更希望大佬们帮忙纠错啦~侵权立删。
✨完整代码在我的github上,有需要的朋友可以康康✨
https://github.com/tt-s-t/Deep-Learning.git
目录
一、背景
二、原理
1、前向传播
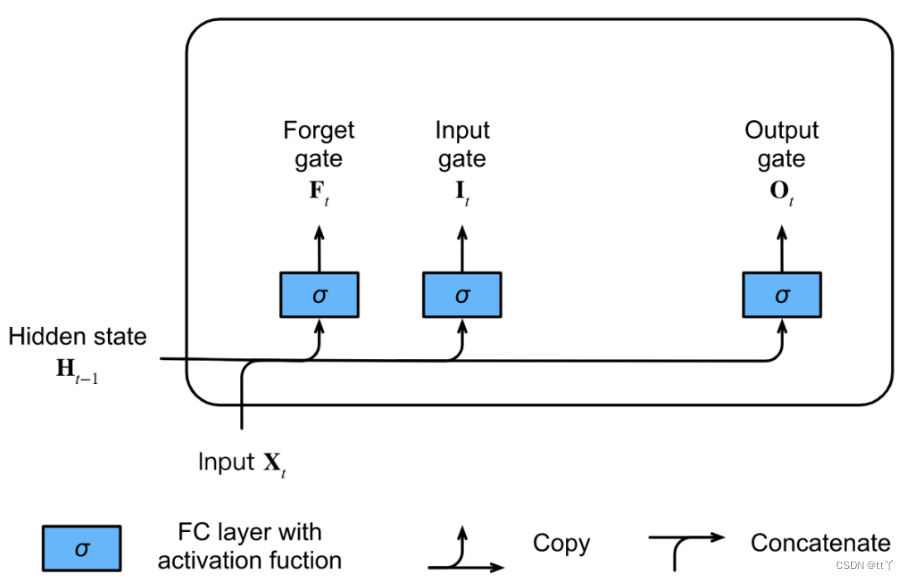
(1)输入门、遗忘门和输出门
(2)候选记忆细胞
(3)记忆细胞
(4)隐藏状态
(5)输出
2、反向传播
(1)输出层参数
(2)过渡
(3)候选记忆细胞的参数
(4)输出门的参数
(5)遗忘门的参数
(6)输入门的参数
(7)上一隐藏状态and记忆细胞
三、总结
四、LSTM的优缺点
1、优点
2、缺点
五、LSTM代码实现
1、numpy实现LSTM类
(1)前期准备
(2)初始化参数
(3)前向传播
(4)反向传播
(5)预测
2、调用我们实现的LSTM进行训练与预测
3、结果
一、背景
当时间步数(T)较大或时间步(t)较小的时候,RNN的梯度较容易出现衰减或爆炸。虽然裁剪梯度可以应对梯度爆炸,但是无法解决梯度衰减的问题。这个原因使得RNN在实际中难以捕捉时间序列中时间步(t)距离较大的依赖关系。因此LSTM应运而生。
RNN详解可以看看:RNN循环神经网络_tt丫的博客-CSDN博客_rnn应用领域
二、原理
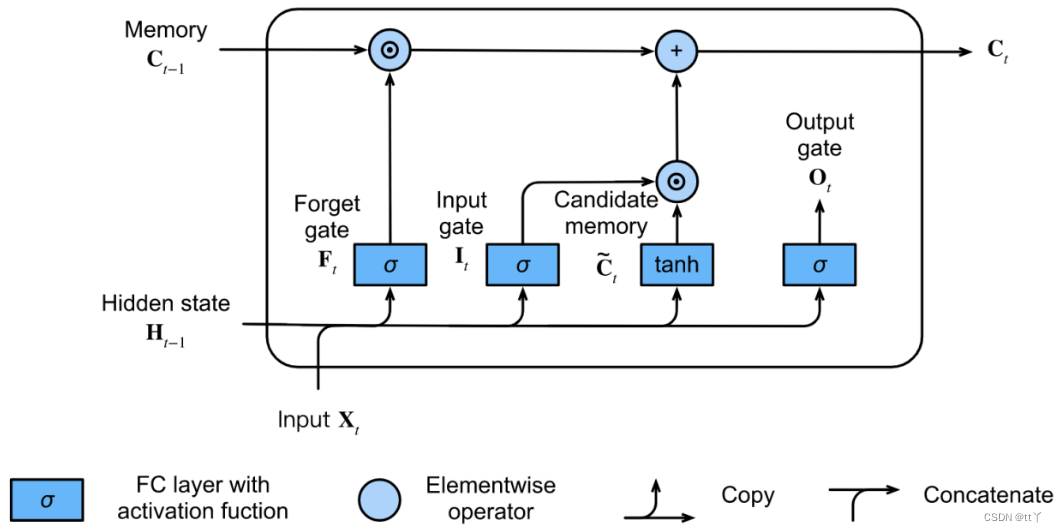
1、前向传播
输入:当前时间步的输入与上一时间步隐藏状态
(1)输入门、遗忘门和输出门
输入门:
遗忘门:
输出门:
他们都在后面起到一个比例调节的作用。
其中,
,
为激活函数(sigmoid函数),故取值范围为:[0,1]
n为样本数,d为输入的特征数,h为隐藏大小。
(2)候选记忆细胞
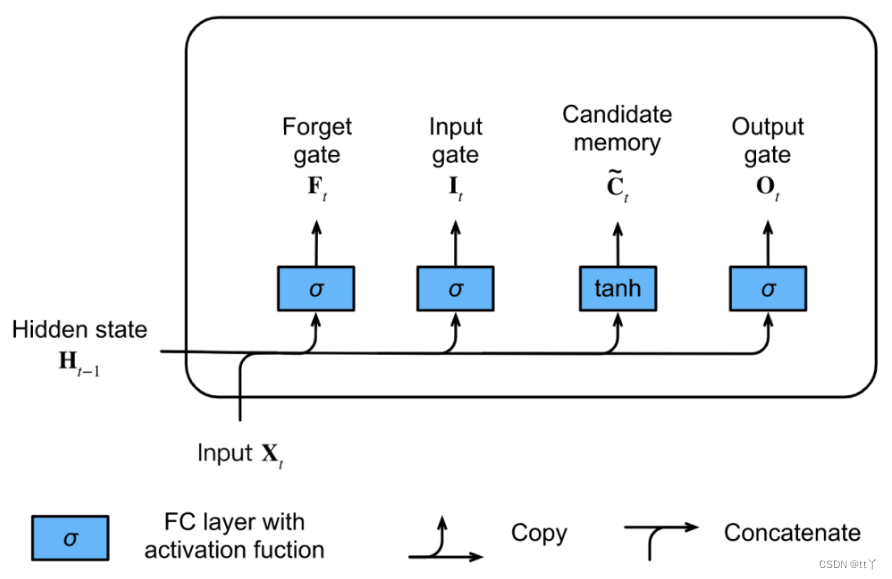
(3)记忆细胞
当前时间步记忆细胞的计算组合了上一时间步记忆细胞和当前时间步候选记忆细胞的信息。
遗忘门控制上一时间步的记忆细胞
中的信息是否传递到当前时间步的记忆细胞,而输出门
则控制当前时间步的输入
通过候选记忆细胞的
如何流入当前时间步的记忆细胞。
如果遗忘门一直近似为1且输入门一直近似为0,则说明:过去的记忆细胞将一直通过时间保存并传递到当前时间步,而当前输入则被屏蔽掉。
这个设计可以应对循环神经网络中的梯度衰减问题(可以有选择地对前面的信息进行保留,不至于直接出现指数项),并更好地捕捉时间序列中时间步距离较大的依赖关系(存在中)。
(4)隐藏状态
我们通过输出门来控制从记忆细胞到隐藏状态
的信息流动。
当输出门近似为1时,记忆细胞信息将传递到隐藏状态供输出层使用;近似为0时,记忆细胞信息只自己保留。
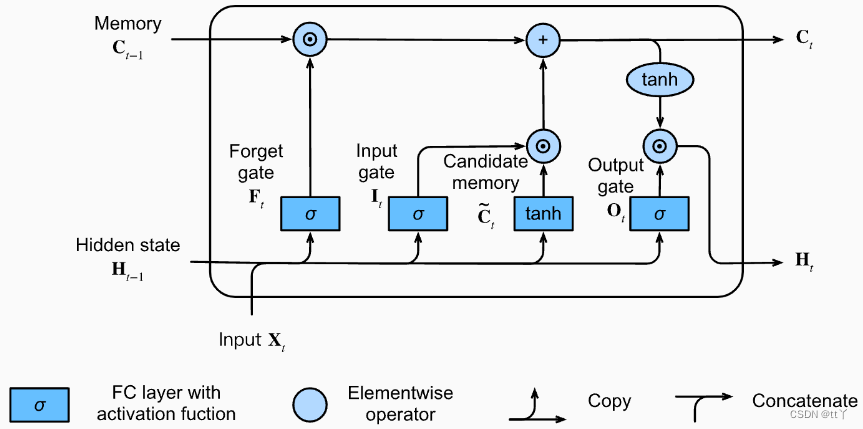
(5)输出
2、反向传播
已知(注:*是矩阵乘法,•是矩阵上对应元素相乘)
(1)输出层参数
Note:这里的指的是上一次(即t+1时间步)计算得到的
;
;
(2)过渡
对于链式法则涉及到记忆细胞的,我们设为
Note:同样的,这里的
指的是上一次(即t+1时间步)计算得到的
对于链式法则涉及到候选记忆细胞的,我们设为
对于链式法则涉及到输出门的,我们设为
对于链式法则涉及到遗忘门的,我们设为
对于链式法则涉及到输入门的,我们设为
(3)候选记忆细胞的参数
;
;
(4)输出门的参数
;
;
(5)遗忘门的参数
;
;
(6)输入门的参数
;
;
(7)上一隐藏状态and记忆细胞
三、总结
LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径,让信息能在序列连中传递下去——即网络的“记忆”。理论上讲,细胞状态能够将序列处理过程中的相关信息一直传递下去。
因此,即使是较早时间步的信息也能携带到较后时间步的细胞中来,这克服了短时记忆的影响(RNN可能会因为指数项的累积,变得越来越小或大到“面目全非”,LSTM将累积下来的影响由指数运算转化为了加法运算与参数学习控制去留)。信息的添加和移除我们通过“门”结构来实现,“门”结构在训练过程中会去学习该保存或遗忘哪些信息。
每个门起到的作用顾名思义:
遗忘门:决定什么信息需要从记忆细胞中删除——0:将
(过去的记忆)的值删除,1:保留
的值;
输入门:决定输入的哪些新信息(输入信息通过候选记忆细胞传入)需要增加至记忆细胞中;
输出门:决定从记忆细胞中选出哪些信息进行输出。
四、LSTM的优缺点
1、优点
继承了大部分RNN模型的特性,同时解决了梯度反传过程由于逐步缩减而产生的梯度衰减问题,使用门控与记忆细胞来学习如何取舍过去的信息,如何提取当前的输入信息。
具体改进点:RNN这部分的取舍过去信息和提取当前输入信息都是由参数学习得到的(权重参数),结构过于简单,原理也上也有所欠缺(一般我们判断过去信息对现在重不重要也是需要根据过去信息以及当前状态同时决定的,而非直接由一个U和W权重矩阵决定)
2、缺点
(1)并行处理上存在劣势,难以落地;
(2)RNN的梯度问题在LSTM及其变种里面得到了一定程度的解决,但还是不够。它可以处理100个量级的序列,而对于1000个量级,或者更长的序列则依然会很棘手;
(3)模型结构复杂,计算费时。每一个LSTM的cell里面都意味着有4个全连接层(MLP),如果LSTM的时间跨度很大,并且网络又很深,这个计算量会很大,很耗时。
五、LSTM代码实现
这里只展示我用numpy搭建的LSTM网络,并且实现对“abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz”序列数据的预测。详细地可以在我的github的LSTM文件夹上看,包括用pytorch实现的LSTM实现文本生成,以及这个numpy搭建的LSTM实现对序列数据预测的完整版本。
http://https://github.com/tt-s-t/Deep-Learning.git
首先我们定义一个LSTM类。
1、numpy实现LSTM类
(1)前期准备
import numpy as np
def sigmoid(x):
x_ravel = x.ravel() # 将numpy数组展平
length = len(x_ravel)
y = []
for index in range(length):
if x_ravel[index] >= 0:
y.append(1.0 / (1 + np.exp(-x_ravel[index])))
else:
y.append(np.exp(x_ravel[index]) / (np.exp(x_ravel[index]) + 1))
return np.array(y).reshape(x.shape)
def tanh(x):
result = (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
return result(2)初始化参数
class LSTM(object):
def __init__(self, input_size, hidden_size):
self.input_size = input_size
self.hidden_size = hidden_size
#输入门
self.Wxi = np.random.randn(input_size, hidden_size)
self.Whi = np.random.randn(hidden_size, hidden_size)
self.B_i = np.zeros((1, hidden_size))
#遗忘门
self.Wxf = np.random.randn(input_size, hidden_size)
self.Whf = np.random.randn(hidden_size, hidden_size)
self.B_f = np.zeros((1, hidden_size))
#输出门
self.Wxo = np.random.randn(input_size, hidden_size)
self.Who = np.random.randn(hidden_size, hidden_size)
self.B_o = np.zeros((1, hidden_size))
#候选记忆细胞
self.Wxc = np.random.randn(input_size, hidden_size)
self.Whc = np.random.randn(hidden_size, hidden_size)
self.B_c = np.zeros((1, hidden_size))
#输出
self.W_hd = np.random.randn(hidden_size, input_size)
self.B_d = np.zeros((1, input_size))(3)前向传播
def forward(self,X,Ht_1,Ct_1): #前向传播
#存储
self.it_stack = {} #输入门存储
self.ft_stack = {} #遗忘门存储
self.ot_stack = {} #输出门存储
self.cc_stack = {} #候选记忆细胞存储
self.c_stack = {} #记忆细胞存储
self.X_stack = {} #X存储
self.Ht_stack = {} #隐藏状态存储
self.Y_stack = {} #输出存储
self.Ht_stack[-1] = Ht_1
self.c_stack[-1] = Ct_1
self.T = X.shape[0]
for t in range(self.T):
self.X_stack[t] = X[t].reshape(-1,1).T
#输入门
net_i = np.matmul(self.X_stack[t], self.Wxi) + np.matmul(self.Ht_stack[t-1], self.Whi) + self.B_i
it = sigmoid(net_i)
self.it_stack[t] = it
#遗忘门
net_f = np.matmul(self.X_stack[t], self.Wxf) + np.matmul(self.Ht_stack[t-1], self.Whf) + self.B_f
ft = sigmoid(net_f)
self.ft_stack[t] = ft
#输出门
net_o = np.matmul(self.X_stack[t], self.Wxo) + np.matmul(self.Ht_stack[t-1], self.Who) + self.B_o
ot = sigmoid(net_o)
self.ot_stack[t] = ot
#候选记忆细胞
net_cc = np.matmul(self.X_stack[t], self.Wxc) + np.matmul(self.Ht_stack[t-1], self.Whc) + self.B_c
cct = tanh(net_cc)
self.cc_stack[t] = cct
#记忆细胞
Ct = ft*self.c_stack[t-1]+it*cct
self.c_stack[t] = Ct
#隐藏状态
Ht = ot*tanh(Ct)
self.Ht_stack[t] = Ht
#输出
y = np.matmul(Ht, self.W_hd) + self.B_d
Yt = np.exp(y) / np.sum(np.exp(y)) #softmax
self.Y_stack[t] = Yt(4)反向传播
def backward(self,target,lr):
#初始化
dH_1, dnet_ct_1 = np.zeros([1,self.hidden_size]), np.zeros([1,self.hidden_size])
dWxi, dWhi, dBi = np.zeros_like(self.Wxi), np.zeros_like(self.Whi), np.zeros_like(self.B_i)
dWxf, dWhf, dBf = np.zeros_like(self.Wxf), np.zeros_like(self.Whf), np.zeros_like(self.B_f)
dWxo, dWho, dBo = np.zeros_like(self.Wxo), np.zeros_like(self.Who), np.zeros_like(self.B_o)
dWxc, dWhc, dBc = np.zeros_like(self.Wxc), np.zeros_like(self.Whc), np.zeros_like(self.B_c)
dWhd,dBd = np.zeros_like(self.W_hd),np.zeros_like(self.B_d)
self.loss = 0
for t in reversed(range(self.T)): #反过来开始,越往前面分支越多
dY = self.Y_stack[t] - target[t].reshape(-1,1).T
self.loss += -np.sum(np.log(self.Y_stack[t]) * target[t].reshape(-1,1).T)
#对输出的参数
dWhd += np.matmul(self.Ht_stack[t].T,dY)
dBd += dY
dH = np.matmul(dY, self.W_hd.T) + dH_1 #dH更新
#对有关输入门,遗忘门,输出门,候选记忆细胞中参数的求导的共同点
temp = tanh(self.c_stack[t])
dnet_ct = dH * self.ot_stack[t] * (1-temp*temp) + dnet_ct_1 #记忆细胞
dnet_cct = dnet_ct * self.it_stack[t] * (1 - self.cc_stack[t]*self.cc_stack[t]) #候选记忆细胞
dnet_o = dH * temp * self.ot_stack[t] * (1 - self.ot_stack[t]) #输出门
dnet_f = dnet_ct * self.c_stack[t-1] * self.ft_stack[t] * (1 - self.ft_stack[t]) #遗忘门
dnet_i = dnet_ct * self.cc_stack[t] * self.it_stack[t] * (1 - self.it_stack[t]) #输入门
#候选记忆细胞中参数
dWxc += np.matmul(self.X_stack[t].T, dnet_cct)
dWhc += np.matmul(self.Ht_stack[t-1].T, dnet_cct)
dBc += dnet_cct
#输出门
dWxo += np.matmul(self.X_stack[t].T, dnet_o)
dWho += np.matmul(self.Ht_stack[t-1].T, dnet_o)
dBo += dnet_o
#遗忘门
dWxf += np.matmul(self.X_stack[t].T, dnet_f)
dWhf += np.matmul(self.Ht_stack[t-1].T, dnet_f)
dBf += dnet_f
#输入门
dWxi += np.matmul(self.X_stack[t].T, dnet_i)
dWhi += np.matmul(self.Ht_stack[t-1].T, dnet_i)
dBi += dnet_i
#Ht-1和Ct-1
dH_1 = np.matmul(dnet_cct, self.Whc) + np.matmul(dnet_i, self.Whi) + np.matmul(dnet_f, self.Whf) + np.matmul(dnet_o, self.Who)
dnet_ct_1 = dnet_ct * self.ft_stack[t]
#候选记忆细胞
self.Wxc += -lr * dWxc
self.Whc += -lr * dWhc
self.B_c += -lr * dBc
#输出门
self.Wxo += -lr * dWxo
self.Who += -lr * dWho
self.B_o += -lr * dBo
#遗忘门
self.Wxf += -lr * dWxf
self.Whf += -lr * dWhf
self.B_f += -lr * dBf
#输入门
self.Wxi += -lr * dWxi
self.Whi += -lr * dWhi
self.B_i += -lr * dBi
return self.loss(5)预测
def pre(self,input_onehot,h_prev,c_prev,next_len,vocab): #input_onehot为输入的一个词的onehot编码,next_len为需要生成的单词长度,vocab是"索引-词"的词典
xs, hs, cs = {}, {}, {} #字典形式存储
hs[-1] = np.copy(h_prev) #隐藏状态赋予
cs[-1] = np.copy(c_prev)
xs[0] = input_onehot
pre_vocab = []
for t in range(next_len):
#输入门
net_i = np.matmul(xs[t], self.Wxi) + np.matmul(hs[t-1], self.Whi) + self.B_i
it = sigmoid(net_i)
#遗忘门
net_f = np.matmul(xs[t], self.Wxf) + np.matmul(hs[t-1], self.Whf) + self.B_f
ft = sigmoid(net_f)
#输出门
net_o = np.matmul(xs[t], self.Wxo) + np.matmul(hs[t-1], self.Who) + self.B_o
ot = sigmoid(net_o)
#候选记忆细胞
net_cc = np.matmul(xs[t], self.Wxc) + np.matmul(hs[t-1], self.Whc) + self.B_c
cct = tanh(net_cc)
#记忆细胞
Ct = ft*cs[t-1]+it*cct
cs[t] = Ct
#隐藏状态
Ht = ot*tanh(Ct)
hs[t] = Ht
#输出
Ot = np.matmul(Ht, self.W_hd) + self.B_d
Yt = np.exp(Ot) / np.sum(np.exp(Ot)) #softmax
pre_vocab.append(vocab[np.argmax(Yt)])
xs[t+1] = np.zeros((1, self.input_size)) # init
xs[t+1][0,np.argmax(Yt)] = 1
return pre_vocab2、调用我们实现的LSTM进行训练与预测
from lstm_model import LSTM
import numpy as np
import math
class Dataset(object):
def __init__(self,txt_data, sequence_length):
self.txt_len = len(txt_data) #文本长度
vocab = list(set(txt_data)) #所有字符合集
self.n_vocab = len(vocab) #字典长度
self.sequence_length = sequence_length
self.vocab_to_index = dict((c, i) for i, c in enumerate(vocab)) #词-索引字典
self.index_to_vocab = dict((i, c) for i, c in enumerate(vocab)) #索引-词字典
self.txt_index = [self.vocab_to_index[i] for i in txt_data] #输入文本的索引表示
def one_hot(self,input):
onehot_encoded = []
for i in input:
letter = [0 for _ in range(self.n_vocab)]
letter[i] = 1
onehot_encoded.append(letter)
onehot_encoded = np.array(onehot_encoded)
return onehot_encoded
def __getitem__(self, index):
return (
self.txt_index[index:index+self.sequence_length],
self.txt_index[index+1:index+self.sequence_length+1]
)
#输入的有规律的序列数据
#txt_data = "abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc abc"
txt_data = "abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz abcdefghijklmnopqrstuvwxyz "
#config
max_epoch = 5000
sequence_length = 28
dataset = Dataset(txt_data,sequence_length)
batch_num = math.ceil(dataset.txt_len /sequence_length) #向上取整
hidden_size = 32
lr = 1e-3
model = LSTM(dataset.n_vocab,hidden_size)
#训练
for epoch in range(max_epoch):
h_prev = np.zeros((1, hidden_size))
c_prev = np.zeros((1, hidden_size))
loss = 0
for b in range(batch_num):
(x,y) = dataset[b]
input = dataset.one_hot(x)
target = dataset.one_hot(y)
ps = model.forward(input,h_prev,c_prev) #注意:每个batch的h都是从0初始化开始,batch与batch间的隐藏状态没有关系
loss += model.backward(target,lr)
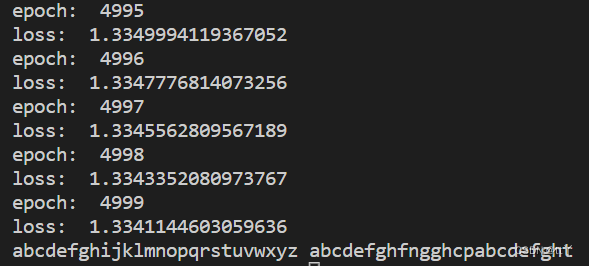
print("epoch: ",epoch)
print("loss: ",loss/batch_num)
#预测
input_txt = 'a'
input_onehot = dataset.one_hot([dataset.vocab_to_index[input_txt]])
next_len = 50 #预测后几个word
h_prev = np.zeros((1, hidden_size))
c_prev = np.zeros((1, hidden_size))
pre_vocab = ['a']
pre_vocab1 = model.pre(input_onehot,h_prev,c_prev,next_len,dataset.index_to_vocab)
pre_vocab = pre_vocab + pre_vocab1
print(''.join(pre_vocab))3、结果
以a开头预测后续的50个字符。
欢迎大家在评论区批评指正,谢谢~