前言

这篇文章将介绍数码管的显示其中包含了动态数码管和静态数码管两种。

一、数码管简介

数码管其实就是由多个发光二极管封装在一起组成“8”字型的器件当分别点亮这些发光二极管时就可以组成不同的数字显示出来。

二、数码管原理图

下图我们可以知道8个数码管通过了一个74HC245芯片和单片机的P01-P07相连接。
74HC138译码器通过P22-P24输出的相对于的电平选择控制哪个具体的数码管。
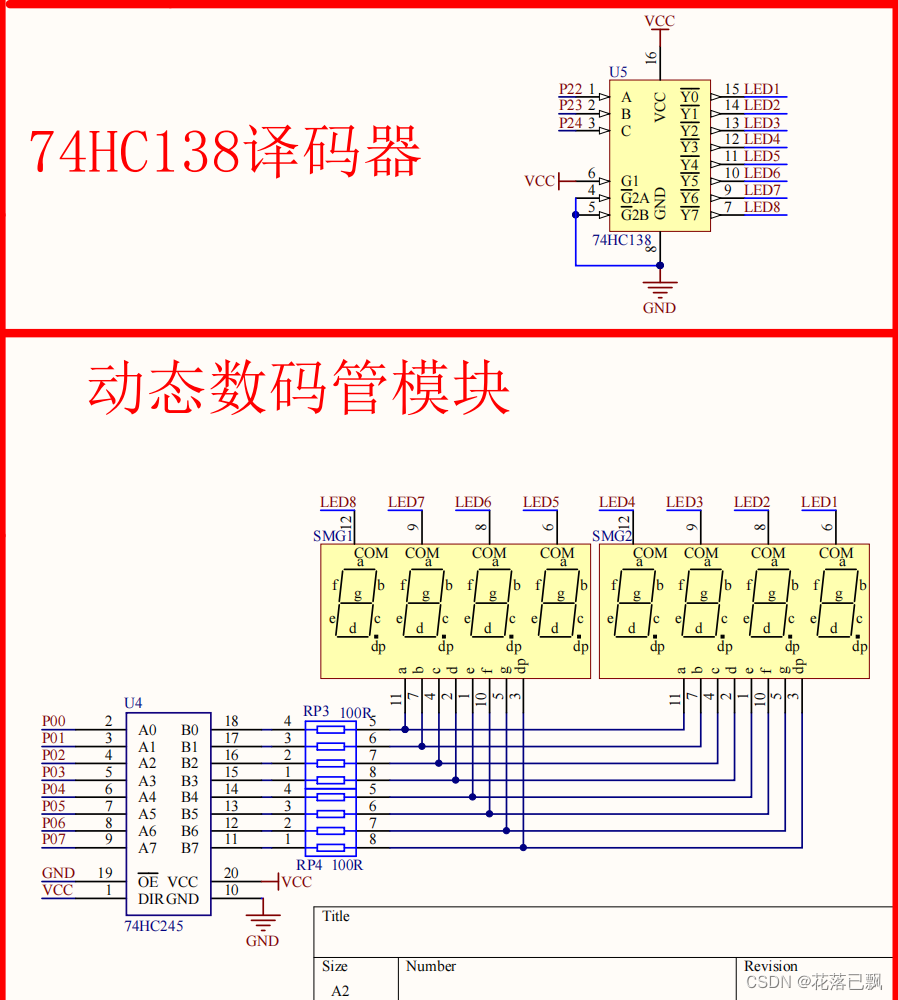
在这里插入图片描述
74HC138是一款高速CMOS器件，74HC138引脚兼容低功耗肖特基TTL（LSTTL）系列。74HC138译码器可接受3位二进制加权地址输入（A0, A1和A2），并当使能时，提供8个互斥的低有效输出（Y0至Y7）。
这样我们就可以只通过3个引脚就可以选择控制8个数码管了。
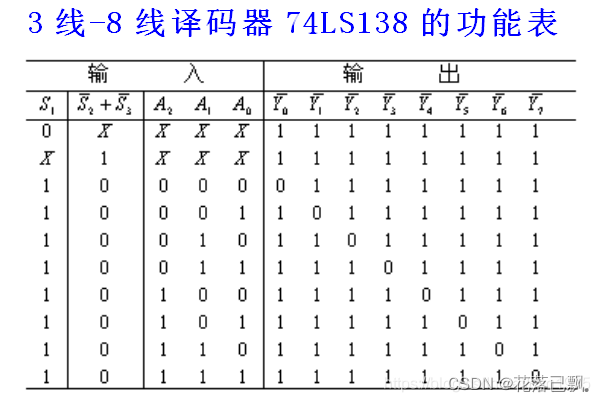
下面是74138译码器的真值表，当P22-P24都输出0时就选择了第一个数码管，P22为1时P23-P24输出0时选择第二个数码管，以此类推。看不懂的同学建议去看看数字电路的知识。
在这里插入图片描述

三、数码管显示原理

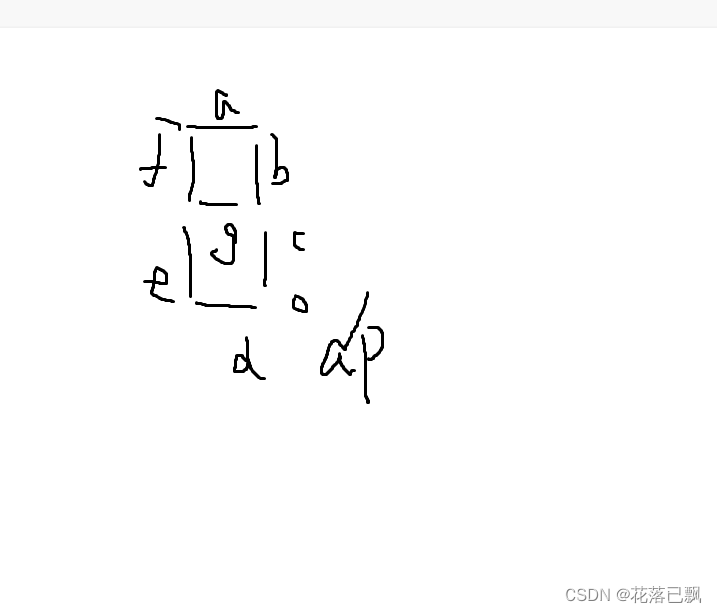
一个数码管就是由8个LED组成的想要实现对应的数字或者字母那么就去点亮对应的LED灯即可。
比如想要显示数字0那么就熄灭LED g和LED dp，其他的数码管都分别点亮起来这里就能得到想要显示的数字0。
这样的话我们能得到一个二进制数：0011 1111，这个二进制数就代表了熄灭LED g和LED dp，这里LED灯为高电平点亮。这个二进制数转为16进制数就是0x3f。
当要显示0时将0x3f赋值给P0即可。
P0 = 0x3f(显示数字0)
这个0x3f被称为段码，因为数码管就是由8个LED段组成的。
在这里插入图片描述
这里给出其他数字的段码显示：

//共阴极数码管显示0~F的段码数据
u8 gsmg_code[17]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,
				0x7f,0x6f,0x77,0x7c,0x39,0x5e,0x79,0x71};

四、静态数码管代表编写

#include <reg52.h>

//共阴极数码管显示0~F的段码数据
u8 gsmg_code[17]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,
				0x7f,0x6f,0x77,0x7c,0x39,0x5e,0x79,0x71};

void main()
{	
	P0=gsmg_code[0];//将数组第1个数据赋值给数码管段选口
					//显示数字0
	while(1)
	{
	   	
	}		
}

五、动态数码管

动态数码管的原理就是利用了人眼的识别比较弱识别不到数码管的快速变换而达到的。
代码实现：
我们在while1里面不断的去扫描这8个数码管将对应的数据显示到数码管上面，这样我们的人眼就认为数码管可以做到分别显示不同的数值了。

#include <reg52.h>

//共阴极数码管断码
unsigned char gsmg_code[17]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,
				0x7f,0x6f,0x77,0x7c,0x39,0x5e,0x79,0x71};
		

//定义数码管位选信号控制脚
//74138的三个输入引脚
sbit LSA=P2^2;
sbit LSB=P2^3;
sbit LSC=P2^4;
							
				
/*延时函数
单位:ms
x:延时的数值
*/
void delayms(unsigned int x)
{
   unsigned char i;
	 while(x--)
	 {
		 for(i=0;i<113;i++);
	 }
}
				
/*
数码管显示函数
pos:在第几位显示
dat:要显示的数据
*/
void select_display(unsigned char pos, unsigned char dat)
{
	  switch(pos)//位选(选择在第几个位置显示 原理参照74138的真值表)
		{
			case 0: LSC=1;LSB=1;LSA=1;break;
			case 1: LSC=1;LSB=1;LSA=0;break;
			case 2: LSC=1;LSB=0;LSA=1;break;
			case 3: LSC=1;LSB=0;LSA=0;break;
			case 4: LSC=0;LSB=1;LSA=1;break;
			case 5: LSC=0;LSB=1;LSA=0;break;
			case 6: LSC=0;LSB=0;LSA=1;break;
			case 7: LSC=0;LSB=0;LSA=0;break;
		}
		P0 = gsmg_code[dat];
		delayms(1);//等待数据显示稳定
		P0 = 0x00;//消影
}

void main()
{
	
	while(1)
	{
		select_display(0, 0);
		select_display(1, 1);
		select_display(2, 2);
		select_display(3, 3);
		select_display(4, 4);
		select_display(5, 5);
		select_display(6, 6);
		select_display(7, 7);
	}
}