Leetcode——第 329 场周赛

news2024/9/25 21:27:01

题目链接：

交替数字和
根据第 K 场考试的分数排序
执行逐位运算使字符串相等
拆分数组的最小代价

题目描述

交替数字和

给你一个正整数 n 。n中的每一位数字都会按下述规则分配一个符号：

最高有效位 上的数字分配到正号。
剩余每位上数字的符号都与其相邻数字相反。
返回所有数字及其对应符号的和。

示例 1：

输入：n = 521
输出：4
解释：(+5) + (-2) + (+1) = 4

示例 2：

输入：n = 111
输出：1
解释：(+1) + (-1) + (+1) = 1

示例 3：

输入：n = 886996
输出：0
解释：(+8) + (-8) + (+6) + (-9) + (+9) + (-6) = 0

提示：

$1 <= n <= 10^9$

分析：根据题意直接模拟即可。

时间复杂度： $O (n)$

代码：

class Solution {
public:
    int alternateDigitSum(int n) {
        string s = to_string(n);
        int ans = 0;
        //初始为整数，然后正负交替
        int f = 1;
        for(auto &c:s){
            ans += f * (c - '0');
            f *= -1;
        }
        return ans;
    }
};

根据第 K 场考试的分数排序

班里有 m位学生，共计划组织 n场考试。给你一个下标从 0开始、大小为 m x n的整数矩阵 score，其中每一行对应一位学生，而 score[i][j]表示第 i 位学生在第 j 场考试取得的分数。矩阵 score包含的整数 互不相同 。

另给你一个整数 k。请你按第 k场考试分数从高到低完成对这些学生（矩阵中的行）的排序。

返回排序后的矩阵。

示例 1：

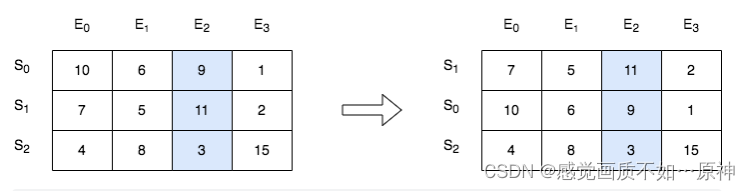
在这里插入图片描述

输入：score = [[10,6,9,1],[7,5,11,2],[4,8,3,15]], k = 2
输出：[[7,5,11,2],[10,6,9,1],[4,8,3,15]]
解释：在上图中，S 表示学生，E 表示考试。

下标为 1 的学生在第 2 场考试取得的分数为 11 ，这是考试的最高分，所以 TA 需要排在第一。
下标为 0 的学生在第 2 场考试取得的分数为 9 ，这是考试的第二高分，所以 TA 需要排在第二。
下标为 2 的学生在第 2 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第三。

示例 2：

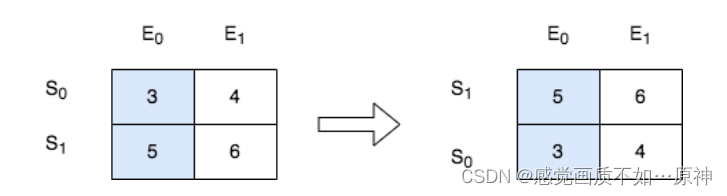
在这里插入图片描述

输入：score = [[3,4],[5,6]], k = 0
输出：[[5,6],[3,4]]
解释：在上图中，S 表示学生，E 表示考试。

下标为 1 的学生在第 0 场考试取得的分数为 5 ，这是考试的最高分，所以 TA 需要排在第一。
下标为 0 的学生在第 0 场考试取得的分数为 3 ，这是考试的最低分，所以 TA 需要排在第二。

提示：

$m == score . l e n g t h$
$n == score [i] . l e n g t h$
$1 <= m, n <= 250$
$1 <= score[i][j] <= 10^5$
score由不同的整数组成
$0 <= k < n$

分析：按照第 k 列，从大到小重排数组即可。

时间复杂度： $O (n l o g n)$

代码：

class Solution {
public:
    vector<vector<int>> sortTheStudents(vector<vector<int>>& score, int k) {
        sort(score.begin(),score.end(),[&](auto &a,auto &b){
            return a[k] > b[k];
        });

        return score;
    }
};

执行逐位运算使字符串相等

给你两个下标从 0 开始的二元字符串 s和 t，两个字符串的长度均为 n。你可以对 s执行下述操作任意次：

选择两个不同的下标 i和 j，其中 $0 <= i, j < n$ 。
同时，将 s[i] 替换为 (s[i] OR s[j]) ，s[j] 替换为 (s[i] XOR s[j]) 。

例如，如果 s = "0110"，你可以选择 $i = 0 和 j = 2$ ，然后同时将 s[0] 替换为 (s[0] OR s[2] = 0 OR 1 = 1)，并将 s[2] 替换为 (s[0] XOR s[2] = 0 XOR 1 = 1)，最终得到 s = “1110” 。

如果可以使 s等于 t，返回 true ，否则，返回 false 。

示例 1：

输入：s = “1010”, t = “0110”
输出：true 解释：可以执行下述操作：

选择 i = 2 和 j = 0 ，得到 s = “0010”.
选择 i = 2 和 j = 1 ，得到 s = “0110”. 可以使 s 等于 target ，返回 true 。

示例 2：

输入：s = “11”, t = “00”
输出：false
解释：执行任意次操作都无法使 s 等于 target 。

提示：

$n == s . l e n g t h == t a r g e t . l e n g t h$
$2 <= n <= 10^5$
s和 t仅由数字 0 和 1 组成

分析：

要么 s和 t同时都有 1，要么 s和 t全部都是 0。否则 s不能变为 t。

时间复杂度： $O (n)$

代码：

class Solution {
public:
    bool makeStringsEqual(string s, string t) {
        if(s == t) return true;
        int n = s.size();
        bool a = false,b = false;

        for(int i = 0;i < n;i++){
            if(s[i] == '1') a = true;
            if(t[i] == '1') b = true;
        }
        //要么都有1 要么都没有1 才成立
        return (a && b) || (!a && !b);
    }
};

拆分数组的最小代价

给你一个整数数组 nums和一个整数 k。

将数组拆分成一些非空子数组。拆分的代价是每个子数组中的 重要性 之和。

令 trimmed(subarray)作为子数组的一个特征，其中所有仅出现一次的数字将会被移除。

例如， $t r imm e d ([3, 1, 2, 4, 3, 4]) = [3, 4, 3, 4]$ 。
子数组的 重要性 定义为 $k + t r imm e d (s u ba rr a y) . l e n g t h$ 。

例如，如果一个子数组是 [1,2,3,3,3,4,4]， $t r imm e d ([1, 2, 3, 3, 3, 4, 4]) = [3, 3, 3, 4, 4]$ 。这个子数组的重要性就是 k + 5。

找出并返回拆分 nums的所有可行方案中的最小代价。

子数组 是数组的一个连续非空元素序列。

示例 1：

输入：nums = [1,2,1,2,1,3,3], k = 2
输出：8
解释：将 nums 拆分成两个子数组：[1,2],[1,2,1,3,3] [1,2] 的重要性是 2 + (0) = 2 。 [1,2,1,3,3] 的重要性是 2 + (2 + 2) = 6 。拆分的代价是 2 + 6 = 8 ，可以证明这是所有可行的拆分方案中的最小代价。

示例 2：

输入：nums = [1,2,1,2,1], k = 2
输出：6
解释：将 nums 拆分成两个子数组：[1,2], [1,2,1] 。
[1,2] 的重要性是 2 + (0) = 2 。 [1,2,1] 的重要性是 2 + (2) = 4 。
拆分的代价是 2 + 4 = 6 ，可以证明这是所有可行的拆分方案中的最小代价。

示例 3：

输入：nums = [1,2,1,2,1], k = 5
输出：10
解释：将 nums 拆分成一个子数组：[1,2,1,2,1].
[1,2,1,2,1] 的重要性是 5 + (3 + 2) = 10 。
拆分的代价是 10 ，可以证明这是所有可行的拆分方案中的最小代价。

提示：

$1 <= n u m s . l e n g t h <= 1000$
$0 <= n u m s [i] < n u m s . l e n g t h$
$1 <= k <= 10^9$

分析：
我们定义 $f (i)$ 为将前 i 个元素（也就是 0 ~ i - 1下标的元素）拆分的最小代价。所以按照定义，最后的答案为 $f (n)$ 。

状态转移： 对于 $j = [0, i - 1]$ ， $f (i) = min (f [i], f [j] + t r imm e d ([j, j + 1, ... i - 1]) + k)$

时间复杂度： $O(n^2)$

代码：

using LL = long long;
class Solution {
public:
    int minCost(vector<int>& nums, int k) {
        int n = nums.size();

        LL f[n+1];
        //将 f[i] 初始化为无穷大
        for(int i = 0;i <= n;i++) f[i] = 1e10;
        f[0] = 0;
        //cnt 记录区间元素出现的次数
        int cnt[n];

        for(int i = 1;i <= n;i++){
            memset(cnt,0,sizeof cnt);
            //x 记录 [j,i-1] 区间的有效元素个数（即起码出现两次的元素）
            int x = 0;

            for(int j = i - 1;j >= 0;j--){
                ++cnt[nums[j]];
                //只记录出现次数大于2次 的元素
                if(cnt[nums[j]] == 2) x += 2;
                else if(cnt[nums[j]] > 2) x++;

                f[i] = min(f[i],f[j] + x + k);
            }
        }    
        return f[n];
    }
};