一、堆的概念及性质

1.1 什么是堆？

堆是一种完全二叉树（具体在下一章讲述），若二叉树的深度h，除了第h层外其余各层节点数满了，只有第h层缺额且该层结点靠左；任何一个数组可以看作完全二叉树，但不一定是堆。

此外，堆可以分为大根堆和小根堆。根是堆里最大数的完全二叉树称为大根堆，根是堆里最小数的完全二叉树称为小根堆。

大根堆示例

小根堆示例

1.2 堆的性质

堆是一颗完全二叉树；
堆中某结点的值总是不大于或不小于其父节点的值；

二、堆的实现

2.1 算法构思

堆的实现可以使用数组亦可以使用链表，链表的复杂度较高，相比较则数组较低；数组可以利用下标来映射各结点之间的父子或兄弟等关系；此外，数组较链表在尾插上更优。

下面以数组array[ ]={27,15,19,18,28,34,65,49,25,37}为例子，进行算法相关接口思路的构思。

2.1.1 堆的插入

堆的插入接口在构造的时候须注意：

构建堆的数组的存储空间是否满负荷，若满了则须扩容，并在数组未部插入新的数据；
下图为数组插入的示图，此时的二叉树（数组）并不是堆，需要向上调整；

数组构建二叉树

3.若二叉树不是堆，则需要向上调增（默认大根堆，向上调整详见2.1.2节）；

2.1.2 向上调整

通过观察数组存储结构与逻辑关系，可以得出父结点与子结点的相关函数关系：
$childLeft=parent*2+1\\ childRight=parent*2+2\\ parent=(child-1)/2$
上式中，child、parent为数组的下标位置。向上调整具体步骤为：

在构建的堆中，插入整数90，则破坏的堆，此时的插入数90比其父结点大，需要向上调整；
在被影响的子树中，插入的数直接为child，寻找其父结点parent，若子结点比父结点处的值大，则将父子结点处的数值交换；
继续上步操作，比较父子结点的大小，知道child>0结束。

2.1.3 堆的删除

在实际工程应用中，需要删除堆顶，但在本文中为了降低算法复杂度，采用了数组来构造堆，而数组删除首元素需要进行数组迁移。为了降低空间复杂度，我们将数组的首尾元素进行交换，再删除数组的尾部元素，从而间接删除首元素。

此时，需要将新的首元素进行向下调整来维持堆，具体的操作详见下一小节（2.1.4）。

2.1.4 向下调整

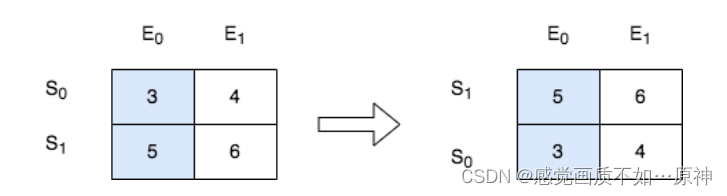
首先将堆中的根90与叶子37进行交换，删除交换到数组尾步的90；接下来通过向下调整来维持大根堆，向下调整具体步骤：

若子结点有两个，则选择子结点中较大的作为child，与parent进行比较；若parent比child小，则进行数值交换，并将parent放置于child的位置；
重新计算child，继续上述步骤；
当child的值等于或超过数组元素的数量时，向下调整结束。

2.2 堆的代码实现

2.2.1 堆的初始化

void HeapInit(HP* php)
{
    assert(php);

    php->a=NULL;
    php->capacity=php->size=0;

}

2.2.2 堆的打印

void HeapPrint(HP* php)
{
    assert(php);
    
    for(int i = 0;i < php->size;i++)
    {
        printf("%d ",php->a[i]);
    }
    printf("\n");
}

2.2.3 堆的销毁

void HeapDestroy(HP* php)
{
    assert(php);

    free(php->a);
    php->a=NULL;
    php->size=php->capacity=0;
}

2.2.4 堆的插入

void HeapPush(HP* php,HPDataType x)
{
    assert(php);

    if(php->size==php->capacity)
    {
        int newCapacity=php->capacity==0?4:php->capacity*2;
        HPDataType* tmp=(HPDataType*)realloc(php->a,sizeof(HPDataType)*newCapacity);
        if(tmp == NULL)
        {
            perror("realloc fail");
            exit(-1);
        }
        php->a=tmp;
        php->capacity=newCapacity;

    }
    php->a[php->size]=x;
    php->size++;
    AdjustUP(php->a,php->size-1);
}

2.2.5 向上调整接口

void AdjustUP(HPDataType* a,int child)
{
    int parent = (child-1)/2;
    while(child>0)
    {
        if(a[child]>a[parent])
        {
            Swap(&a[child],&a[parent]);
            child=parent;
            parent=(child-1)/2;
        }
        else
        {
            break;
        }
    }
}

数值交换函数

void Swap(HPDataType* p1,HPDataType* p2)
{
    HPDataType tmp=*p1;
    *p1=*p2;
    *p2=tmp;
}

2.2.6 堆的元素删除

void HeapPop(HP* php)
{
    assert(php);
    assert(php->size>0);

    Swap(&php->a[0],&php->a[php->size-1]);
    php->size--;
    AdjustDown(php->a,php->size,0);

}

2.2.7 向下调整接口

void AdjustDown(HPDataType* a,int n,int parent)
 {
    int child = parent*2+1;
    while(child<n)
    {
        if((child+1)<n && a[child]<a[child+1])
        {
            ++child;
        }
        if(a[parent]<a[child])
        {
            Swap(&a[parent],&a[child]);
            parent=child;
            child=parent*2+1;
        }
        else
        {
            break;
        }
    }
 }

三、测试

3.1 通过数组array构造堆

void TestHeap()
{
    int array[]={27,15,19,18,28,34,65,49,25,37};
    HP hp;
    HeapInit(&hp);
    for(int i=0;i<sizeof(array)/sizeof(int);i++)
    {
        HeapPush(&hp,array[i]);
    }
    HeapPrint(&hp);
    HeapDestroy(&hp);
}

测试结果：

结果逻辑化，下图所示；本文算法实现了输入数组的建堆功能。

3.2 取堆顶来获取数组的最大数

void TestHeap2()
{
    int array[]={27,15,19,18,28,34,65,49,25,37};
    HP hp;
    HeapInit(&hp);
    for(int i=0;i<sizeof(array)/sizeof(int);i++)
    {
        HeapPush(&hp,array[i]);
    }
    int k=5;
    while(k--)
    {
        printf("%d ",HeapTop(&hp));
        HeapPop(&hp);
    }
    
    HeapDestroy(&hp);
}