作者：@小萌新
专栏：@数据结构进阶
作者简介：大二学生 希望能和大家一起进步！
本篇博客简介：模拟实现高阶数据结构 哈希桶

哈希冲突的另一种解决方法

开散列 – 链地址法

首先对关键码集合使用哈希函数来计算哈希地址 具有相同地址的关键码归于同一子集
每一个子集称为一个桶
每个桶通过一个单链表连接起来 各链表的头节点存放在哈希表中

举例

例如我们使用除留余数法将序列{1, 6, 15, 60, 88, 7, 40, 5, 10}插入到表长为10的哈希表中

当发生哈希冲突的时候我们采取开散列的形式 将哈希地址相同的元素连接到同一个哈希桶下

抽象图大概是这样子

闭散列解决哈希冲突是一种比较野蛮的方式 即我的位置被抢了就去抢别人的位置

而开散列的解决方式就是我们的位置被抢了也没关系 我可以挂在下面

和闭散列不同的是 开散列将相同哈希地址通过单链表连接起来 不会影响与自己不同的哈希地址的增删查改效率 因此开散列的负载因子相比于闭散列而言可以稍微大一点

• 闭散列的负载因子一般在0~0.7之间
• 开散列的负载因子一般在0~1.0之间

因此在实际中 开散列的哈希桶比闭散列的哈希表更加实用

1. 哈希桶的负载因子可以更大 空间利用率更高
2. 哈希桶在极端情况下还有其他的解决方案

下面我们来看一下哈希桶的极端情况

假设我们要插入的元素集合是这样子的{3, 13, 23, 33, 43, 53, 63, 73, 83}

那么我们看看会变成什么样子

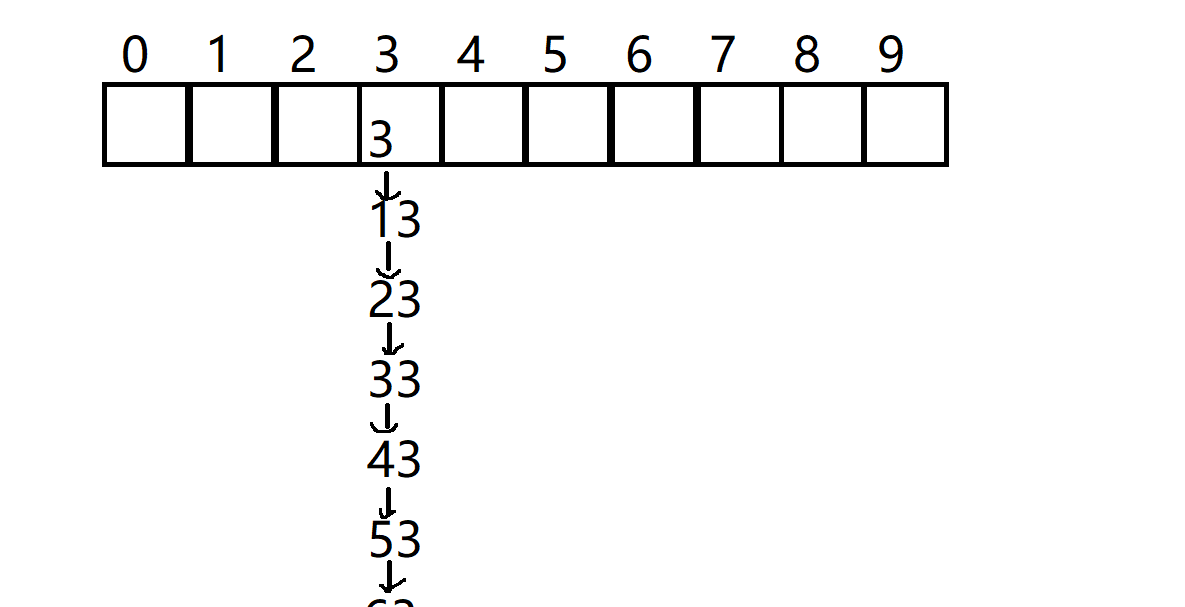
是不是直接退化成单链表了 那么这个时候查找元素的时间复杂度就退化成O(N)了

但是呢 这个时候我们可以将这个单链表转化成红黑树

这样子是不是时间复杂度又被我们优化到Log（N）了 这就是一种底线思维 即考虑最差的情况

为了避免上面说的这种极端情况的出现 一般桶中的节点个数超过8时 我们会将其转化为红黑树

当桶中的节点个数被删除至小于等于八时 我们会将其转化为单链表

哈希表的开散列实现 --哈希桶

哈希表的结构

在开散列的哈希表中 哈希表的每个位置存储的实际上是某个单链表的头结点 即每个哈希桶中存储的数据实际上是一个节点类型 该节点类型除了储存所给数据之外 还要指向下一个节点

节点类的代码如下

template<class K, class V>
struct HashNode
{
	pair<K, V> _kv;
	HashNode<K, V>* _next;

	HashNode(const pair<K, V>& kv) // 列表初始化构造函数
		:_kv(kv),
		_next(nullptr)
	{}
};

和闭散列不同的是 我们不需要为我们哈希表的每一个位置设置一个状态

因为在开散列当中我们将所有经过哈希函数计算后相同的地址放在同一个桶中

我们只需要去桶中寻找 如果桶中没有就是没有了

哈希表的开散列实现形式也需要根据负载因子来判断是否需要扩容 所以我们应该增加一个数据来存储哈希表中的有效元素个数 当负载因子过大时候进行扩容

哈希表的结构大体如下

template<class K, class V>
class HashTable
{
	typedef HashNode<K, V> Node;
public:
private:
	vector<Node*> _table;
	int _n;

};

哈希表的插入

哈希表插入的步骤如下

1. 查看哈希表中是否存在该键值对 若存在则插入失败
2. 判断是否需要调整哈希表的大小
3. 将键值对插入哈希表
4. 调整哈希表的大小

其中哈希表的调整方式如下

• 如果哈希表的大小为0 则扩容至10
• 如果哈希表的负载因子等于1 则先创建一个新哈希表 新的哈希表大小为原来的两倍 之后遍历原哈希表 将其中的所有元素放到新哈希表中 最后将原哈希表和新哈希表交换即可

与上一篇文章中的插入不同的是 我们这里不需要复用插入函数
只需要遍历原节点的时候改变每个节点的位置就可以了

将键值对插入哈希表的方式如下

1. 通过哈希函数计算出对应的哈希地址
2. 若产生哈希冲突 则直接将该结点头插到对应单链表即可

	bool Insert(const pair<K, V>& kv)
	{
		// 1. 查看哈希表中是否存在该键值对
		Node* ret = find(kv.first);
		if (ret)
		{
			return false; // 这里就说明找到了这个节点 如是直接返回false 表示插入失败
		}

		// 2. 判断是否需要调整哈希表的大小
		if (_n == _table.size()) // 哈希表的大小为0 此时负载因子我们定义为1
		{
			vector<Node*> newtable;
			size_t newsize = _table.size() == 0 ? 10 : _table.size() * 2;
			newtable.resize(newsize);


			// 将原哈希表中的所有节点插入到新哈希表中
			for (size_t i = 0; i < _table.size(); i++)
			{
				if (_table[i])// 单链表存在
				{
					Node* cur = _table[i];
					while (cur)
					{
						Node* next = cur->_next;
						size_t index = cur->_kv.first % newtable.size();
						// 将该节点的头插到新哈希表中编号为index的哈希桶中
						cur->_next = newtable[index];//第一次是空 后面就是上面的插入的节点
						newtable[index] = cur;

						cur = next;
					}
					_table[i] = nullptr;
				}
			}
			_table.swap(newtable);
		}

		// 开始插入
		size_t index = kv.first % _table[index];
		Node* newnode = new Node(kv);
		newnode->_next = _table[index];
		_table[index] = newnode;

		_n++;
		return true;
	}

哈希表的查找

哈希表的查找分为以下几步

1. 先判断哈希表中的大小是否为0 为0则查找失败
2. 通过哈希函数计算出一个哈希地址
3. 在这个地址的单链表上寻找 找到则返回 找不到就返回空指针

代码表示如下

Node* Find(const K& key)
	{
		// 首先判断大小是否为0
		if (_table.size()==0)
		{
			return nullptr;
		}
		// 其次经过哈希函数计算找到函数地址
		size_t index = key % _table.size();
		Node* cur = _table[index];

		while (cur)
		{
			if (cur->_kv.first == key)
			{
				return cur;
			}
			cur = cur->_next;
		}
		return nullptr;
	}

哈希表的删除

哈希表的删除实际上就是单链表的删除

大体步骤如下

1. 通过哈希函数计算出对应的哈希桶编号
2. 遍历对应的哈希桶 寻找待删除结点
3. 若找到了待删除结点 则将该结点从单链表中移除并释放
4. 删除结点后 将哈希表中的有效元素个数减一

代码表示如下

	bool Erase(const K& key)
	{
		// 首先找编号
		size_t index = key % _table.size();
		// 之后开始找被删除阶段
		Node* prev = nullptr;
		Node* cur = _table[index];
		while (cur) // cur为空说明遍历完了还没找到直接返回false
		{
			if (cur->_kv.first == key)
			{
				if (prev == nullptr)
				{
					_table[index] = nullptr;
				}
				else
				{
					prev->_next = cur->_next;
				}
				delete cur;
				_n--;
				return true;
			}

			prev = cur;
			cur = cur->_next;
		}
		return false;
	}