⭐博客主页：️CS semi主页
⭐欢迎关注：点赞收藏+留言
⭐系列专栏：C语言进阶
⭐代码仓库：C Advanced
家人们更新不易，你们的点赞和关注对我而言十分重要，友友们麻烦多多点赞＋关注，你们的支持是我创作最大的动力，欢迎友友们私信提问，家人们不要忘记点赞收藏＋关注哦！！！

---

前言

找单身狗这个标题看起来那么地无厘头，可是当大家知道了本题的题目会感觉到原来这是真的单身狗呀！！这么多个数字就这一个数字是单着的，其他数字都是成双成对的，那肯定想法是很多的，我们直接往下看吧！！！

---

一、题目描述

寻找一组数组中只出现过一次的数，分为两种情况：
情况一、仅仅有一个单独出现的数，如下所示：

情况二、有两个单独出现的数，如下所示：

一、先排序再找单身狗再排序

（一）解题思路

是不是很拗口，但是，思路是很简单的，这种寻找方式是能找到多个单身狗，单身狗很多也没关系，我们利用排序的方法，先将这些杂乱的数进行排个序，相同的数肯定是紧紧挨着的，而且本题目是成双成对出现的，仅仅有单身狗，所以不存在有三个同样的数的可能，所以我们可以简单的想象成两个一样的数拉着手坐在一张椅子上，只有落单的那个数单独坐一个椅子，而我们不看双个人只看单个人就是需要跳过两个人，也就是一张板凳即可，这样就有思路了，我们就可以继续往下写代码了。

（二）解题代码

#include<stdio.h>
void bubble_sort(int* arr, int sz) {
	int i = 0;
	for (i = 0; i < sz - 1; i++) {
		int j = 0;
		for (j = 0; j < sz - 1 - i; j++) {
			if (*(arr + j) < *(arr + j + 1)) {
				int temp = *(arr + j);
				*(arr + j) = *(arr + j + 1);
				*(arr + j + 1) = temp;
			}
		}
	}

}
int main() {
	int arr[] = { 1,1,2,2,3,3,4 };
	int pos = 0;
	int sz = sizeof(arr) / sizeof(arr[0]);//算个数
	int arr2[10] = { 0 };//重新封装一个函数用来存放单的值
	bubble_sort(arr, sz);
	int i = 0;
	int j = 0;//arr2数组的计数器
	for (i = 0; i < sz;) {
		if (arr[i] == arr[i + 1]) {//前后两个是一样的就往后跳两个
			i = i + 2;
		}
		else {//前后两个不一样就存放并往后跳一个位置
			arr2[j] = arr[i];
			pos++;
			i++;
			j++;//计数器往后一位
		}
	}
	for (i = 0; i < pos; i++) {//打印
		printf("%d ", arr2[i]);
	}
	return 0;
}

（三）出现的问题

看似我们这个代码很完美了，思路很好，但是也是存在一定的问题的，第一个大问题就是这个代码的时空复杂度都会很高，因为这个代码是先遍历一次整个数组进行排序，再是遍历一次已经排好的数组进行找单身狗，这个数组需要遍历两次，是很麻烦的，万一有个1000个数的数组这么一遍历实在是太慢了；当然，第二个很大的问题是当我们找的那个单身狗在最后一个的话那就会导致越界访问，虽然能够打印出没有任何问题的数据，但是一旦越界访问是十分危险的，因为这个数组越界访问一个数发现那个数并不确定是个什么数，万一是和数组中最后一个单身狗一样的数怎么办，那不是会出现失误吗？？那我们就需要用接下来介绍的方法解决了。

---

二、异或法（仅针对一个单身狗）

（一）解题思路

在之前的学习中我们学过一个操作符叫异或，因为我们知道，异或操作符是两个二进制数相同的为0，相异的为1。同理我们有以下定律：

（二）解题代码

#include<stdio.h>
int main() {
	int dog = 0;
	int arr[] = { 1,2,2,3,3,4,1 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int i = 0;
	for (i = 0; i < sz; i++) {
		dog = dog ^ arr[i];
	}
	printf("这个单身狗是：%d", dog);
	return 0;
}

（三）出现的问题

这个代码看似没问题，但是我们看标题，它是只能针对一个单身狗的，而我们的最终目的是找两个单身狗，那我们仅仅全部再异或一次那完蛋了，出来的数甚至跟里面所有的值都不一样，所以我们该怎么做呢？我们接下来仔细认真看吧！！！

---

三、分组法（针对两个单身狗）

（一）解题思路

我们此时先假设一组数为：1 1 2 2 3 3 4 4 5 6。我们发现，如果有两个单独的数，那我们异或一下发现是5^6，那我们其实就能想到，既然5和6异或出不来两个单身狗，那就分组吧！把这两个单身狗分开分成两组，不能让他俩成了，所以我们就简单分为以下思路：
**第一步：**先全部异或，得到一个异或结果的数。

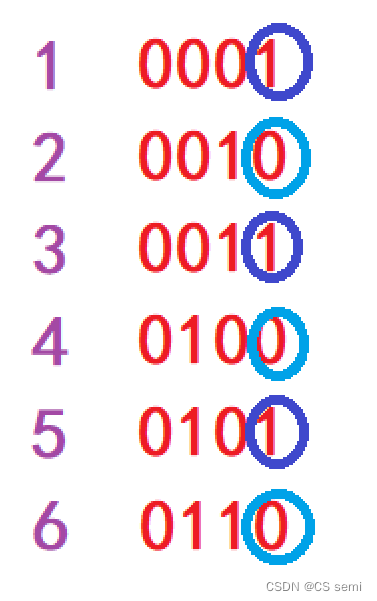
**第二步：**从右往左依次看位，如果与1异或为1，那说明前面的两个单身狗数是在此位是不一样的值，既然值不一样，那就说明可以以这个位进行分割。
**第三步：**我们先把所有的值进行换算成二进制以后，发现是肯定在这个数组中是有情侣数是和单身狗数在某一位是一样的，那有同学问了，这到底什么意思？？？其实啊，很简单，就是单纯把这两个单身狗数分开，其他情侣数是怎么样都没事，因为必然会分到某一组去的，如果都分到同一组了，那也是没关系的，只要最后再来个异或拿出这个单身狗数即可。

（二）解题代码

//代码块1：
#include<stdio.h>
void find_digit(int* arr, int sz) {
	//1.要把所有数字异或
	int i = 0;
	int ret = 0;
	int pos = 0;
	for (i = 0; i < sz; i++) {
		ret ^= *(arr + i);
	}
	//2.计算ret哪一位为1
	for (i = 0; i < 32; i++) {
		if ((ret >> i) & 1 == 1) {//算术右移
			pos = i;
			break;
		}
	}
	//3.把从低位向高的第pos位为1的放在一个组，为0的放在另外一个组
	int num1 = 0;
	int num2 = 0;
	for (i = 0; i < sz; i++) {
		if (((*(arr + i) >> pos) & 1) == 1) {
			num1 ^= arr[i];
		}
		else {
			num2 ^= arr[i];
		}
	}
	printf("%d %d", num1, num2);
}
int main() {
	int arr[] = { 1,2,3,4,5,6,1,2,3,4 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	//进行分组
	//要点：5和6必须在不同的组
	//找出这两个只出现一次的数字
	find_digit(arr, sz);

	return 0;
}

//改进：
#include<stdio.h>
void find_digit(int* arr, int sz, int* px, int* py) {
	//1.要把所有数字异或
	int i = 0;
	int ret = 0;
	int pos = 0;
	for (i = 0; i < sz; i++) {
		ret ^= *(arr + i);
	}
	//2.计算ret哪一位为1
	for (i = 0; i < 32; i++) {
		if ((ret >> i) & 1 == 1) {//算术右移
			pos = i;
			break;
		}
	}
	//把从低位向高的第pos位为1的放在一个组，为0的放在另外一个组
	int num1 = 0;
	int num2 = 0;
	for (i = 0; i < sz; i++) {
		if (((*(arr + i) >> pos) & 1) == 1) {
			num1 ^= arr[i];
		}
		else {
			num2 ^= arr[i];
		}
	}
	*px = num1;
	*py = num2;
}
int main() {
	int arr[] = { 1,2,3,4,5,6,1,2,3,4 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	int x = 0;
	int y = 0;
	//进行分组
	//要点：5和6必须在不同的组
	//找出这两个只出现一次的数字
	find_digit(arr, sz, &x, &y);
	printf("%d %d\n", x, y);

	return 0;
}

（三）展望

这个代码其实已经挺完善的了，但肯定存在不足之处，就是这个单身狗数不确定个数，万一有三个、四个……单身狗数呢！？这个很不确定，但当然肯定有解法的，对于三个我们就是需要先一个再两个，就是做的是第二个解法加上第三个解法，依次类推，但也有一种很难很难的题目，万一这个单身狗数不确定呢！？那我们不知道怎么做了，就需要我们进行先判断有几个再相应思路进行解题，也可以用第一种解法，只不过会比较复杂，如果实在担心数组越界的问题，那就先多加一个值，再将这个值不打印即可。

---

总结

本题的想法和思路有很多，这边总结了两种思路，但当然了，还有更多的解法和更完善的解法等待我们去探索，当我们拥有了这些知识以后，就会知道这些知识的用法和不断巩固！！！

---