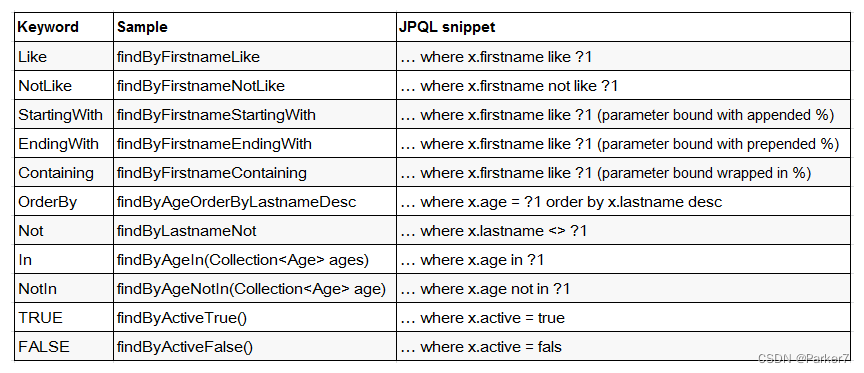
文章目录

一. BF算法
- 1. 算法思想
- 2. 代码实现
二. KMP算法
- 1. 算法思想概述
- 2. 理解基于最长相等前后缀进行匹配
- 3. 代码中如何实现next数组
- 5. 代码实现
- 6. next数组的优化

一. BF算法

1. 算法思想

BF 算法, 即暴力(Brute Force)算法, 是普通的模式匹配算法, 假设现在我们面临这样一个问题: 有一个文本串 S , 和一个模式串 P , 现在要查找 P 在 S 中的位置, 怎么查找呢?

如果用暴力匹配的思路, 并假设现在文本串 S 匹配到 i 位置, 模式串 P 匹配到 j 位置, 则有:

如果当前字符匹配成功 (即 S[i] == P[j] ), 则 i++, j++, 继续匹配下一个字符.
如果失配 (即 S[i] != P[j] ), 令 i = i - (j - 1)，j = 0, 相当于每次匹配失败时, i 回溯至上次开始匹配的下一个位置, j 被置为0; 继续下一次的匹配.

假定我们给出字符串 “ababcabcdabcde” 作为文本串, 然后给出模式串: “abcd” , 现在我们需要查找模式串是否在文本串中出现, 出现返回文本串中的第一个匹配的下标, 失败返回 -1.

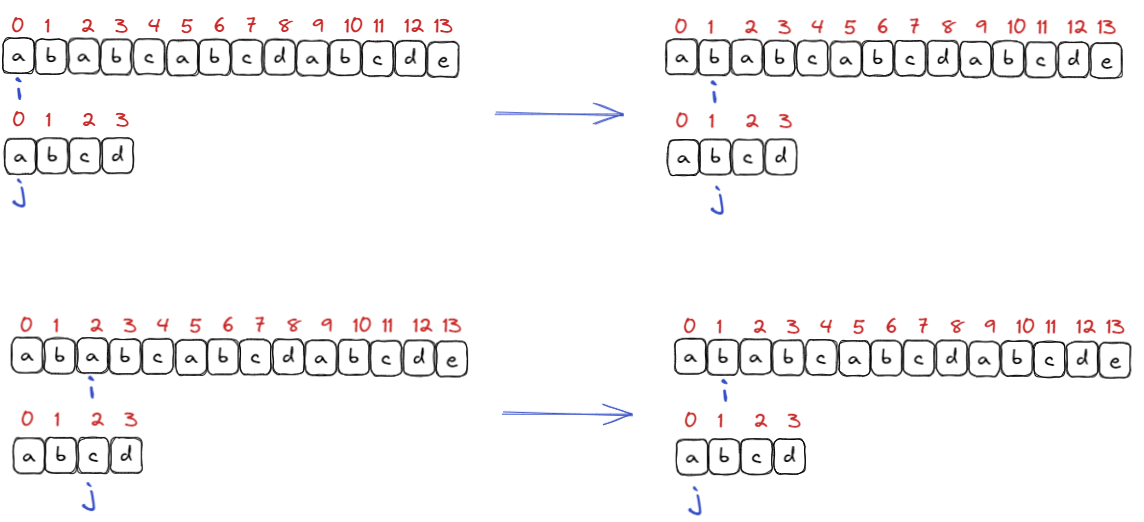只要在匹配的过程当中, 匹配失败, 那么: i 回溯到刚刚开始匹配位置的下一个位, j 回退到0下标重新开始匹配.

可以想到上述回溯的过程其实依靠的是一个循环, 直至匹配成功.

2. 代码实现

理清楚了暴力匹配算法的流程及内在的逻辑, 我们可以写出暴力匹配的代码, 如下:

public class TestBF {
    public static int BF(String str, String sub) {
        //如果给出的字符串为空对象或者空字符串
        if (str == null || sub == null) {
            return -1;
        }
        if (str.length() == 0 || sub.length() == 0) {
            return -1;
        }
        int strLen = str.length();
        int subLen = sub.length();
        int i = 0;
        int j = 0;
        while (i < strLen && j < subLen) {
            if (str.charAt(i) == sub.charAt(j)) {
                // 1. 如果当前字符匹配成功(即S[i] == P[j]),则i++，j++
                i++;
                j++;
            } else {
                // 2. 如果失配(即S[i]! = P[j]),令i = i - (j - 1), j = 0     
                i = i - j + 1;
                j = 0;
            }
        }
        //匹配成功，返回模式串p在文本串s中的位置，否则返回-1  
        if (j >= subLen) {
            return i - j;
        }
        return -1;
    }

    public static void main(String[] args) {
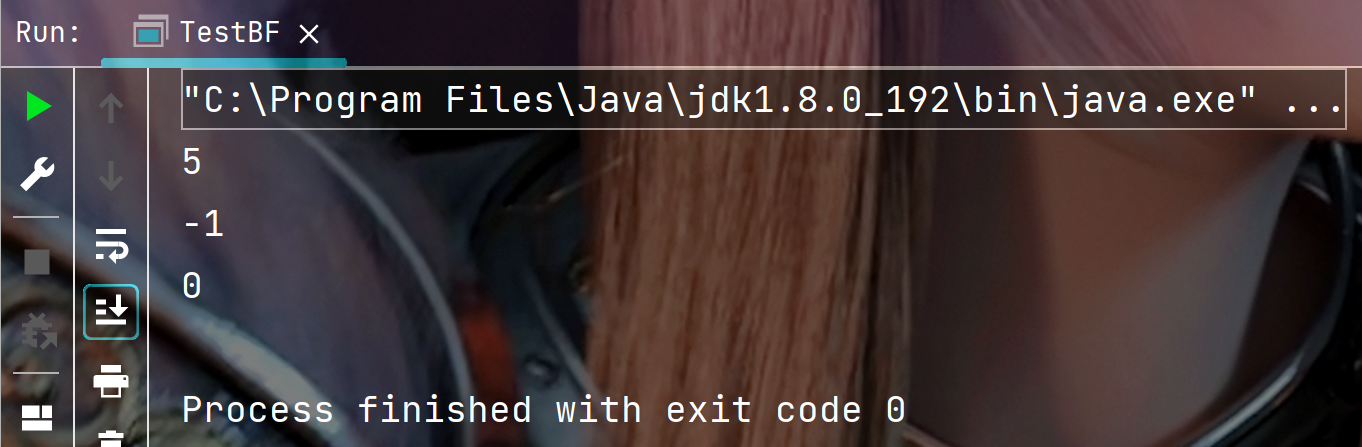
        System.out.println(TestBF.BF("ababcabcdabcde", "abcd"));//5
        System.out.println(TestBF.BF("ababcabcdabcde", "abcdef"));//-1
        System.out.println(TestBF.BF("ababcabcdabcde", "ab"));//0
    }
}

执行结果:

假设 M 是文本串的长度, N 是模式串长度, 则 BF 的时间复杂度最坏为O(M*N).

二. KMP算法

1. 算法思想概述

KMP 算法是一种改进的字符串匹配算法, 由D.E.Knuth, J.H.Morris和V.R.Pratt提出的, 因此人们称它为克努特—莫里斯—普拉特操作 (简称 KMP 算法); KMP 算法相较于上面介绍的暴力求解不一样的是, 这里当两个字符串失配时, 让 i 不往回退, 只需要移动 j 即可, KMP算法就是利用之前已经部分匹配这个有效信息, 保持 i 不回溯, 通过修改 j 的位置, 让模式串尽量地移动到有效的位置.

下面先直接给出 KMP 的算法流程, 然后在后文具体介绍, 假设现在文本串 S 匹配到 i 位置，模式串 P 匹配到 j 位置.

如果 j = -1, 或者当前字符匹配成功(即 S[i] == P[j] ), 都令 i++, j++, 继续匹配下一个字符.
如果 j != -1, 且当前字符匹配失败(即 S[i] != P[j] ), 则令 i 不变，j = next[j], 这个操作意味着失配时, 让 j 回退到的位置其实 “省时” 匹配, 这个操作让 i 在不回退的情况下相当于 i 和 j 已经匹配成功了 next[j] 次, j 就可以到 next[j] 位置和 i 继续匹配了.

这样做就避免了上面暴力匹配中已经匹配过后的重复匹配的过程和一些没必要一些匹配, 看到这里可能还对这个算法迷迷糊糊的, 没关系, 后文会进行解释的.

上面文字中出现的next数组, 下面也会介绍这个数组中各个值的意义, 其实next数组中的值代表的是当前字符之前的字符串中, 最长相等前缀后缀, 例如如果 next [j] = k，代表 j 之前的字符串中有最大长度为*k* 的相同前缀后缀.

这就意味着在某个字符失配时, 该字符对应在的 next 数组中的值会告诉你下一步匹配中, 模式串应该跳到哪个位置 (跳到 next [j] 的位置) , 如果 next [j] 等于 0 或 -1, 则跳到模式串的开头字符，若 next [j] = k 且 k > 0，代表下次匹配跳到 j 之前的某个字符, 而不是跳到开头, 且具体跳过了 k 个字符.

2. 理解基于最长相等前后缀进行匹配

首先什么是前缀和后缀?

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串.
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串

那么最长最长相等前后缀又怎么理解呢?

如果给定的模式串是: “ABCDABD”, 从左至右遍历整个模式串, 其各个子串的前缀后缀分别如下表格所示：

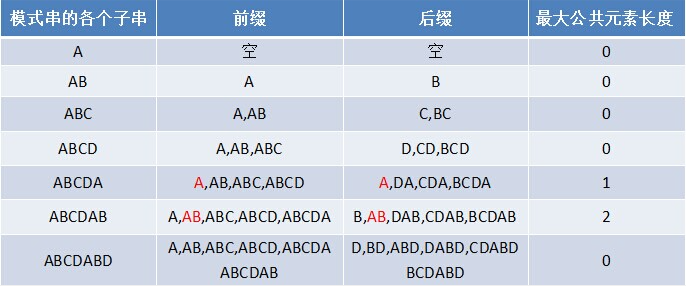
也就是说, 原模式串子串对应的各个前缀后缀的公共元素的最大长度表为:

而在上面介绍中, 当匹配到一个字符失配时, 我们所需要的是当前字符之前的字符串中, 最长相等前缀后缀, 也就是说, 我们每次失配时, 看的是失配字符的上一位字符对应的最大长度值, 而上面的表中是包含当前字符(即失配字符)得到的.

要得到我们所需要的, 只需要上面的表中值整体向右移动一位, 然后初始值赋为-1即可, 这个表中的值即为next数组中的值.

KMP 的精髓就是这个 next 数组了, 也就是用 next[j] = k; 来表示, 不同的 j 来对应一个 k 值，这个 k 就是你将来要移动的 j 要移动的位置.

通过上面的介绍, k 值求法符合这样的规则:

认为当前字符是和文本串配配失败的, 找到不包含当前字符, 以下标为 0 的字符开始, 以 j-1 下标的字符结尾, 匹配成功部分的两个最长相等的真子串(即最长相等前缀后缀), k的值即为这个最长真子串的长度.
不管什么数据 next[0] = -1; next[1] = 0;

下面来理解为什么要基于这个 next 表中的值来进行匹配:

假定我们给出字符串 “cdabcababcabca” 作为文本串, 然后给出模式串: "abcabc" , 现在我们需要查找模式串是否在文本串中出现, 出现返回文本串中的第一个匹配的下标, 失败返回 -1;

在文本串和模式串进行遍历, 匹配到如下位置的时候, 进行观察:

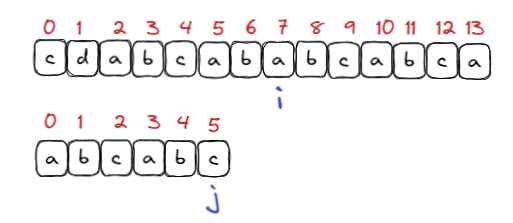
此时文本串和模式串分别在 7 下标和 5 下标匹配失败, 按照暴力匹配的逻辑, 此时 i 应该回溯到文本串的 3 下标, j应该回到模式串的 0 位置重新开始匹配, 但这个匹配是没有必要的, 因为文本串的 3 下标和模式串的 0 位置字符也是没有必要的, 而KMP就可以减少这些不必要的匹配过程.

KMP可以复用已经匹配过的那一部分字符串,

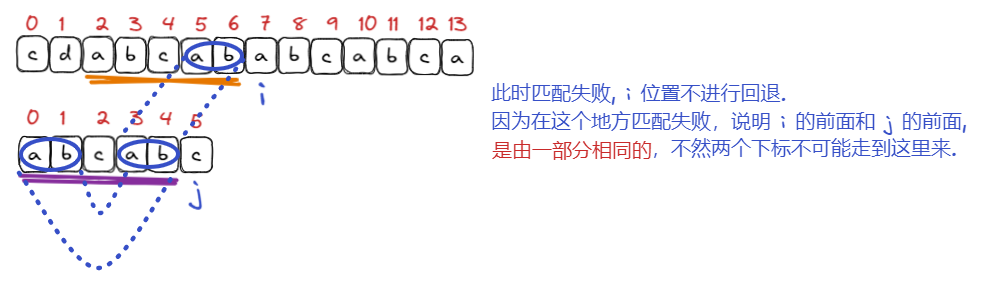
而我们利用的就是这部分相同的信息, 此时需要找出在模式串 当前字符前面的字符串中的最长相等前缀后缀, 很明显, 上面的最长相等前后缀是ab, 也就是说此时 next 数组中 j 位置放置的值就是 2 , 在两个字符串这部分相同的字符中, 有文本串中 5, 6 位置的字符和模式串中 3, 4 位置的字符相同, 而模式串中存在最长相等前缀后缀, 即0, 1位置的字符和 3, 4位置的字符是相同的, 所以这种情况下文本串中 5, 6 位置的字符和模式串中 0, 1 位置的字符一定是相同的.

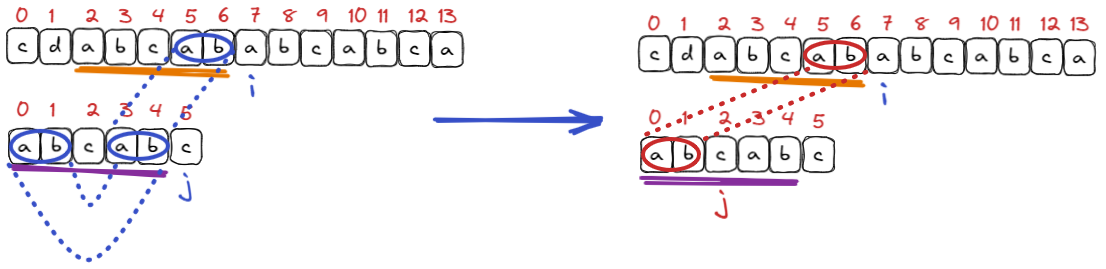
此时就可以让 i 位置不变, j 回退到 2 位置(也就是最长相等前后缀的长度)继续进行匹配, 这就相当于文本串和模式串已经匹配成功了两次, 开始进行第三次匹配.

这个过程就是KMP的精髓所在了, 这样的操作就是通过 next 数组进行预处理出来的结果, 避免了重复匹配的过程, 而且这样 i 不回退也避免了很多没必要的比匹配, 比如从文本串3, 4位置开始的和模式串的匹配.

上面的一大堆, 主要是介绍了什么是前缀后缀, 以及如何求字符串中的最长相等前后缀, 我们可以手动得到 next 数组, 最重要的是理解 next 数组中值的由来和作用, 相信通过上面的内容伙伴们可以对这里有一定的理解.

3. 代码中如何实现next数组

如下图所示, 假定给定模式串 “abcababcaba” , 且已知 next [j] = k (相当于 “p0 pk-1” = “pj-k pj-1” = abca, 可以看出 k 为 4), 现要求得 next [j + 1] 等于多少?

因为 pk = pj = b, 所以 next[j + 1] = next[j] + 1 = k + 1 (可以看出 next[j + 1] = 5), 代表字符 c 前的模式串中，有长度 k+1 的最长相等前后缀.

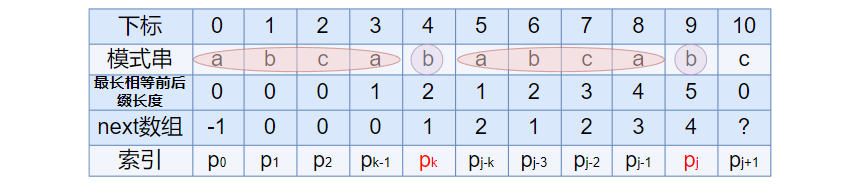
但如果 pk != pj 呢? 此时说明 “p0 pk-1 pk” ≠ “pj-k pj-1 pj”, 也就是说, 当 pk != pj 后, 字符 c 前有多大长度最长相等前后缀呢？

很明显, 因为 b 不同于 a, 所以 abcab 跟 abcaa 不相同, 即字符 c 前的模式串没有长度为k+1的最长相等前后缀; 也就不能再简单的使 next[j + 1] = next[j] + 1 了; 所以, 咱们只能去寻找长度更短一点的相等前后缀.

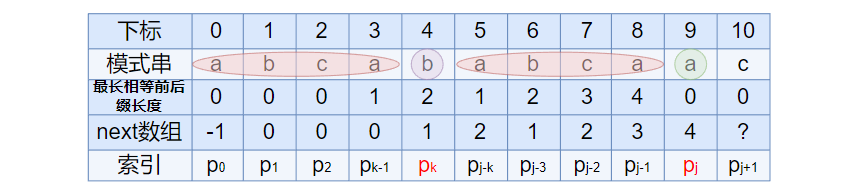
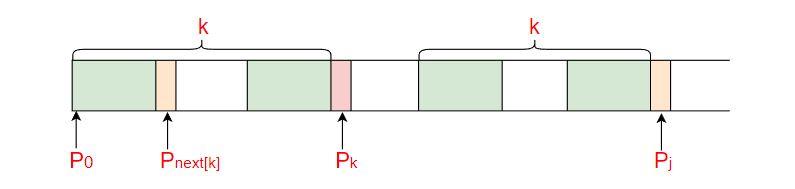
结合上图来讲, 若能在前缀 “p0 pk-1 pk” 中不断的递归前缀索引 k = next [k], 找到一个字符 pk’ 也为 a，代表 pk’ 位置的字符 = pj 位置处的字符, 且满足 p0 pk’-1 pk’ = pj-k’ pj-1 pj, 则最大相同的前缀后缀长度为 k’ + 1, 从而 next [j + 1] = k’ + 1 = next [k’ ] + 1; 如果递归过程中没有一个位置等于a, 则代表没有相同的前缀后缀，从而 next [j + 1] = 0;

就像上面的情况下, 下一次 k 就等于 1, 1 下标处字符还是 b 和 a 不相同, 那么再 k 的值就为 0, 0 下标处的字符是 a 和 a 相同(即 pk’ = pj = a ), 此时 next[j + 1] = k’ + 1 = 1, 代表字符 c 前的模式串中，有长度为 1 的最长相等前后缀.

那为何递归前缀索引 k = next[k], 就能找到长度更短的相同前缀后缀呢?

这里其实还是需要对 next 数组的有一定的理解, next 数组中的值代表是最长相等前后缀, 也就是是字符串中有两个相等的真子串, 所以我们就再去这部分前缀子串中继续寻找长度更短的相等前后缀, 不断的递归 k = next[k] , 直到要么找到长度更短的相等前后缀, 要么没有长度更短的相等前后缀, 看下图进行理解, 这里看图更直观容易理解一些.

所以基于上述理解, 写出下面的代码来求 next 数组:

private static void getNext(int[] next, String sub) {
    next[0] = -1;//数组中的第一个值为-1
    //如果模式串的只有一个字符,则数组就没有后面的值了
    if (sub.length() == 1) {
        return;
    }
    next[1] = 0;//数组的第二个值为0
    int k = 0;//根据前一项k,求下一项i位置的k.
    int i = 2;//即已知了i-1位置的k,求i位置的k.

    while (i < sub.length()) {//next数组还没有遍历完
        //sub.charAt(k)表示前缀,sub.charAt(i-1)表示后缀,判断是否相等
        if ((k == -1) || (sub.charAt(k) == sub.charAt(i-1))) {
            next[i] = k+1;
            k++;
            i++;
        } else {
            k = next[k];
        }
    }
}

5. 代码实现

有了上面了理解, KMP 的算法流程就差不多能理清理解了了, 这里再总结一下:

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置:

如果 j = -1, 或者当前字符匹配成功(即 S[i] == P[j] ), 都令 i++, j++, 继续匹配下一个字符.
如果 j != -1, 且当前字符匹配失败(即 S[i] != P[j] ), 则令 i 不变, j = next[j], 这个操作意味着失配时, 让 j 回退到的位置其实 “省时” 匹配, 这个操作让 i 在不回退的情况下相当于 i 和 j 已经匹配成功了 next[j] 次, j 就可以到 next[j] 位置和 i 继续匹配了.

KMP 避免了像暴力匹配中已经匹配过后的重复匹配的过程和一些没必要一些匹配.

所以最终的代码效果如下:

public class TestKMP {
    public static int KMP(String str, String sub) {
        //传入的字符串是空对象
        if (str == null || sub == null) {
            return -1;
        }
        int strLen = str.length();
        int subLen = sub.length();
        //传入的字符串长度为0
        if (strLen == 0 || subLen == 0) {
            return -1;
        }
        int i = 0;//遍历文本串
        int j = 0;//遍历模式串

        //定义next数组,和模式串的长度相同
        int[] next = new int[sub.length()];
        //对next数组进行赋值处理
        getNext(next, sub);

        while (i < strLen && j < subLen) {
            //注意j=-1的处理
            if((j == -1) || (str.charAt(i) == sub.charAt(j))) {
                //匹配成功
                i++;
                j++;
            } else {
                //匹配失败
                j = next[j];
            }
        }

        if (j >= subLen) {
            return i - j;
        }
        return -1;
    }

    private static void getNext(int[] next, String sub) {
        next[0] = -1;//数组中的第一个值为-1
        //如果模式串的只有一个字符,则数组就没有后面的值了
        if (sub.length() == 1) {
            return;
        }
        next[1] = 0;//数组的第二个值为0
        int k = 0;//根据前一项k,求下一项i位置的k.
        int i = 2;//即已知了i-1位置的k,求i位置的k.

        while (i < sub.length()) {//next数组还没有遍历完
            //sub.charAt(k)表示前缀,sub.charAt(i-1)表示后缀,判断是否相等
            if ((k == -1) || (sub.charAt(k) == sub.charAt(i-1))) {
                next[i] = k+1;
                k++;
                i++;
            } else {
                k = next[k];
            }
        }
    }

    public static void main(String[] args) {
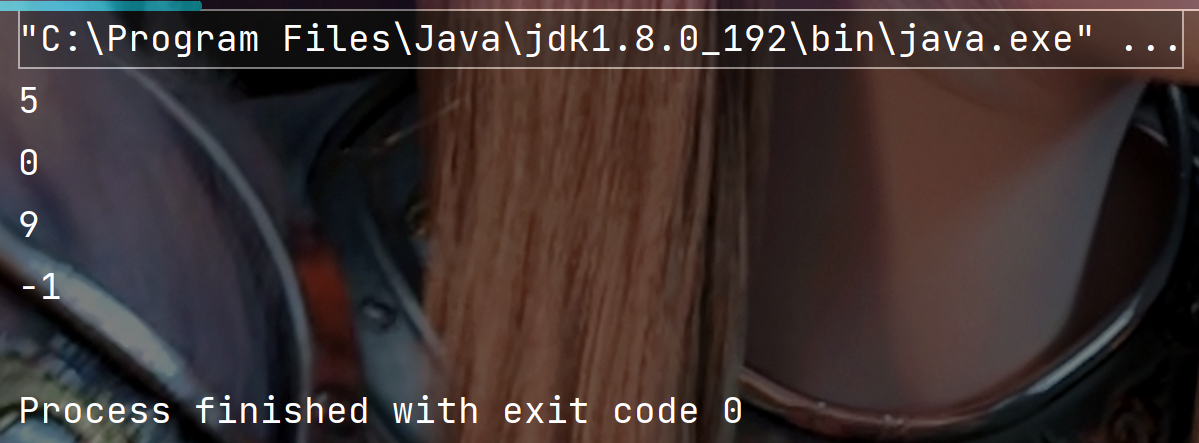
        System.out.println(KMP("ababcabcdabcde","abcd"));//5
        System.out.println(KMP("ababcabcdabcde","ab"));//0
        System.out.println(KMP("ababcabcdabcde","abcde"));//9
        System.out.println(KMP("ababcabcdabcde","abcdef"));//-1
    }
}

执行结果:

6. next数组的优化

到这里, 上面的内容已经介绍了 BF 暴力匹配的原理和代码, KMP 算法的原理, 流程和流程之间的内在逻辑联系, 以及 next 数组的手动推导和代码求解, 其实这里的代码还可以优化.

考虑下面的场景, 有以模式串为: “aaaaaaaab”, 则这个串的next数组就是: -1,0,1,2,3,4,5,6,7 , 那么这里为什么要进行优化, 假设在匹配过程中是在模式串的七下标处匹配失败了, 那么就要递归 k 的值去寻找再比之短的相等前后缀(即递归 k = next[k] ), 当如果是这里的字符串, k 回退一步得到的字符还是 a, 再接着退还是 a, 那么有没有办法让这里的回退一步到位呢(这里就是说一次回退直接回退到 -1 ).

那么这里优化后的数组就叫做 nextVal 数组, 首先得到 next 数组, 然后遍历这里的 next 数组,

如果当前位置的字符和当前位置失配后要回退到的位置字符不相等, 就还写自己位置的 next 数组中的值, 如果不相等, 就写回退位置的那个 nextVal 数组中的值.

所以上面的的字符串, nextVal 数组中的值如下:

再比如:

所以可以针对 next 数组的方法可以加上如下的优化代码:

private static void getNext(int[] next, String sub) {
    next[0] = -1;//数组中的第一个值为-1
    //如果模式串的只有一个字符,则数组就没有后面的值了
    if (sub.length() == 1) {
        return;
    }
    next[1] = 0;//数组的第二个值为0
    int k = 0;//根据前一项k,求下一项i位置的k.
    int i = 2;//即已知了i-1位置的k,求i位置的k.

    while (i < sub.length()) {//next数组还没有遍历完
        //sub.charAt(k)表示前缀,sub.charAt(i-1)表示后缀,判断是否相等
        if ((k == -1) || (sub.charAt(k) == sub.charAt(i-1))) {
            next[i] = k+1;
            k++;
            i++;
        } else {
            k = next[k];
        }
    }

    //优化操作,数组中0下标值为-1(会越界),所以从1下标开始遍历
    for (int j = 1; j < next.length; j++) {
        //当前位置和要回退的位置的字符进行
        if (sub.charAt(j) == sub.charAt(next[j])) {
            //当前位置和要回退的位置的字符相等,将next数组中的值更新
            next[j] = next[next[j]];
        }
        //不相等就保持原来的值
    }
}