一起自学SLAM算法：7.5 基于因子图的状态估计

news2025/1/20 2:52:39

连载文章，长期更新，欢迎关注：

虽然式（7-90）所示的完全SLAM系统可以用滤波方法求解，比如著名的Fast-SLAM实现框架。但是，贝叶斯网络表示下的完全SLAM系统能很方面地转换成因子图表示，这部分内容已经在7.2.4节中讨论过了。利用因子图表示完全SLAM问题，然后用最小二乘估计进行求解会更方便。这样贝叶斯网络中的最大后验估计就等效为因子图中的最小二乘估计，这种最小二乘估计常常是非线性最小二乘估计。

求解该非线性最小二乘问题的方法大致上有两种，一种方法是先对该非线性问题进行线性化近似处理，然后直接求解线性方程来得到待估计量；另一种方法并不直接求解，而是通过迭代策略，让目标函数快速下降到最值处，对应的估计量也就求出来了。常见的迭代策略有steepest descent、Gauss-Newton、Levenberg-Marquardt、Dogleg等，这些迭代策略被广泛应用在机器学习、数学、工程等领域，有大量的现成代码实现库，比如Ceres-Solver、g2o、GTSAM、iSAM等。

本节内容旨在通过对非线性最小二乘问题解法的分析，让大家理解优化方法的基础原理。经过线性化近似后直接求解非线性最小二乘，这种直接求解方法的典型实现框架Graph-SLAM将在7.7.3节中详细讨论；另一种方法是采用迭代方式间接求解，也就是所谓的优化方法，在7.7.4节所介绍的现今主流SLAM算法中大多数都基于这种优化方法。

7.5.1 非线性最小二乘估计

式（7-50）已经给出了描述SLAM问题的最小二乘形式，式中包含2种类型的约束，即运动约束和观测约束。为了更一般地进行最小二乘的讨论，这里将这2种类型的约束用统一的方式来表述，那么式（7-50）就可以改写成式（7-123）所示的形式。由于式中的函数 $f$ 通常是非线性函数，所以这是一个非线性最小二乘。

7.5.2 直接求解方法

要求解式（7-123），可以将函数 $f$ 进行线性化近似，这样就能将非线性最小二乘转化成线性最小二乘，然后直求解线性方程就能得到线性最小二乘的解。可以采用泰勒展开进行线性化，泰勒展开公式如下式（7-124）所示。也就是说非线性函数 $f(x)$ 在 $x_{0}$ 附近的局部区域取值可以用泰勒级数来近似。

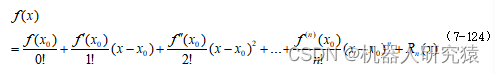
在没有特别精度要求时，可以用最简单的一阶泰勒展开对式（7-123）中的非线性函数 $f(x_{i})$ 进行线性化，如式（7-125）所示。其实这一线性化过程已经在7.4.2节中的扩展卡尔曼滤波中讲解过了，展开点 $x0_{i}$ 一般取状态量 $x_{i}$ 的均值， $F_{i}$ 是函数 $f(x_{i})$ 在 $x_{i}=x0_{i}$ 处的一阶导数。

那么，将式（7-125）代入式（7-123），就将非线性最小二乘转化成线性最小二乘了，如式（7-126）所示[7] p20~21。其中协方差矩阵 $\Sigma _{i}^{-1}$ 可以开平方后放到平方运算里面去，并将平方运算里面的式子进行整理，与变量 $x_{i}$ 无关的常数项用 $b_{i}$ 表示，变量 $x_{i}$ 的系数用 $A_{i}$ 表示。

在理想情况下， $\sum_{i}^{}\left \| b_{i}-A_{i}\cdot x_{i} \right \|^{2}$ 可以取到最小值0。而 $\sum_{i}^{}\left \| b_{i}-A_{i}\cdot x_{i} \right \|^{2}$ 取0值，可以等价于求和累加的每一项 $b_{i}-A_{i}\cdot x_{i}$ 都取0值，数学表达如式（7-127）所示。

通过式（7-127）可以看出，线性最小二乘的直接求解方法，就是解 $Ax=b$ 这个线性方程。大家可能最容易想到，直接对 $A$ 求逆，就能解出 $x=A^{-1}b$ 。实际情况， $A$ 往往为不可逆矩阵，所以不能直接求逆运算。该线性方程通常采用数值方法解算，比如Cholesky分解和QR分解。

首先来看一下Cholesky分解求 $Ax=b$ 线性方程的过程，如式（7-128）所示。先在方程两边左乘 $A^{T}$ ，然后利用Cholesky分解将 $A^TA$ 分解成 $n\times n$ 的上三角矩阵 $R$ 的乘积 $R^TR$ 。令新的变量 $y=Rx$ ，那么就得到新的 $R^Ty=A^Tb$ 线性方程，由于 $R$ 是上三角方阵，其转置 $R^T$ 则为下三角方阵，那么很容易从上到下依次解 $R^Ty=A^Tb$ 中的线性方程而求出 $y$ 。求出 $y$ 之后，利用 $R$ 是上三角方阵的性质，也很容易从下到上依次解 $Rx=y$ 的线性方程而求出 $x$ ，这样原来的 $Ax=b$ 线性方程就求解出来了。

另一种比Cholesky分解数值更精确和稳定的方法是QR分解，如式（7-129）所示。利用QR分解将 $A$ 分解成矩阵 $Q$ 和矩阵 $R$ 的乘积，其中 $Q$ 是正交矩阵（即 $Q^{-1}=Q^{T}$ ）， $R$ 是上三角矩阵。接着，在方程两边左乘 $Q^{-1}$ 对方程化简，并利用 $Q^{-1}=Q^{T}$ 就可以得到新的 $Rx=Q^{T}b$ 线性方程。跟Cholesky分解中的方法一样，由于 $R$ 是上三角矩阵，那么很容易从下到上解 $Rx=Q^{T}b$ 线性方程而求出 $x$ ，这样原来的 $Ax=b$ 线性方程就求解出来了。

7.5.3 优化方法

由于实际SLAM问题的非线性最小二乘中，很难找到合适的线性化方法，初值也比较难确定，并且代价函数的误差往往不能最小化到0值，所以上面介绍的直接求解方法很难利用在实际问题中。下面就来介绍求解非线性最小二乘最常用的方法，即优化方法。优化方法并不直接求解代价函数来得出解析形式的解，而是通过迭代的方法，按照一定的策略不断调整自变量的取值使代价函数逐渐变小，当代价函数不再下降或者下降幅度很小时迭代就完成了。接下来介绍5种流行的迭代策略，即梯度下降算法、最速下降算法、高斯-牛顿算法、列文伯格-马夸尔特算法和狗腿算法。

1.梯度下降算法