插入排序
从第二个数,往前面进行插入,默认第一个数字有序,插入第二个,则前两个都有序了,一个一个往后选择数字,不断向前进行插入
直接插入排序
时间复杂度:
最好情况:全部有序,此时只需遍历一次,最好的时间复杂度为O ( n )
最坏情况:全部反序,内层每次遍历已排序部分,最坏时间复杂度为 O(N^2)
综上,因此直接插入排序的平均时间复杂度为O(N^2)
空间复杂度:
没有使用多余的空间,是在原数组上进行操作,所以时间复杂度为O(1)
稳定性:
稳定的,相同大小的数字前后位置不变
思路举例:

代码详细实现:
public void sort(int[] arr) {
if (arr == null || arr.length == 0) return;
//由于起始的时候,第一个数已经排好,从后面开始插入即可,所以这个循环从1开始即可
for (int i = 1; i < arr.length; i++) {
int temp = arr[i];//暂时存放需要插入的数
int j;
//由于需要与前面排好序的进行比较 且 从后往前比较,所以j从i-1开始到0结束
for (j = i - 1; j >= 0; j--) {
if (arr[j] > temp) {
//如果前面的数大于temp 则这个前面的数向后移动一下
arr[j + 1] = arr[j];
} else {
//出现<=temp的数字直接跳出循环
break;
}
}
//跳出循环之后,把temp放入j+1的位置,temp就插入好了
arr[j + 1] = temp;
}
}希尔排序
希尔排序其实是直接插入排序的升级版本,不过是把 数组进行分组然后进行插入排序
时间复杂度:大约在O(n ^ 1.25)到O(1.6 * n ^ 1.25)取决于增量gap的值
稳定性:不稳定
空间复杂度:O(1)
适用场景:相比直接插入排序,希尔排序更适合无序的数据,尤其数据量大的时候,能节省很多运行时间
思路举例:选取增量,进行分组排序,其实相比于直接插入排序就是多了一个分组增量,在代码中体现就是多套一个while循环来改变增量的值

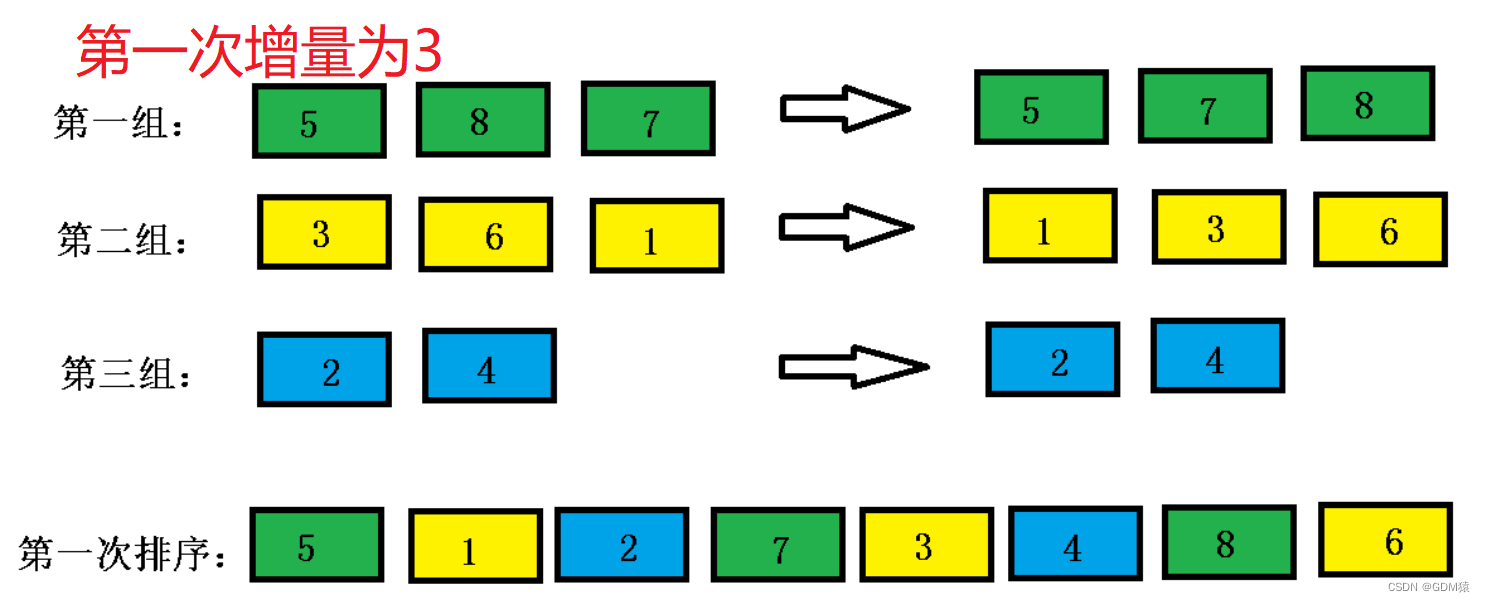

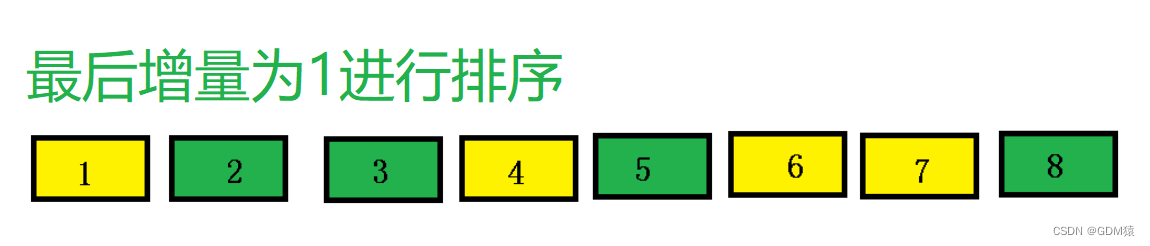
代码实现:
public void sort(int[] arr) {
//这里图简单 我们直接使用gap每次/2来确定gap的值
int gap = arr.length;
while (gap != 1) {
gap /= 2;
//下面的步骤其实和 直接插入排序一样 不过是每次增加gap
for (int i = 1; i < arr.length; i += gap) {
int j;
int temp = arr[i];
for (j = i - 1; j >= 0; j--) {
if (arr[j] > temp) {
arr[j + 1] = arr[j - 1];
} else {
return;
}
}
arr[j + 1] = temp;
}
}
}选择排序
每次从待定元素中,选出最小的那个,然后放在序列的起始位置,继续排序后面的。
直接选择是每个找一遍选择,堆排序是利用大根堆,找最大的放到后面
直接选择排序
时间复杂度:O(N^2)(对数据是否有序不敏感)
空间复杂度:O(1)
稳定性:不稳定过程 每次选出一个最小值放到数据的第一个位置
过程:不断选出最小的,分别放到第一个位置,第二个位置
代码:
//普通版本:找到最小的放到左边
publicvoidselectSort(int[] array) {
for (inti=0; i < array.length; i++) {
intminIndex= i;
for (intj= i + 1; j < array.length; j++) {
if (array[j] < array[minIndex])
{ minIndex = j;}
}
swap(array, minIndex, i);
}
}
//升级优化版本:左右两边同时进行,同时找出最大和最小的
publicvoidselectSortPro(int[] array) {
int left, right;
for (left = 0, right = array.length - 1; left < right; left++, right--) {
intminIndex= left;
intmaxIndex= right;
for (intj= left ; j <= right; j++) {
if (array[j] < array[minIndex]) { minIndex = j;}
elseif (array[j] > array[maxIndex]) { maxIndex = j;}
}
swap(array, left, minIndex);
//如果left位置存放的是最大值,则下一步maxIndex的内容被掉包了,要有个if判断一下if (left == maxIndex) { maxIndex = minIndex; }
swap(array, right, maxIndex);
}
}堆排序
是直接选择排序的优化,相较于直接选择排序, 通过堆的方式 选择 最小值放在前面
时间复杂度:O(N*logN)(大/小根堆调整一次的时间复杂度是 logN)
空间复杂度: O (1)
稳定性: 不稳定
思路过程:加入堆的数据结构,升序使用大根堆,降序使用小根堆
代码:
public void heapSort(int[] arr) {
createdHeap(arr);//把原来的函数变成大根堆
for (int i= arr.length - 1; i > 0; i--) {
swap(arr, 0, i);//大根堆 arr[0]最大 把他挪到最后面
shiftDown(arr, 0, i);//再继续对 arr
}
}
//建立大根树的方法
private void createdHeap(int[] arr) {
int len= arr.length;
for (int i= len - 1; i >= 0; i--) { shiftDown(arr, i, len); }
}
//向下寻找 ---- 注意这个代码一定要立马能写出来
private void shiftDown(int[] arr, int parent, int len) {//能够操作的界限是 parent 到 len-1
int son= parent * 2 + 1;//左孩子的位置
while (son < len) {
if (son+1 < len && arr[son] < arr[son+1]){ son++; }//找到左右孩子比较大的那一个大孩子
else {
if (arr[parent] < arr[son]) {//如果大孩子 比 父亲大 那么就交换
swap(arr, parent, son);
parent = son;
son = parent * 2 + 1;
} else { break; }
}
}
}
交换排序
选出一个较大的数和一个较小的数,交换位置。将小数放前面,大数放到后面。
冒泡排序
是一个很简单的排序,编写最简单代码且不要求什么的时候可以使用。
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
思路:每次交换把大的数都换到后面。每个循环能把最大的数,交换到最后面的位置。
代码:
public void bubbleSort(int[] arr) {
//记住两个for的结束条件
for (int i=0; i < arr.length - 1; i++) {
for (int j=0; j < arr.length - 1 - i; j++) {
if (arr[j]>arr[j+1]){ swap(arr,j,j+1); }
}
}
}`快速排序
时间复杂度:O(N*logN)
空间复杂度:O(log2n)~O(n) ( 有序数据 的空间复杂度是O(N))
稳定性:不稳定
适用场景:相较于希尔排序,更适合无序,因为是递归有序的情况可能造成堆满
方法:递归,基本写法和树类似
先写一个sort函数,脱裤子放屁,让使用者只传入一个数组即可
写quicklySort函数,参数有 arr,left,right,负责递归,只要right还小于left就不断进行递归执行。
写核心代码 参数依旧是arr,left,right,但返回值为root,负责排序实现。具体的实现方法有下面三种,Hoare版本,挖坑法(个人认为最简答的),双指针法。
代码:
Hoare版
任意选取待排序序列中的一个元素作为基准值,按照该排序码将待排序集合分割成两个子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后再对左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
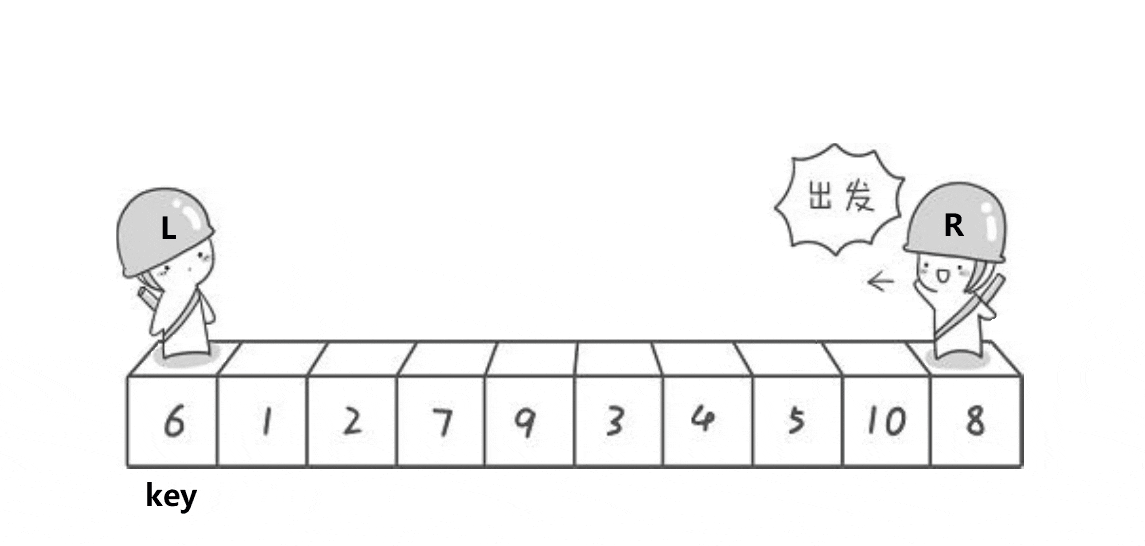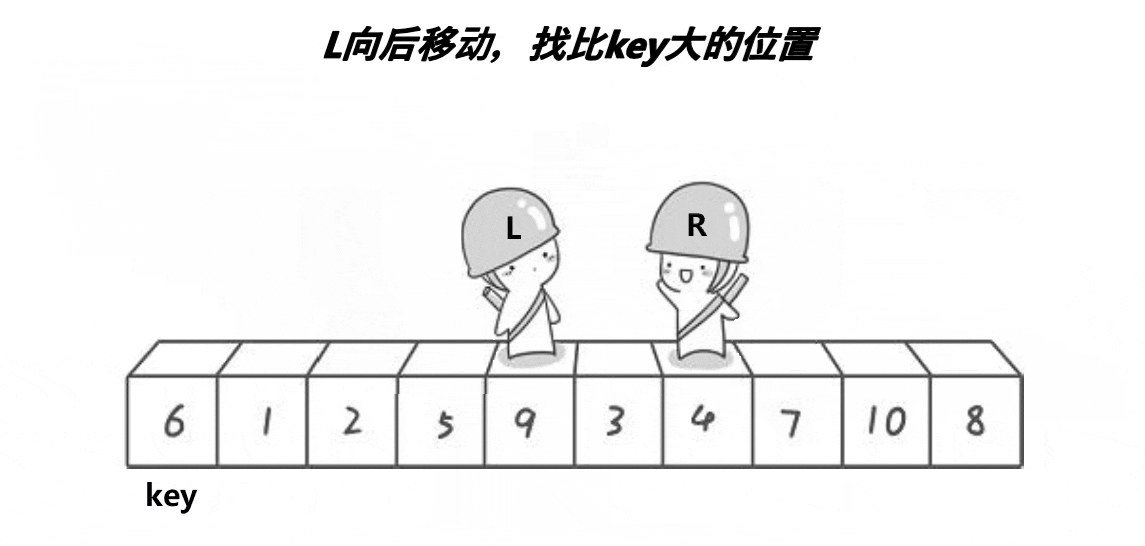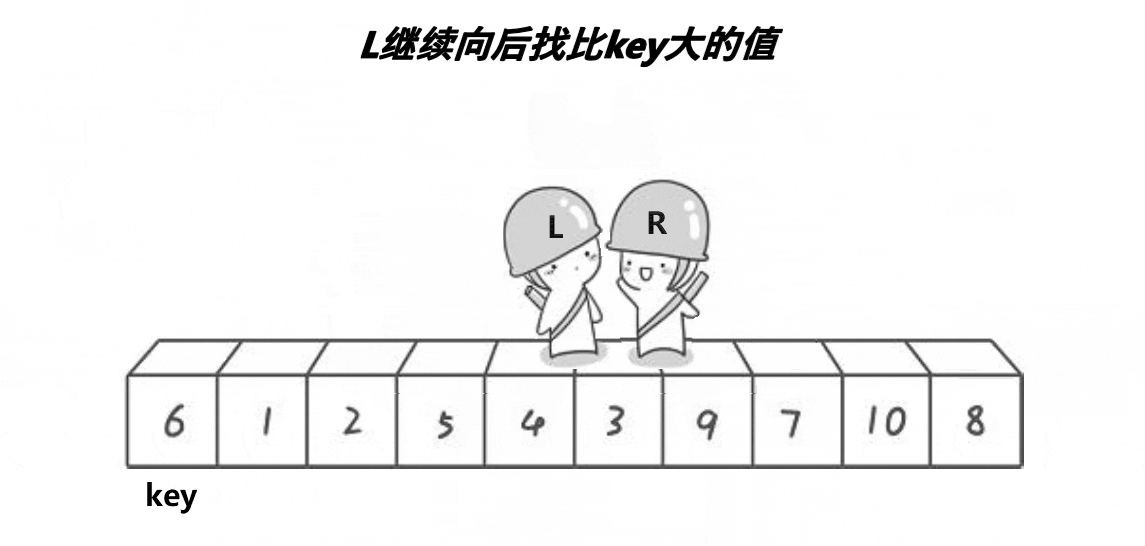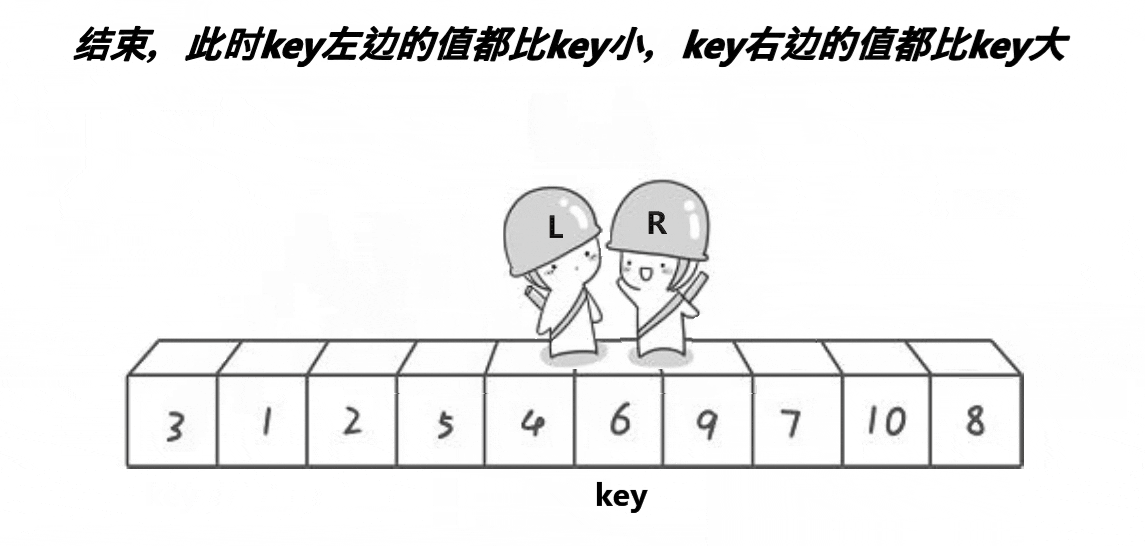
//脱裤子放屁,让使用者只需要传入一个数组就可以排序
public void quicklySort(int[] arr) {
quicklySort(arr, 0, arr.length - 1);//传入数组和数组的左右边界
}
private void quicklySort(int[] arr, int left, int right) {
if (left >= right) return;
int root = hoare(arr, left, right);
quicklySort(arr, root + 1, right);//操作左子序列
quicklySort(arr, left, root - 1);
}
private int hoare(int[] arr, int left, int right) {
int root = left;
while (right > left) {
//为啥要取等号?不取就死循环了,一直交换
while (right > left && arr[right] >= arr[root]) {
right--;
}
while (right > left && arr[left] <= arr[root]) {
left++;
}
swap(arr, left, right);//这里使用交换,跟挖坑法有所区别
}
swap(arr, root, left);
return left;
}挖坑法
挖坑法大体思路与hoare法思路相同
基本思想是:将基准值保存到标记位中,这样最右侧位置就形成了一个坑位,然后左侧标注位往右遍历找比基准值大的元素,找到后将该元素填入右侧坑位中,该位置就又形成了一个新的坑位,坑位不断左右变换,重复上述过程直到左右标志位相遇,最后将基准值放入最后的坑位中,最对左右子序列重复上述过程直到整个序列排序完成。
public void digQuicklySort(int[] arr){
digQuicklySort(arr,0,arr.length-1);
}
private int digQuicklySort(int[] arr,int left,int right){
int root = dig(arr,left,right);
digQuickluSort(arr,root+1,right);
digQuickluSort(arr,left,root+1);
return root;
}
private int dig(int[] arr,int left,int right){
int root= arr[left];//key存放基
while(left<right){//注意比较挖坑法与Hoare的区别
while(left<right && arr[right]>=root){ right--; }
arr[left] = arr[right];//这时候右边较大值,放到了左边,而坑到了右边
while(left<right && arr[left]<= root){ left++; }
arr[right] = arr[left];//这时候左边较小值又把右边的坑填了,而左边有了坑
}
arr[left] = root;//把root基 补到中间的坑
return left;
}面试:手写快排.....如何能优化一下?.....
快速排序优化
优化1.中位数做基
问题:快速排序不适合基本有序数据
原因:当元素有序的时候,会一直递归,递归的深度过深,使递归速度较慢。
解决方式:选取一个中位数作为 基,下面以挖坑法为例:
public void digQuicklySort(int[] arr){
digQuicklySort(arr,0,arr.length-1);
}
privateintdigQuicklySort(int[] arr,int left,int right){
int root= findMid(arr, left, right);//找到中位数
swap(arr, root, left);//将这三个数 的中位数 ,放到最左边,作为基使用。
root = dig(arr,left,right);
digQuickluSort(arr,root+1,right);
digQuickluSort(arr,left,root+1);
return root;
}
//findMid并不是找这个数组的中位数,而是选择 left right left+right/2 这三个位置中间大小的数
private int findMid(int[] arr, int left, int right) {
int mid= (left + right) / 2;
//寻找左边为 left mid right 这三个数的下标
if (arr[right] > arr[left]) {
if (arr[mid] > arr[right]) return right;
else if (arr[mid] < arr[left]) return left;
else return mid;
} else {
if (arr[mid] > arr[left]) return left;
else if (arr[mid] < arr[right]) return right;
else return mid;
}
}优化2.减少递归
问题:递归过多会造成栈满
解决思路:叶子很多,假如到最后几层我们是不是就可以直接使用 插入排序,而且最后的元素也刚好基本趋于稳定
解决方式 :加一个if语句判断是继续递归还是直接插入排序,下面以挖坑法为例:
非递归实现快排
方法: 使用栈,方法基本参考非递归解决二叉树的问题
速度: 不用很多优化,但代码相对不好想。
优化??:可以尝试加入三数取中,插入排序的优化,参考3.1 3.2
代码:
public void quicklySortNoRecursion(int[] arr){
if (arr.length<=1) return;
Stack<Integer> stack = newStack<>();
int left=0,right = arr.length-1;
stack.push(left);
stack.push(right);
while(!stack.isEmpty()){
right = stack.pop();//记得一定要先弹出right 因为right是后放进去的
left = stack.pop();
int root= quicklyDig(arr,left,right);
if (root>left+1){//这个代表,左边至少有俩元素
stack.push(left);//注意这里也要放做再放右
stack.push(root-1);
}
if (root<right-1){//这个代表右边至少有两个元素
stack.push(root+1);
stack.push(right);
}
}
}
}归并排序
基本思想:先分解 后合并
常用场景:排序的数据量过大,内部排序的空间无法满足,这个时候就要使用外部排序。而归并排序就是最常用的外部排序
例子: 内存只有1G 但是需要排序的数据有100G
先把文件分成200份,每个512M,分别对512M排序,内存已经可以放下,任意排序都可以使用,进行2路归并,同时对200分有序文件做归并处理,最后结果就有序了
代码:
递归实现
public class MergeSort {
publicvoidmergeSort(int[] arr) {
mergeSort(arr, 0, arr.length - 1);
}
private void mergeSort(int[] arr, int left, int right) {
if (right <= left) return;
int mid= (right + left) / 2;
mergeSort(arr, left, mid);//分解左边
mergeSort(arr, mid + 1, right);//分解右边
merge(arr, left, right, mid);//合并
}
private void merge(int[] arr, int left, int right, int mid) {
int left1= left, right1 = mid;
int left2= mid + 1, right2 = right;
int[] arr2 = newint[right - left + 1];
intarr2Index=0;//arr2的坐标两个归并段 都有数据,那边的数据小那边先放
while (right1 >= left1 && right2 >= left2) {
if (arr[left1] <= arr[left2]) arr2[arr2Index++] = arr[left1++];
else arr2[arr2Index++] = arr[left2++];
}
//当走到这里的时候 说明 有个归并段 当中 没有了数据 ,拷贝另一半的全部 到tmpArr数组当中
while (right1 >= left1) arr2[arr2Index++] = arr[left1++];
while (right2 >= left2) arr2[arr2Index++] = arr[left2++];
for (inti= left; i <= right; i++) {
arr[i] = arr2[i - left];
}
}
}非递归实现
public void mergerNoSort(int[] arr) {
if (arr.length <= 1) return;
//假设每个元素都是一组数据intgap=1;//表示每组元素的个数
while (gap <= arr.length) {
for (inti=0; i < arr.length; i += 2 * gap) {
int left= i;
int right= i + 2 * gap - 1;
if (right > arr.length - 1) { right = arr.length - 1; }
int mid= left + gap-1;
if (mid>=arr.length) { mid = arr.length-1; }
merge(arr, i, right, mid);
}
gap *= 2;
}
}