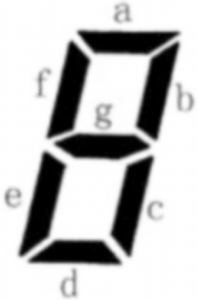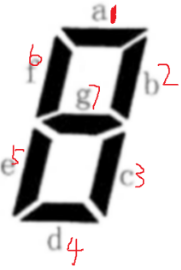并查集的入门与应用

news2024/9/27 23:24:30

目录

一、前言

二、并查集概念

1、并查集的初始化

2、并查集的合并

3、并查集的查找

4、初始化、查找、合并代码

5、复杂度

二、路径压缩

三、例题

1、蓝桥幼儿园（lanqiaoOJ题号1135）

2、合根植物（2017年决赛，lanqiaoOJ题号110）

3、修改数组（2019年省赛，lanqiaoOJ题号185）

（1）暴力法1

（2）暴力法2

（3）查重，hash或set()

（4）新思路——并查集

4、七段码（2020年省赛，lanqiaoOJ题号595，填空题）

一、前言

本文主要讲了并查集的概念、路径压缩，讨论了一题多解的思路和一些例题。

二、并查集概念

  • 并查集（Disjoint Set）：一种非常精巧而实用的数据结构。
  • 用于处理不相交集合的合并问题。
  • 经典应用：
  • 连通子图
  • 最小生成树 Kruskal 算法
  • 最近公共祖先

【场景1】

  • 有 n 个人，他们属于不同的帮派；
  • 已知这些人的关系，例如1号、2号是朋友，1号、3号 也是朋友，那么他们都属于一个帮派；
  • 问有多少帮派，每人属于哪个帮派。
  • 用并查集可以很简洁地表示这个关系。

【场景2】

有n个人一起吃饭，有些人互相认识。

认识的人想坐在一起，而不想跟陌生人坐。

例如A认识B，B认识C，那么A、B、C会坐在一张桌子上。

给出认识的人，问需要多少张桌子。

1、并查集的初始化

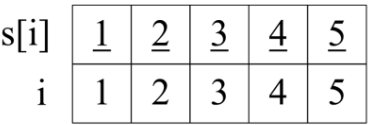
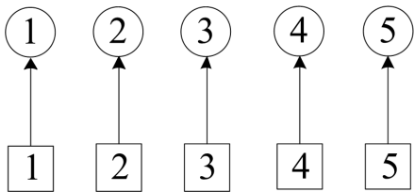
  • 定义 s[i] 是以结点 i 为元素的并查集。
  • 初始化：令 s[i]=i。(某人的号码是i，他属于帮派 s[i])

def init_set():     #初始化
    for i in range(N):
        a.append(i)

#s=list(range(N))   #init_set()可以简化为这一行

2、并查集的合并

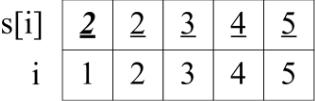
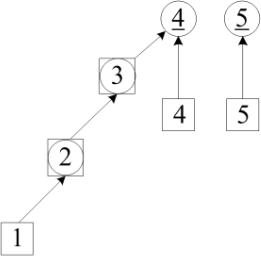
  • 例：加入第一个朋友关系 (1,2)。
  • 在并查集 s 中，把结点 1 合并到结点 2，也就是把结点 1 的集 1 改成结点 2 的集 2。

  • 加入第二个朋友关系 (1,3)
  • 查找结点1的集，是2，递归查找元素2的集是2；
  • 把元素2的集2合并到结点3的集3。
  • 此时，结点1、2、3都属于一个集。

  •  加入第三个朋友关系 (2,4)；

def merge_set(x,y):     #合并
    x=find_set(x)
    y=find_set(y)
    if x!=y:
        s[x]=s[y]

3、并查集的查找

查找元素的集，是一个递归的过程，直到元素的值和它的集相等，就找到了根结点的集。

def find_set(x):
    if x!=s[x]:
        return find_set(s[x])
    else:
        return x

这棵搜索树，可能很细长，复杂度 O(n)，变成了一个链表，出现了树的 “退化” 现象。

4、初始化、查找、合并代码

def init_set():     #初始化
    for i in range(N):
        a.append(i)

def find_set(x):
    if x!=s[x]:
        return find_set(s[x])
    else:
        return x

def merge_set(x,y):     #合并
    x=find_set(x)
    y=find_set(y)
    if x!=y:
        s[x]=s[y]

5、复杂度

  • 查找 find_set()、合并 merge_set() 的搜索深度是树的长度，复杂度都是 O(n)。
  • 性能差。
  • 能优化吗？
  • 目标：优化之后，复杂度 ≈ O(1)。

二、路径压缩

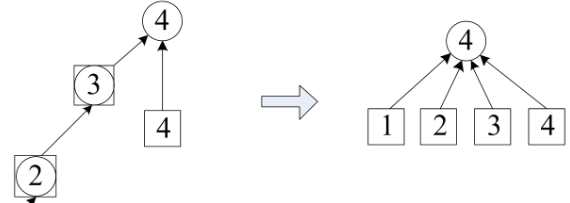
  • 查询程序 find_set()：沿着搜索路径找到根结点，这条路径可能很长。
  • 优化：沿路径返回时，顺便把 i 所属的集改成根结点。下次再搜，复杂度是 O(1）。

def find_set(x):    #有路径压缩优化的查询
    if x!=s[x]:
        s[x]=find_set(s[x])        #递归实现
    else:
        return x
  • 路径压缩：整个搜索路径上的元素，在递归过程中，从元素 i 到根结点的所有元素，它们所属的集都被改为根结点。
  • 路径压缩不仅优化了下次查询，而且也优化了合并，因为合并时也用到了查询。

三、例题

1、蓝桥幼儿园（lanqiaoOJ题号1135）

【题目描述】

蓝桥幼儿园的学生天真无邪，朋友的朋友就是自己的朋友。小明是蓝桥幼儿园的老师，这天他决定为学生们举办一个交友活动，活动规则如下：小明用红绳连接两名学生,被连中的两个学生将成为朋友。请你帮忙写程序判断某两个学生是否为朋友。

【输入描述】

第 1 行包含两个正整数 N,M，N 表示蓝桥幼儿园的学生数量，学生的编号分别为1- N。之后的第 2- M+1 行每行输入三个整数 op,x,y。如果 op=1，表示小明用红绳连接了学生 x 和学生 y。如果op=2，请你回答小明学生 x 和学生 y 是否为朋友。

1<=N,M<=2×10^5，1<=x,y<=N。

【输出描述】

对于每个 op=2 的输入，如果 x 和 y 是朋友，则输出一行 YES，否则输出一行 NO。

def init_set():
    for i in range(N):
        parent.append(i)

def find_set(x):
    if x!=parent[x]:
        parent[x]=find_set(parent[x])
    return parent[x]

def merge_set(x,y):
    x=find_set(x)
    y=find_set(y)
    if x!=y:
        parent[x]=parent[y]

n,m=map(int,input().split())
N=800_005
parent=[]    #并查集
init_set()
for i in range(m):
    op,x,y=map(int,input().split())
    if op==1:
        merge_set(x,y)
    if op==2:
        if find_set(x)==find_set(y):
            print("YES")
        else:
            print("NO")

2、合根植物（2017年决赛，lanqiaoOJ题号110）

【题目描述】

w 星球的一个种植园，被分成 m×n 个小格子（东西方向 m 行，南北方向 n 列）。每个格子里种了一株合根植物，这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

【输入格式】

第一行，两个整数 m,n，用空格分开，表示格子的行数、列数 (1<m,n<1000）。接下来一行，一个整数 k，表示下面有 k 行数据 (0<k<100000)。接下来 k 行，每行两个整数 a,b，表示编号为 a 的小格子和编号为 b 的小格子合根了。格子的编号一行一行，从上到下，从左到右编号。

【输出格式】

输出一个整数表示答案。

【常规做法】

  • 用并查集处理所有的合并；
  • 处理完后，检查所有 S[i] = i 的数量，也就是集等于自己的数量，就是答案。
  • 初始化时，假设所有植物都不合根，初始答案：ans = m×n。
  • 然后用并查集处理合根，合根一次，ans减一。
def find_set(x):
    if x!=parent[x]:
        parent[x]=find_set(parent[x])
    return parent[x]

def merge_set(x,y):
    x=find_set(x)
    y=find_set(y)
    if x==y:   # 同根
        return False
    parent[y]=parent[x]
    return True     # 合根一次

m,n=map(int,input().split())
k=int(input())
parent=list(range(m*n))
ans=m*n
for i in range(k):
    x,y=map(int,input().split())
    if merge_set(x,y):
        ans-=1
print(ans)

3、修改数组（2019年省赛，lanqiaoOJ题号185）

【题目描述】

给定一个长度为 N 的数组 A=[A1, A2,...,AN]，数组中有可能有重复出现的整数。现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A2,A3,...,AN。当修改 Ai 时，小明会检查 A 是否在 A1~Ai 中出现过。如果出现过，则小明会给 Ai 加上1：如果新的 Ai 仍在之前出现过，小明会持续给 Ai 加1，直到 Ai 没有在 A1~Ai 中出现过。当 AN 也经过上述修改之后，显然 A 数组中就没有重复的整数了。现在给定初始的 A 数组，请你计算出最终的 A 数组。

【输入】

第一行包含一个整数 N (1<=N<=100000)，第二行包含 N 个整数 A1, A2, ..., AN (1<=Ai<=1000000)。

【输出】

输出 N 个整数，依次是最终的 A1, A2, ..., AN

【输入示例】

5

2 1 1 3 4

【输出示例】

2 1 3 4 5

功能：把数组的数字转换为都不重复

数组 A = [A1, A2, ... ,AN]

依次修改 A2, A3, ..., AN

修改 Ai 时，检查 Ai 是否在 A1~Ai 中出现过

如果出现过，给Ai加上1；

如果新的 Ai 仍在之前出现过，持续给 Ai 加 1，直到 Ai 没有在 A1~Ai-1中出现过。

（1）暴力法1

1<=N<=100000

每读入一个新的数，就检查前面是否出现过，每一次需要检查前面所有的数。共有 n 个数，每个数检查 O(n) 次，总复杂度 O(n^3)，超时。

n=int(input())
a=[int(i) for i in input().split()]
for i in range(1,n):    #从第2个开始：a[1]
    for k in range(i):  #检查它前面的所有数，做k次
        for j in range(i):
            if a[i]==a[j]:
                a[i]+=1
for i in range(n):
    print(a[i],end=' ')
#for i in a:
#   print(i,end=' ')

（2）暴力法2

n=int(input())
a=[int(i) for i in input().split()]
for i in range(1,n):    #从第2个开始：a[1]
    for j in range(i):  #检查它前面的所有数
        while a[i] in a[0:i]:
            a[i]+=1
for i in range(n):
    print(a[i],end=' ')
#for i in a:
#   print(i,end=' ')

（3）查重，hash或set()

  • 改进，用hash。定义 vis[] 数组，vis[i] 表示数字 i 是否已经出现过。这样就不用检查前面所有的数了，基本上可以在 O(1) 的时间内定位到。
  • 或：直接用 set 判断是否重复，也是 O(1)。
n=int(input())
a=[int(i) for i in input().split()]
s=set()
for i in range(n):
    while a[i] in s:
        a[i]+=1
    s.add(a[i])
for i in range(n):
    print(a[i],end=' ')
#for i in a:
#   print(i,end=' ')

（4）新思路——并查集

本题特殊要求：“如果新的 Ai 仍在之前出现过，小明会持续给 Ai 加 1，直到 Ai 没有在 A1~Ai-1 中出现过。” 这导致在某些情况下，仍然需要大量的检查。

以 5 个 6 为例: A[]= {6,6, 6,6,6)。

第一次读 A[1]=6，设置 vis[6]=1。

第二次读 A[2]=6，先查到 vis[6]=1，则把 A[2] 加 1，变为 A[2]=7；再查 vis[7]=0，设置 vis[7]=1。检查了 2 次。

第三次读 A[3]=6，先查到 vis[6]=1，则把 A[3] 加 1 得 A[3]=7；再查到 vis[7]=1，再把 A[3] 加 1 得A[3]=8，设置 vis[8]=1；最后查 vis[8]=0，设置 vis[8]=1。

........

检查了 3 次。每次读一个数，仍需检查 O(n) 次，总复杂度 O(n^2)。

  • 本题用 Hash，在特殊情况下仍然需要大量的检查。
  • 问题出在 “持续给 Ai 加 1，直到 Ai 没有在 A1~Ai-1 中出现过”。
  • 也就是说，问题出在那些相同的数字上。当处理一个新的 Ai 时，需要检查所有与它相同的数字。
  • 如果把这些相同的数字看成一个集合，就能用并查集处理。

用并查集处理就非常巧妙了！

用并查集 s[i] 表示访问到 i 这个数时应该将它换成的数字。

以 A[]= {6,6,6,6,6) 为例。初始化 set[i]=i

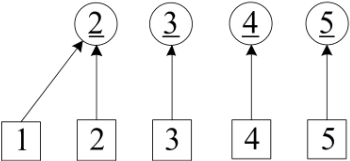
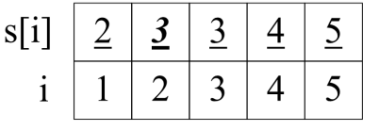
图(1)读第一个数 A[0]=6。 6 的集 set[6]=6。紧接着更新 set[6]=set[7]=7，作用是后面再读到某个A[k] =6时，可以直接赋值A[k]=set[6] =7。

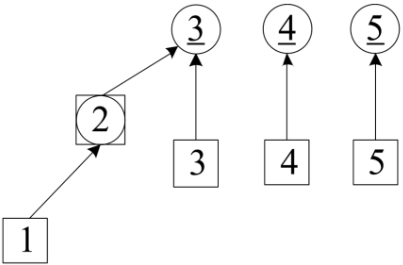
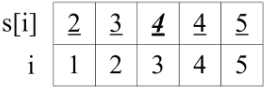
图(2)读第二个数 A[1]=6。 6 的集 set[6]=7，更新 A[1]=7。紧接着更新 set[7]=set[8]=8。如果后面再读到 A[k]=6或7 时，可以直接赋值 A[k]=set[6]=8 或者 A[k]=set[7]=8.

  • 只用到并查集的查询，没用到合并。
  • 必须是“路径压缩”优化的，才能加快查询速度。没有路径压缩的并查集，仍然超时。
  • 复杂度O(n)

上面的处理还是很值得思考一下的。

def find_set(x):
    if x!=parent[x]:
        parent[x]=find_set(parent[x])
    return parent[x]
N=1000002
parent=list(range(N))
n=int(input())
a=[int(i) for i in input().split()]
for i in range(n):
    root=find_set(a[i])
    a[i]=root
    parent[root]=find_set(root+1)   #加一
for i in a:
    print(i,end=' ')

4、七段码（2020年省赛，lanqiaoOJ题号595，填空题）

【问题描述】

七段数码管，一共有 7 个发光二极管，问能表示多少种不同的字符，要求发光的二极管是相连的。

  • 标准思路：“灯的组合+连通性检查”
  • 编码：“DFS+并查集”

a b c d e f g

字符用数字表示

1 2 3 4 5 6 7

 

N=10
e=[[0]*N for i in range(N)]
s=[0]*N
vis=[0]*N
ans=0
e[1][2]=e[1][6]=1
e[2][1]=e[2][3]=e[2][7]=1
e[3][2]=e[3][4]=e[3][7]=1
e[4][3]=e[4][5]=1
e[5][4]=e[5][6]=e[5][7]=1
e[6][1]=e[6][5]=e[6][7]=1
e[7][2]=e[7][3]=e[7][5]=e[7][6]=1
dfs(1)      #从第一个灯开始深搜
print(ans)
  • 灯的所有组合用 DFS 得到，用 “自写组合算法”。
  • 选或不选第 k 个灯，就实现了各种组合。
  • check() 函数判断一种组合的连通性。
def dfs(k):       #深搜到第k个灯
    if k==8:
        check()     #检查连通性
    else:
        vis[k]=1    #点亮这个灯
        dfs(k+1)    #继续搜下一个灯
        vis[k]=0    #关闭这个灯
        dfs(k+1)    #继续搜下一个灯
  • check() 函数判断一种组合的连通性。
  • 连通性检查用并查集。
  • 判断灯 i、j 都在组合中且相连，那么合并到一个并查集。
  • flag=1，表示这个组合中的所有灯都合并到了同一个并查集，说明它们是连通的。
def check():
    global ans
    init()
    for i in range(1,8):
        for j in range(1,8):
            if e[i][j]==1 and vis[i]==1 and vis[j]==1:
                merge_set(i,j)
    flag=0
    for j in range(1,8):
        if vis[j]==1 and s[j]==j:
            flag+=1
    if flag==1:
        ans+=1

【完整代码】

def init():
    for i in range(N):
        s[i]=i
def find_set(x):
    if x!=s[x]:
        s[x]=find_set(s[x])
    return s[x]
def merge_set(x,y):
    x=find_set(x)
    y=find_set(y)
    if x!=y:
        s[x]=s[y]

def check():
    global ans
    init()
    for i in range(1,8):
        for j in range(1,8):
            if e[i][j]==1 and vis[i]==1 and vis[j]==1:
                merge_set(i,j)
    flag=0
    for j in range(1,8):
        if vis[j]==1 and s[j]==j:
            flag+=1
    if flag==1:
        ans+=1

def dfs(k):       #深搜到第k个灯
    if k==8:
        check()     #检查连通性
    else:
        vis[k]=1    #点亮这个灯
        dfs(k+1)    #继续搜下一个灯
        vis[k]=0    #关闭这个灯
        dfs(k+1)    #继续搜下一个灯

N=10
e=[[0]*N for i in range(N)]
s=[0]*N
vis=[0]*N
ans=0
e[1][2]=e[1][6]=1
e[2][1]=e[2][3]=e[2][7]=1
e[3][2]=e[3][4]=e[3][7]=1
e[4][3]=e[4][5]=1
e[5][4]=e[5][6]=e[5][7]=1
e[6][1]=e[6][5]=e[6][7]=1
e[7][2]=e[7][3]=e[7][5]=e[7][6]=1
dfs(1)      #从第一个灯开始深搜
print(ans)

以上，并查集的入门与应用

祝好

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/175265.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SQL注入篇 - 布尔盲注及延时注入

SQL注入篇 - 布尔盲注及延时注入

数据来源 盲注 什么是盲注&#xff1a; 布尔盲注原理 布尔盲注流程 手工盲注思路&#xff08;以下的文章参考&#xff1a;DVWA-sql注入&#xff08;盲注&#xff09; - N0r4h - 博客园&#xff09; 手工盲注的过程&#xff0c;就像你与一个机器人聊天&#xff0c;这个机器人知…
阅读更多...
DGSEA | GSEA做完了不要停，再继续比较一下有意义的通路吧！~

DGSEA | GSEA做完了不要停，再继续比较一下有意义的通路吧！~

1写在前面 GSEA大家都会用了&#xff0c;但GSEA也有它自己的缺点&#xff0c;就是不能比较两个基因集或通路的富集情况。&#x1f912; 今天介绍一个Differential Gene Set Enrichment Analysis (DGSEA)&#xff0c;可以量化两个基因集的相对富集程度。&#x1f609; 2用到的包…
阅读更多...
Java中的位运算及其常见的应用

Java中的位运算及其常见的应用

文章目录1、位运算1.1 原码、反码、补码1.2 位运算符2、位运算的应用2.1 取模运算2.2 奇偶性判断2.3 交换变量的值2.4 加法运算1、位运算 1.1 原码、反码、补码 计算机中所有数据的存储和运算都是以二进制补码的形式进行的。a —> 97&#xff0c;A —> 65&#xff0c;‘…
阅读更多...
深入学习Vue.js（十二）编译器

深入学习Vue.js（十二）编译器

模板DSL的编译器 1.编译器概述 编译器实际上是一段程序&#xff0c;他用来将一种语言A翻译为另一种语言B。其中&#xff0c;A被称为源代码&#xff0c;B被称为目标代码。编译器将源代码翻译为目标代码的过程被称为编译。完整的编译过程通常包含词法分析、语法分析、语义分析、…
阅读更多...
软件测试——测试用例

软件测试——测试用例

作者&#xff1a;~小明学编程 文章专栏&#xff1a;测试开发 格言&#xff1a;热爱编程的&#xff0c;终将被编程所厚爱。 目录 测试用例的设计方法 等价类 边界值 错误猜测法 判定表法&#xff08;使用于关系组合&#xff09; 设计步骤 具体例子 正交法 场景设计法…
阅读更多...
Redis相关简介

Redis相关简介

1. Redis 简介 在这个部分&#xff0c;我们将学习以下3个部分的内容&#xff0c;分别是&#xff1a; ◆ Redis 简介&#xff08;NoSQL概念、Redis概念&#xff09; ◆ Redis 的下载与安装 ◆ Redis 的基本操作 1.1 NoSQL概念 1.1.1 问题现象 在讲解NoSQL的概念之前呢&am…
阅读更多...
8. R语言画：散点图、直方图、条形图、箱线图、小提琴图、韦恩图

8. R语言画：散点图、直方图、条形图、箱线图、小提琴图、韦恩图

b站课程视频链接&#xff1a; https://www.bilibili.com/video/BV19x411X7C6?p1 腾讯课堂(最新&#xff0c;但是要花钱&#xff0c;我花99&#x1f622;&#x1f622;元买了&#xff0c;感觉讲的没问题&#xff0c;就是知识点结构有点乱&#xff0c;有点废话&#xff09;&…
阅读更多...
九大数据分析方法-综合型分析方法以及如何使用这九大分析方法

九大数据分析方法-综合型分析方法以及如何使用这九大分析方法

文章目录3 综合型分析方法3.1 相关性分析法3.1.1 直接相关3.1.2 间接相关3.2标签分析法3.3 MECE法4 如何使用九大方法本文来源&#xff0c;为接地气的陈老师的知识星球&#xff0c;以及付同学的观看笔记。3 综合型分析方法 3.1 相关性分析法 相关性分析法&#xff1a;寻找指标…
阅读更多...
ROS2机器人编程简述humble-第二章-Executors .3.5

ROS2机器人编程简述humble-第二章-Executors .3.5

ROS2机器人编程简述humble-第二章-Parameters .3.4由于ROS2中的节点是C对象&#xff0c;因此一个进程可以有多个节点。事实上&#xff0c;在许多情况下&#xff0c;这样做是非常有益的&#xff0c;因为当通信处于同一进程中时&#xff0c;可以通过使用共享内存策略来加速通信。…
阅读更多...
freeglut 在mfc 下的编译

freeglut 在mfc 下的编译

freeglut 是OpenGL Utility Toolkit (GLUT) library 的替代版本&#xff0c;glut 应用广阔&#xff0c;但比较陈旧&#xff0c;很久没有更新。 我原来的opengl 用的是glut&#xff0c; 想更新到64位版本&#xff0c;怎么也找不到合适的下载。最后找到完全替代版本freeglut。fre…
阅读更多...
【Linux】线程概念 | 互斥

【Linux】线程概念 | 互斥

千呼万唤始出来&#xff0c;终于到多线程方面的学习了&#xff01; 所用系统Centos7.6 本文的源码&#x1f449;【传送门】 最近主要是在我的hexo个人博客上更新&#xff0c;csdn的更新会滞后 文章目录1.线程的概念1.1 执行流1.2 线程创建时做了什么&#xff1f;1.3 内核源码中…
阅读更多...
每刻和金蝶云星空接口打通对接实战

每刻和金蝶云星空接口打通对接实战

接通系统&#xff1a;每刻3000中大型企业在用&#xff0c;新一代业财税一体化解决方案提供商。旗下拥有每刻报销、每刻档案、每刻云票、每刻财务共享云平台等&#xff0c;助力企业实现财务数字化转型。对接系统&#xff1a;金蝶云星空金蝶K/3Cloud结合当今先进管理理论和数十万…
阅读更多...
算法刷题打卡第72天：最少侧跳次数

算法刷题打卡第72天：最少侧跳次数

最少侧跳次数 难度&#xff1a;中等 给你一个长度为 n 的 3 跑道道路 &#xff0c;它总共包含 n 1 个 点 &#xff0c;编号为 0 到 n 。一只青蛙从 0 号点第二条跑道 出发 &#xff0c;它想要跳到点 n 处。然而道路上可能有一些障碍。 给你一个长度为 n 1 的数组 obstacle…
阅读更多...
Cheat Engine7.4 训练教程（非常详细）

Cheat Engine7.4 训练教程（非常详细）

目录 一.CE是干什么的&#xff1f; 二.怎么获得&#xff1f; 三.训练教程 步骤 1: 加载进程 步骤 2: 精确值扫描 步骤 3: 未知的初始值 步骤 4: 浮点数 步骤 5: 代码查找 步骤 6: 指针 步骤 7: 代码注入 步骤 8: 多级指针 提示&#xff1a;这篇文章不是一天写完的&a…
阅读更多...
设计模式-建造者模式

设计模式-建造者模式

1.概述 将一个复杂对象的构建与表示分离&#xff0c;使得同样的构建过程可以创建不同的表示。 分离了部件的构造(由Builder来负责)和装配(由Director负责)。 从而可以构造出复杂的对象。这个模式适用于&#xff1a;某个对象的构建过程复杂的情况。由于实现了构建和装配的解耦…
阅读更多...
基于ffmpeg的视频处理与MPEG的压缩试验(下载安装使用全流程)

基于ffmpeg的视频处理与MPEG的压缩试验(下载安装使用全流程)

基于ffmpeg的视频处理与MPEG的压缩试验ffmpeg介绍与基础知识对提取到的图像进行处理RGB并转化为YUV对YUV进行DCT变换对每个8*8的图像块进行进行量化操作ffmpeg介绍与基础知识 ffmpeg是视频和图像处理的工具包&#xff0c;它的下载网址是https://ffmpeg.org/download.html。页面…
阅读更多...
MySQL高级

MySQL高级

存储引擎 MySQL体系结构&#xff1a; 存储引擎就是存储数据、建立索引、更新/查询数据等技术的实现方式。存储引擎是基于表而不是基于库的&#xff0c;所以存储引擎也可以被称为表引擎。 默认存储引擎是InnoDB。 相关操作&#xff1a; -- 查询建表语句 show create table ac…
阅读更多...
Python量化交易07——散户反买策略

Python量化交易07——散户反买策略

参考来源&#xff1a;b站up 邢不行 我们都知道在A股&#xff0c;散户一直是最大的韭菜贡献组群。散户买入多的个股&#xff0c;大概率可能跌的很惨&#xff0c;散户卖出多的股票&#xff0c;大概率会涨。 跟着北向资金买能赚钱&#xff0c;那么跟着散户反买&#xff0c;是不是…
阅读更多...
宝塔面板部署Django项目教程(手把手)

宝塔面板部署Django项目教程(手把手)

一、测试环境 系统&#xff1a;centos 7.9 CPU&#xff1a;1核 内存&#xff1a;2G 二、安装宝塔面板 输入命令&#xff1a; yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh ed8484bec 后面会…
阅读更多...
【nvidia CUDA 高级编程】使用cub库优化分布式计算下的原子操作

【nvidia CUDA 高级编程】使用cub库优化分布式计算下的原子操作

博主未授权任何人或组织机构转载博主任何原创文章&#xff0c;感谢各位对原创的支持&#xff01; 博主链接 本人就职于国际知名终端厂商&#xff0c;负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作&#xff0c;目前牵头6G算力网络技术标准研究。 博客…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023