题目链接

4797. 移动棋子
4798. 打怪兽
4799. 最远距离

题目描述

4797. 移动棋子

给定一个 5 行 5 列的方格矩阵，其中一个方格中有一个棋子。

现在，我们希望将棋子移动至矩阵的最中心方格中，即将其移动至矩阵的第 3行第 3列方格中。

每次移动可以将棋子沿上、下、左、右任一方向移动一格距离，前提是不能移出矩阵。

请你计算，为了将棋子移动至矩阵的最中心方格中，所需要的最少移动次数。

如果棋子一开始就在最中心方格中，则无需移动。

输入格式

输入共 5行，每行包含 5个整数，其中第 i 行第 j 列的整数表示第 i 行第 j 列方格的状态，如果为 0，则表示该方格中没有棋子，如果为 1，则表示该方格中有棋子。

保证只有一个方格中有棋子。

输出格式

一个整数，表示所需要的最少移动次数。

数据范围

所有测试点满足，输入恰好包含 24 个 0 和 1 个 1。

输入样例1：

0 0 0 0 0
0 0 0 0 1
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0

输出样例1：

3

输入样例2：

0 0 0 0 0
0 0 0 0 0
0 1 0 0 0
0 0 0 0 0
0 0 0 0 0

输出样例2：

1

输入样例3：

0 0 0 0 0
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0

输出样例3：

0

分析：
根据题意 直接返回 值为1的坐标(x,y) 与 中心点(3,3) 的 曼哈顿距离。

时间复杂度：$O(1)$

代码：

#include<iostream>
#include<cmath>
using namespace std;

const int N = 10;
int a[N][N];

int main(){
    int x = -1,y = -1;
    for(int i = 1;i <= 5;i++){
        for(int j = 1;j <= 5;j++){
            cin>>a[i][j];
            //如果 a[i][j] == 1 则记录下 下标 i 和 j
            if(a[i][j]){
                x = i;y = j;
            }
        }
    }
    cout<<abs(x-3) + abs(y-3)<<endl;
    return 0;
}

4798. 打怪兽

有 n个怪兽（编号 $1\sim n$），其中第 $i$个怪兽的防御值为 $a_i$。

你是一个魔法师，初始时拥有 $m$ 点法力值。

当你的法力值大于 0 时，你可以对怪兽发动攻击，每一次攻击具体为：

• 任意选择 1∼2个怪兽，并消耗 x 点法力值（x 可以是一个不超过你当前法力值的任意正整数），对每个所选怪兽发动一次伤害为 x的攻击。
• 对于受到攻击的怪兽，如果其防御值小于或等于 x，则会被你消灭。否则，它将免疫此次攻击，不受任何影响。

请你确定最大的整数 k，满足：通过合理安排攻击，可以将第 $1\sim k$ 个怪兽全部消灭。

输入格式

第一行包含整数 $n,m$。

第二行包含 $n$个整数 $a_1,a_2,\dots ,a_n$。

输出格式

一个整数，表示最大的整数 k。

数据范围

所有测试点满足

• $1\le n\le 1000$
• $1\le m\le 10^9$
• $1\le a_i\le m$

输入样例1：

5 7
2 3 5 4 1

输出样例1：

3

输入样例2：

10 10
9 1 1 1 1 1 1 1 1 1

输出样例2：

4

输入样例3：

5 10
3 1 4 2 4

输出样例3：

5

分析：

我们可以通过 二分 的方式不断地来逼近 k。

此外我们还需要一个 $check()$ 函数，来判断我们当前二分的 $mid$ 是否是符合要求的。如果 $check(mid)==true$ 说明满足要求，那么将 左区间 $left$ 更新为 $mid$；否则说明选择的 $mid$ 太大了，所以更新 右区间 $right$ 为 $mid-1$。

$check()$ 函数内部：

• 由于是任意选择的，所以必然将数组排好序从小大大选，花费的法力值更少（因因为可能要二分很多次，所以这里直接新建一个原数组的副本($1-mid$)）。
• 我们定义 $f(i)$ 为消灭前 i 个怪兽，所需要的最少法力值。
• • 状态转移：$f(i)=min(f(i-1)+a[i],f(i-2)+max(a[i-1],a[i]))$
• 最后只需要判断 $f(mid)<=m$ 即可。

时间复杂度：$O(n\ast lo{g}^2(n))$

代码：

#include<iostream>
#include<vector>
#include<algorithm>
#include<cstring>
using namespace std;
using LL = long long;

const int N = 1010;
int a[N];
LL f[N];
int n,m;



bool check(int k){
    //每次要将 f 置为0
    memset(f,0,sizeof f);
    vector<int> arr(k+1);
    //赋值 a[1] ~ a[k] 到 arr副本中
    for(int i = 1;i <= k;i++) arr[i] = a[i];
    
    sort(arr.begin(),arr.end());
    
    f[1] = arr[1];
    f[2] = max(arr[1],arr[2]);
    
    for(int i = 3;i <= k;i++){
        f[i] = min(f[i-2]+max(arr[i-1],arr[i]),f[i-1]+arr[i]);
    }
    
    return f[k] <= m;
}



int main(){
    cin>>n>>m;
    for(int i = 1;i <= n;i++) cin>>a[i];
    
    //二分
    int l = 1,r = n;
    while(l<r){
        //因为是 l = mid 所以二分的时候需要加1 避免边界问题
        int mid = (l + r + 1) >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    
    
    cout<<l<<endl;
    return 0;
}

4799. 最远距离

我们规定，如果一个无向连通图满足去掉其中的任意一条边都会使得该图变得不连通，则称该图为有效无向连通图。

给定一个 $n$个点 $m$ 条边的有效无向连通图，点的编号为 $1\sim n$，所有边的长度均为 1。

两点之间的距离定义为两点之间的最短距离。

请你计算，给定图中距离最远的两个点之间的距离。

输入格式

第一行包含两个整数 $n,m$。

接下来 $m$ 行，每行包含两个整数 $a,b$，表示点 $a$和点 $b$ 之间存在一条无向边。

输出格式

一个整数，表示给定图中距离最远的两个点之间的距离。

数据范围

所有测试点满足

• $1\le n,m\le 10^5$
• $1\le a,b\le n$
• $a\ne b$

输入样例1：

4 3
1 2
1 3
1 4

输出样例1：

2

输入样例2：

5 4
1 2
2 3
3 4
3 5

输出样例2：

3

分析：

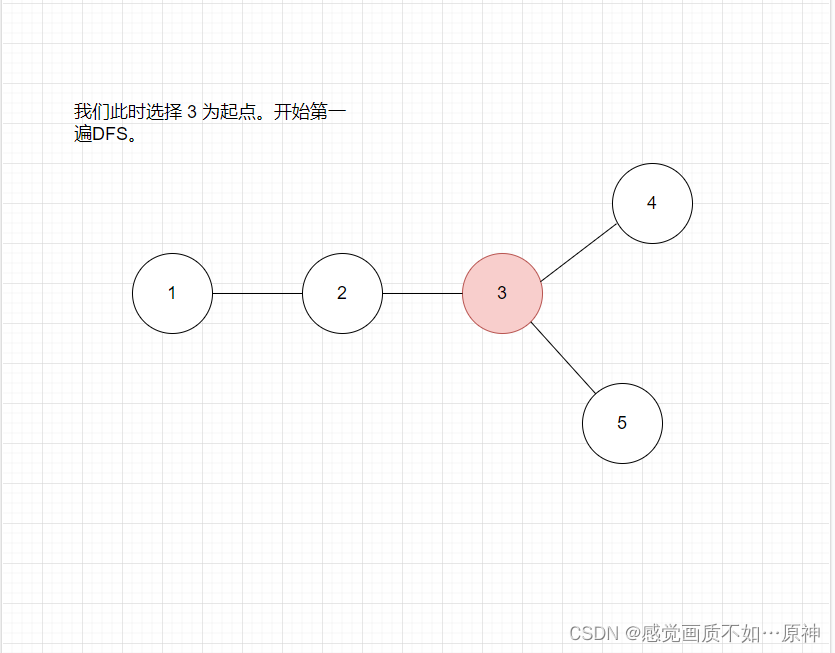
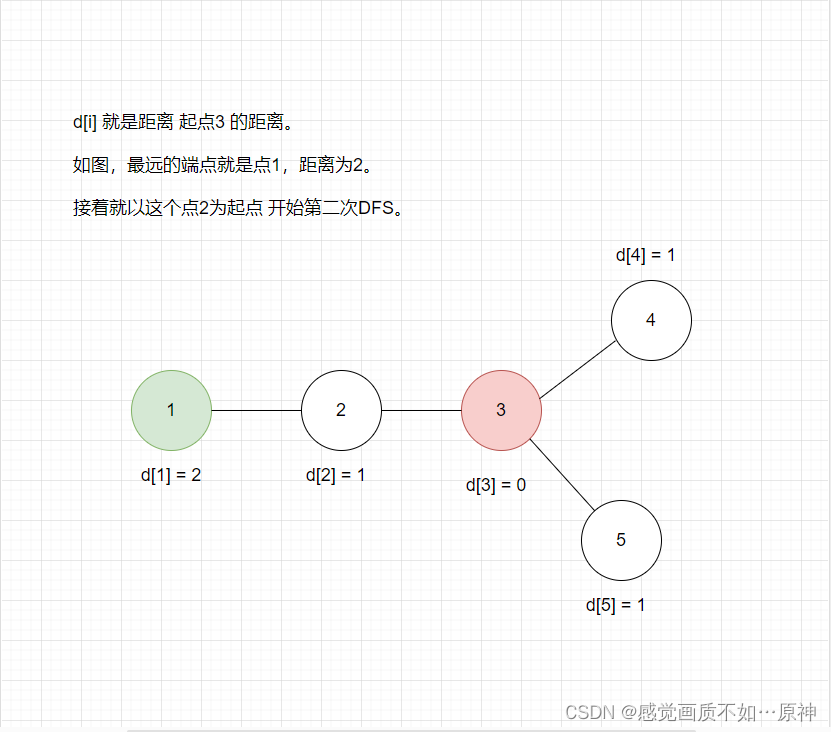
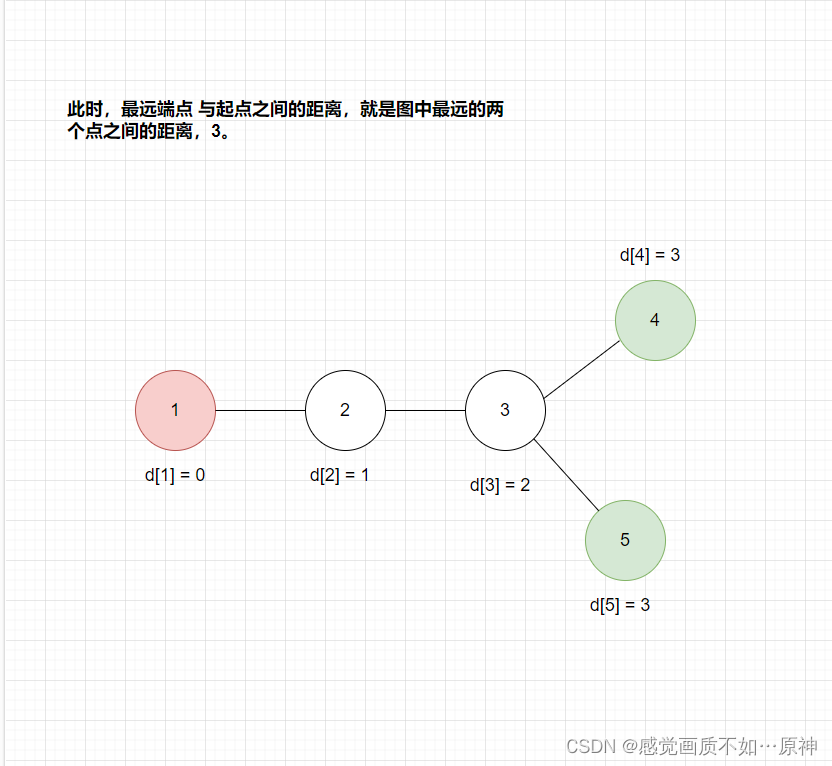
本题可以通过 两遍DFS 解决。

我们先挑选 任意一个点 $u$ 出发，第一遍DFS 求出距离 $u$ 最远的点 $v$。
第二遍DFS求出 $v$ 的最远端点 $e$，此时 $v$ 和 $e$ 之间就是最长的距离。

时间复杂度：$O(n)$

代码：

#include<iostream>
#include<vector>
using namespace std;

const int N = 1e5+10;

int n,m, c, d[N];
vector<int> E[N];

void dfs(int u, int fa) {
  for (int v : E[u]) {
    if (v == fa) continue;
    d[v] = d[u] + 1;
    
    if (d[v] > d[c]) c = v;
    
    dfs(v, u);
  }
}

int main() {
  scanf("%d%d", &n,&m);
  for (int i = 1; i <= m; i++) {
    int u, v;
    scanf("%d %d", &u, &v);
    //因为是无向图，要建两条边
    E[u].push_back(v), E[v].push_back(u);
  }
  //从 1点 开始dfs
  dfs(1, -1);
  
  //此时的 c点 就是距离 1点最远的点
  d[c] = 0;
  
  //再以c点为起点，求得的最长距离 d[c] 就是答案
  dfs(c, -1);
  
  
  printf("%d\n", d[c]);
  return 0;
}