题目如下：

在这里插入图片描述

示例1

输入

1 0 0 1

输出

0 0

说明

输出1 1也是可以的。

思路 or 题解：

我们可以迅速找到 $C$ 有两个位置满足题意，但 $C$ 的坐标不一定是整数，我们需要 $c h ec k$
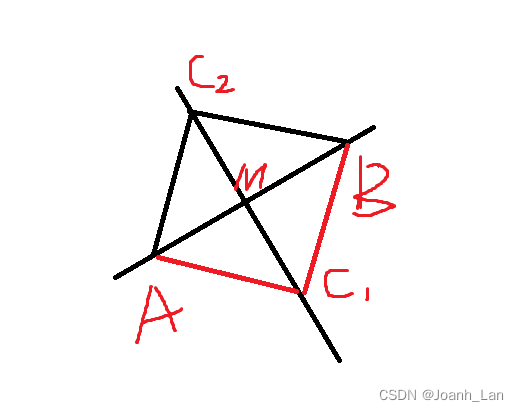
在这里插入图片描述
$M$ 是 $A B$ 的中点
我们可以求出来 $\overrightarrow{AM}$ , $\overrightarrow{MC_1}$ , $\overrightarrow{MC_2}$
通过向量我们可以求出 $C_1, C_2$ 的坐标，最后 $c h ec k$ 一下就行了

注意：

为了在计算中不出现分数，我们可以把坐标均乘以 $2$ , 最后答案坐标除以 $2$ 即可。

AC 代码如下：

/*
Make it simple and keep self stupid
author：Joanh_Lan
*/
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <numeric>
#include <cstring>
#include <cmath>
#include <map>
#include <unordered_map>
#include <bitset>
#include <set>
#include <random>
#include <ctime>
#include <queue>
#include <stack>
#include <climits>
#define buff                     \
    ios::sync_with_stdio(false); \
    cin.tie(0);
#define int long long
#define ll long long
#define PII pair<int, int>
#define px first
#define py second
typedef std::mt19937 Random_mt19937;
Random_mt19937 rnd(time(0));
using namespace std;
const int mod = 1e9 + 7;
const int inf = 2147483647;
const int N = 100009;
//int Mod(int a,int mod){return (a%mod+mod)%mod;}
//int lowbit(int x){return x&-x;}//最低位1及其后面的0构成的数值
//int qmi(int a, int k, int p){int res = 1 % p;while (k){if (k & 1) res = Mod(res * a , p);a = Mod(a * a , p);k >>= 1;}return res;}
//int inv(int a,int mod){return qmi(a,mod-2,mod);}
//int lcm(int a,int b){return a*b/__gcd(a,b);}
void solve()
{
    int x1, x2, y1, y2;
    cin >> x1 >> y1 >> x2 >> y2;
    x1 *= 2, x2 *= 2, y1 *= 2, y2 *= 2;
    int mx = (x1 + x2) / 2ll, my = (y1 + y2) / 2ll;
    int detla_x = mx - x1, detla_y = my - y1;
    if ((detla_y + mx) % 2ll == 0 && (-detla_x + my) % 2ll == 0)
        cout << (detla_y + mx) / 2ll << ' ' << (-detla_x + my) / 2ll << '\n';
    else if((-detla_y + mx) == 0 && (detla_x + my) % 2 == 0)
        cout << (-detla_y + mx) / 2ll << ' ' << (detla_x + my) / 2ll << '\n';
    else
        cout << "No Answer!\n";
}
signed main()
{
    buff;
    solve();
}