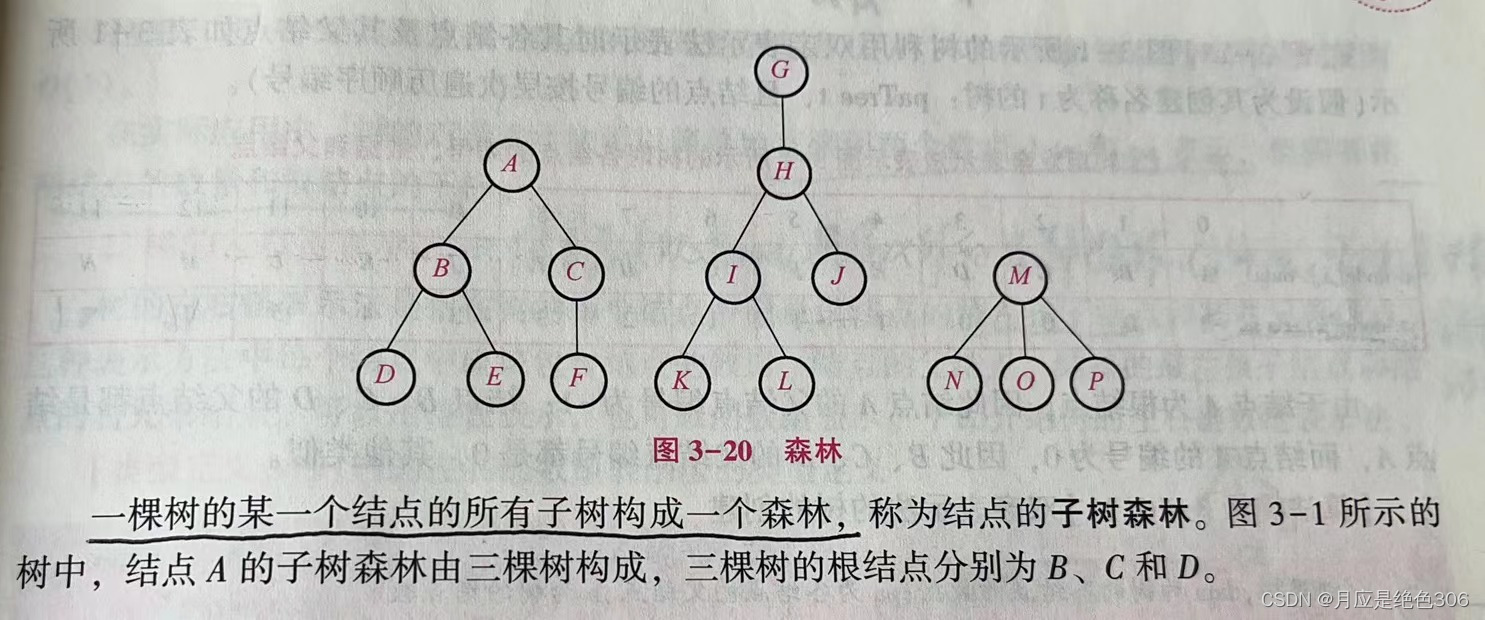
森林的定义 

森林是由多颗互不相交的树所构成的树的集合，即森林包含多棵树，每一棵树都有自己的根结点。一棵树也可以看成森林。

 

树的表示及基本操作 

1.树（一般树）的表示方法

1.1树的双亲表示法

树的双亲表示法是将树的各个节点存储在一个数组中，每一个结点都与数组的下标唯一对应，在每个结点中记录其父结点的下标，根结点的父结点为-1。

（最左孩子结点:一个结点的孩子结点中位于最左边的孩子结点）

在实际应用中，树的双亲表示法可以简单地直接用两个数组data和pa表示，但需要指明结点的数量和根结点的下标。

注意：在树的双亲表示法中必须严格按照层次遍历的顺序进行编号。

#include<iostream>
using namespace std;
constexpr auto N = 30;
typedef char datatype;
struct paNode {
	int pa; //父结点的下标
	datatype data;
	paNode() :pa(-1) {};
};
typedef struct {
	paNode tree[N];
	int n;	//树中节点的数量
	int root;  //树的根结点下标
}paTree;

//双亲表示法的树的创建
paTree create_paTree(datatype data[N], int pa[N], int n) {
	paTree t;
	t.n = n;
	for (int i = 0; i < n; i++) {
		t.tree[i].pa = pa[i], t.tree[i].data = data[i];
		if (pa[i] == -1)
			t.root = i;
	}
}

//求双亲表示法的树中某个结点的最左孩子结点和右兄弟节点
//求树t中结点cur的最左孩子结点，结果作为返回值。如果cur为叶结点，则返回-1
int lm_child(paTree t, int cur) {
	for(int i = cur + 1; i < t.n; i++) {
		if (t.tree[i].pa == cur)
			return i; //cur的最左孩子结点为i
	}
	return -1;
}

//求树t中结点cur的右兄弟结点，结果作为返回值。如果cur没有右兄弟结点，则返回-1
int r_brother(paTree t, int cur) {
	if (cur < t.n && t.tree[cur + 1].pa == t.tree[cur].pa) {
		return cur + 1;
	}
	return -1;
}

int main() {

}

1.2树的左右链表示法

树的左右链表示法是指在树的每个结点中记录该结点的最左孩子结点和其右兄弟结点。这种表示方法中每个结点中应该包含节点的数据、结点的父节点、结点的最左孩子结点和结点的右兄弟节点。可以用链表表示，也可以用数组表示。

#include<iostream>
using namespace std;
constexpr auto N = 30;
typedef char datatype;

struct lrbNode {
	datatype data;
	int pa;
	int lmc; //最左孩子结点
	int rb; //右兄弟结点
	lrbNode() :lmc(-1), rb(-1) {};
};
typedef struct {
	lrbNode tree[N]; //结点表
	int n; //树的节点总数
	int root;//树的根结点下标
}lrbTree;

//树的孩子列表数组表示法的基本操作
//创建数，data为树的各结点的数据，pa为各结点的父节点，n为树的结点数
lrbTree create_lrbTree(datatype data[], int pa[], int n) {
	lrbTree t;
	t.n = n;
	for (int i = 0; i < n; i++) {
		t.tree[i].data = data[i];
		if (pa[i] == -1) t.root = i; //指定树的父节点
		else {
			t.tree[i].pa = pa[i];//指定结点i的父节点
			if (t.tree[pa[i]].lmc == -1)t.tree[pa[i]].lmc = i; //i为其父节点的第一个孩子结点
			else {
				t.tree[i - 1].rb = i; //i有左兄弟结点i-1，i即为i-1的右兄弟节点
			}
		}
	}
	return t;
}

//求树t中结点cur的最左孩子结点的下标，结果作为返回值
int lm_child(lrbTree t,int cur) {
	return t.tree[cur].lmc;
}

//求树t中结点cur的右兄弟的下标，结果作为函数返回值
int r_brother(lrbTree t, int cur) {
	return t.tree[cur].rb;
}

int main() {

}

树和森林的遍历

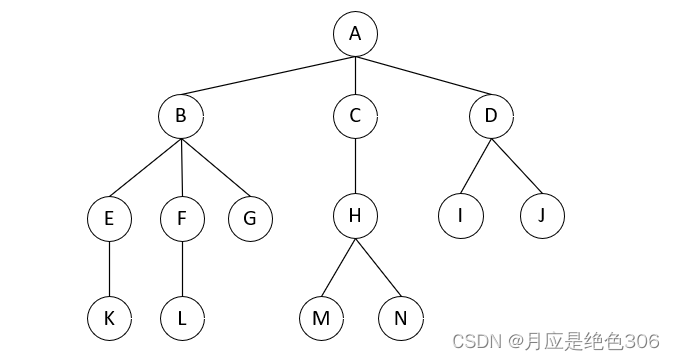
树的遍历 

 

#include<iostream>
using namespace std;
constexpr auto N = 30;
typedef char datatype;

struct lrbNode {
	datatype data;
	int pa;
	int lmc; //最左孩子结点
	int rb; //右兄弟结点
	lrbNode() :lmc(-1), rb(-1) {};
};
typedef struct {
	lrbNode tree[N]; //结点表
	int n; //树的节点总数
	int root;//树的根结点下标
}lrbTree;

//树的孩子列表数组表示法的基本操作
//创建数，data为树的各结点的数据，pa为各结点的父节点，n为树的结点数
lrbTree create_lrbTree(datatype data[], int pa[], int n) {
	lrbTree t;
	t.n = n;
	for (int i = 0; i < n; i++) {
		t.tree[i].data = data[i];
		if (pa[i] == -1) t.root = i; //指定树的父节点
		else {
			t.tree[i].pa = pa[i];//指定结点i的父节点
			if (t.tree[pa[i]].lmc == -1)t.tree[pa[i]].lmc = i; //i为其父节点的第一个孩子结点
			else {
				t.tree[i - 1].rb = i; //i有左兄弟结点i-1，i即为i-1的右兄弟节点
			}
		}
	}
	return t;
}

//求树t中结点cur的最左孩子结点的下标，结果作为返回值
int lm_child(lrbTree t, int cur) {
	return t.tree[cur].lmc;
}

//求树t中结点cur的右兄弟的下标，结果作为函数返回值
int r_brother(lrbTree t, int cur) {
	return t.tree[cur].rb;
}

//树的三种遍历方法
//对树t进行先根遍历，rt为当前子树的根结点
void preOrder(lrbTree t, int rt) {
	if (rt == -1)return;
	cout << t.tree[rt].data; //先访问根结点
	int cur = lm_child(t, rt); //根结点的最左孩子结点
	while (cur != -1) { //从树t的最左子树开始，依次先根遍历t的子树森林
		preOrder(t, cur);
		cur = r_brother(t, cur); //结点cur的右兄弟结点
	}
}

//对树t进行中根遍历，rt为当前子树的根结点
void midOrder(lrbTree t, int rt) {
	if (rt == -1)return;
	int cur = lm_child(t, rt); //根结点的最左孩子结点
	midOrder(t, cur);//中根遍历t的最左子树
	cout << t.tree[rt].data; //在t的最左子树遍历结束后访问根结点
	while (cur != -1) { //根结点的最左孩子结点
		cur = r_brother(t, cur);//结点cur的右兄弟结点
		midOrder(t, cur);
	}
}

//对树t进行后根遍历，rt为当前子树的根结点
void postOrder(lrbTree t, int rt) {
	if (rt == -1) return;
	int cur = lm_child(t, rt);  //根结点的最左孩子结点
	while (cur != -1) { //从t的最左孩子结点出发，依次后根遍历t的子树森林
		postOrder(t, cur);
		cur = r_brother(t, cur);  //结点cur的右兄弟结点
	}
	cout << t.tree[rt].data; //最终访问根结点
}

int main() {

}

树的括号表示法

【待补充】

森林的遍历【无代码演示】

森林有多颗树构成，每一棵树有一个根结点，可以定义一个辅助结点，森林中每颗子树的根结点作为其孩子结点，这样森林就变味一棵树，因此对森林的遍历可以转化为对树的遍历。

森林有如下两种遍历方法：
        先根遍历森林：从左到右依次先根遍历森林的各个子树。
        后根遍历森林：从左到右依次后根遍历森林的各个子树。

森林与二叉树的转换

森林树转换成二叉树后，对森林的操作都可以转换成对相应二叉树的操作。

森林转换成二叉树

 

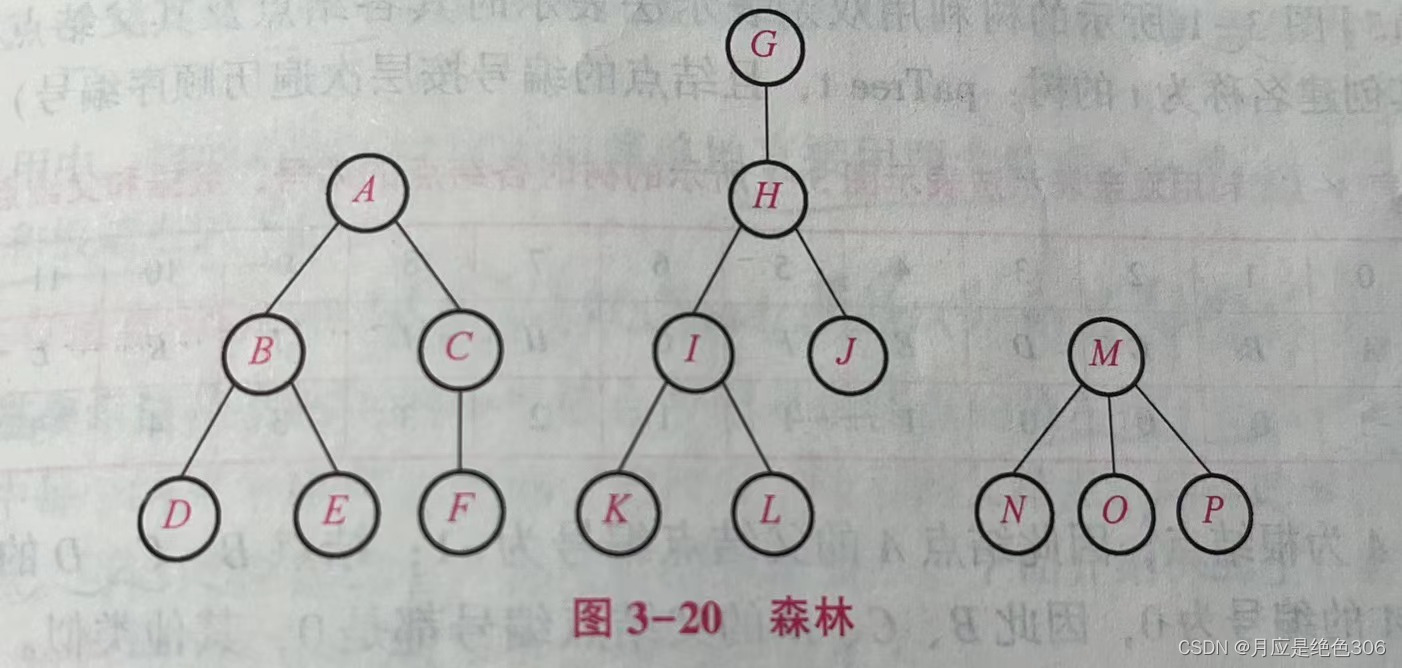
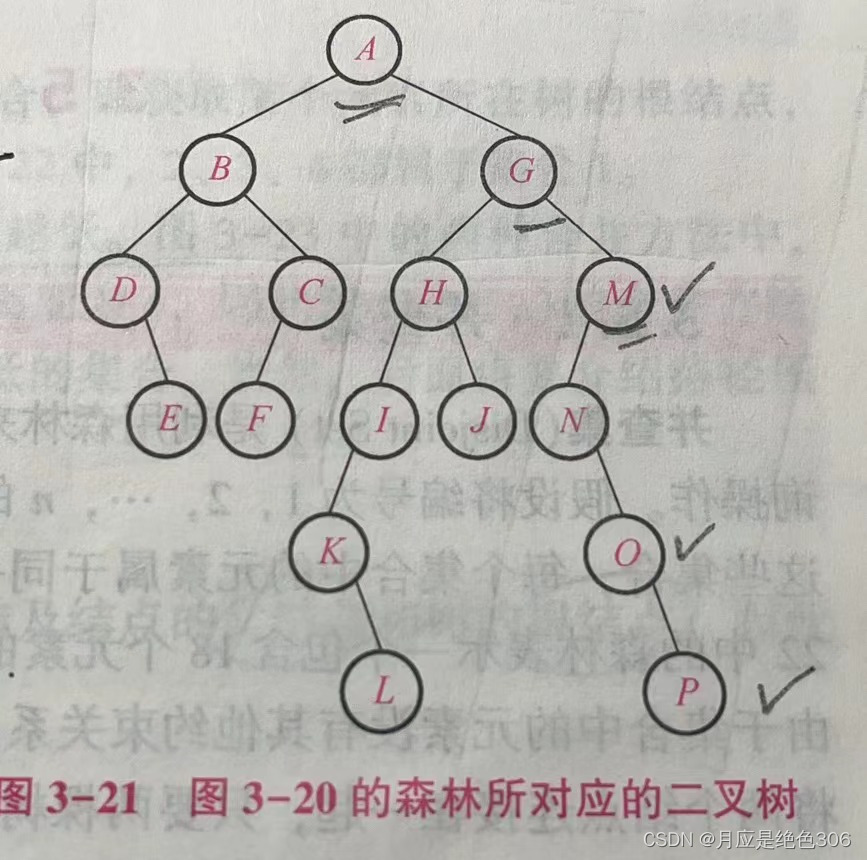
参考：

二叉树与树、森林之间的转换_kindoms214的博客-CSDN博客_将二叉树转换成对应的树或森林https://blog.csdn.net/kindoms214/article/details/85699598?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522167422309216800211583404%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=167422309216800211583404&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-85699598-null-null.142^v71^control_1,201^v4^add_ask&utm_term=%E4%BA%8C%E5%8F%89%E6%A0%91%E4%B8%8E%E6%A3%AE%E6%9E%97%E7%9A%84%E8%BD%AC%E6%8D%A2&spm=1018.2226.3001.4187