并查集
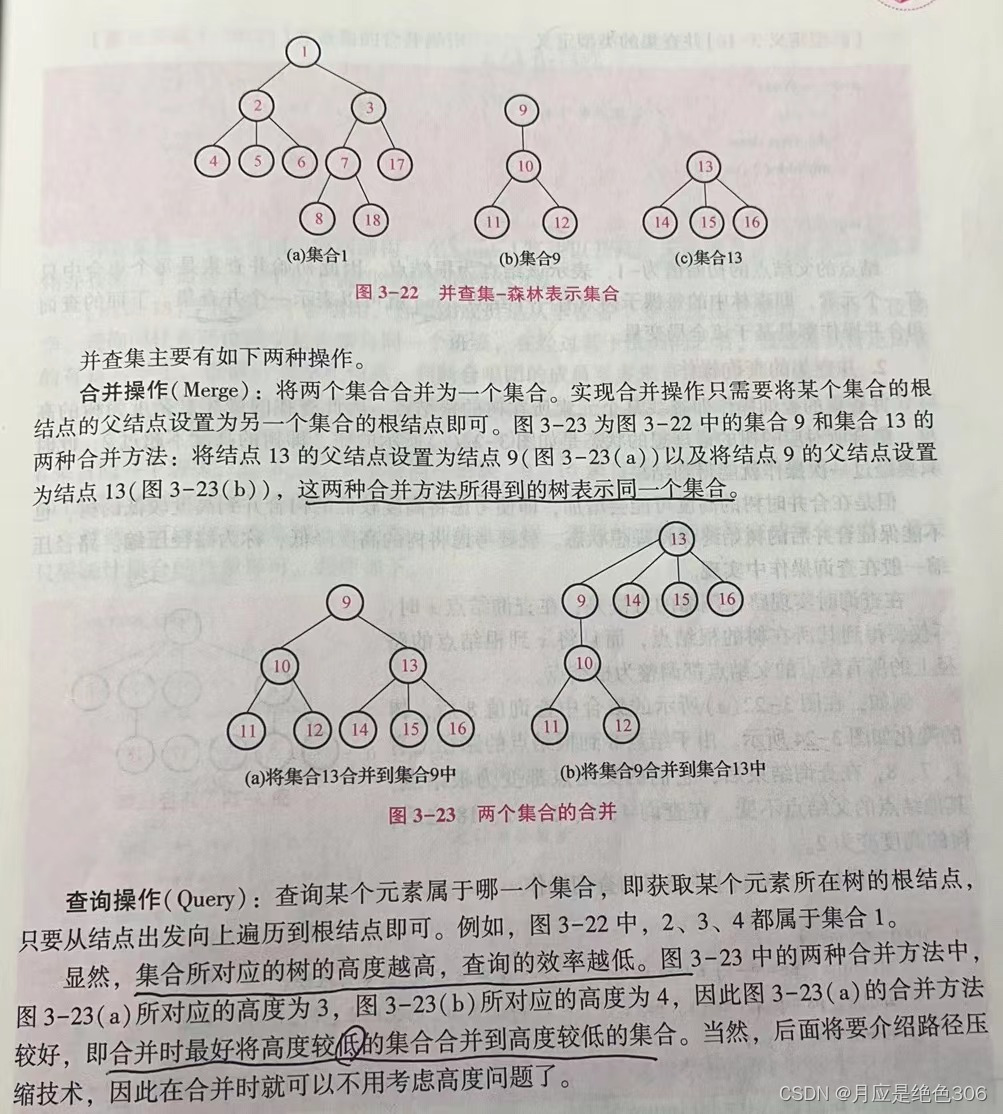
并查集是利用森林来描述一些不相交的集合,并支持集合的合并操作和查询操作。
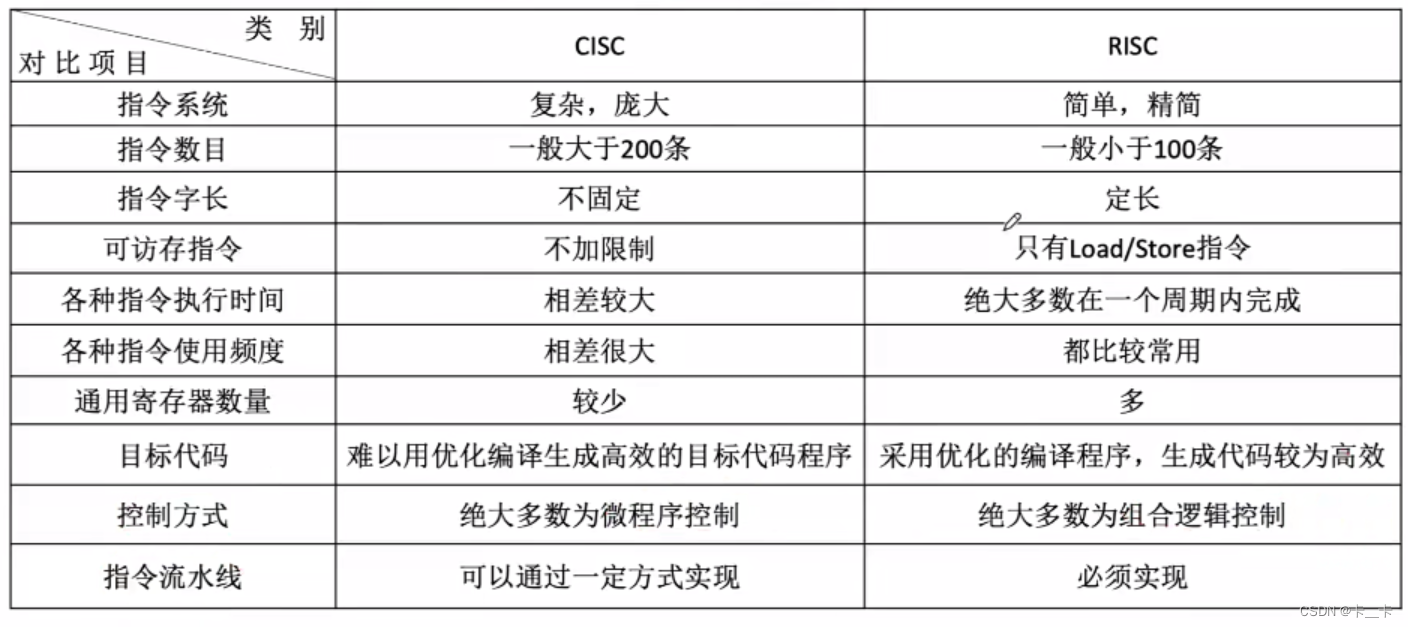
假设有n个元素,分为m个不相交集合,一个集合构成一棵树,同一棵树(集合)中的元素地位相等。例如下图的森林表示一个包含了18个元素的并查集,分为三个集合:集合1,9,13.
路径压缩:
在合并树的同时,考虑将树的高度也降低,一般运用于查询操作。
实现方法:
在查询结点x时,不仅要得到其所在树的根结点,而且将x到根结点的路径上的所有结点的父节点都调整为根结点。
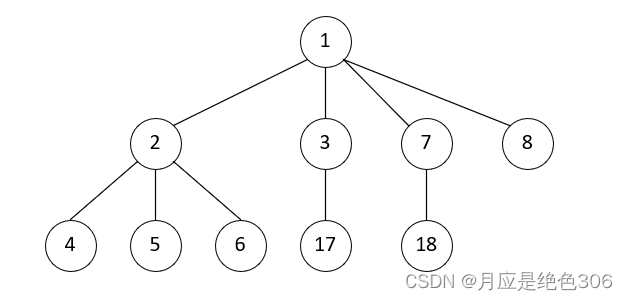
对图3-22(a)进行路径压缩,得到以下图
#include<iostream>
using namespace std;
typedef int datatype;
constexpr auto N = 100;
//由并查集的两种操作可知,并查集的操作中主要涉及结点的父节点和树的根结点,
//因此可以采用树的双亲表示法表示并查集。
//由下面并查集的类型定义可知,初始并查集每个集合里就一个元素,mq即表示一个并查集。
struct mqNode {
int pa;
datatype data;
mqNode() :pa(-1) {};
}mq[N];
//并查集的查询操作
int query(int x) {
if (mq[x].pa == -1)return x; //x没有父节点,则x为根结点
mq[x].pa = query(mq[x].pa); //向上查询x的父节点,并进行路径压缩,让x到根结点的路径都独立出来,成为第二层节点,链接根结点
return mq[x].pa;
}
//并查集的合并操作:1.获取两个元素所在树的根结点 2.检查两个元素是否属于同一集合
void merge(int x, int y) {
x = query(x), y = query(y);
if (x != y)
mq[x].pa = y;
}
int main() {
}并查集应用举例
并查集是一个很有用的数据结构,在Kruskal 算法以及判断无向图是否为连通图时都采用并查集。下面通过一个例子说明并查集的使用方法。
【例】 学校有一个合唱团,合唱团成员是从学校各个专业选拔上来的,共有n位同学。现询问任意两位同学是否来自同一个班级,在经过若干次询问之后,假设得到肯定回答的有m对学生。根据m 对学生信息,判断合唱团的成员至多来自多少个不同的班级。
例如,合唱团共有有10位成员,编号依次为1到10,设m=7,且7对同学分别为(1,2) , (2,6),(3,4),(8,5) , (5,4) , (9 10),(6,1)。则可以看出,1,2,6来自同一个班级,3、4、5、8来自同一班级,9、10来自同一班级,7没有信息,因此这10位同学至多来自4个班级。
显然,可以用并查集解决该问题,即将来自同一班级的两位同学所在的集合合并,最后
只要统计集合的数量即可。
void merge(int x, int y) {
x = query(x), y = query(y);
if (x != y)
mq[x].pa = y;
}
int num_class() {
int n, m, x, y, ret = 0;
cin >> n >> m;
for (int i = 0; i < m; i++) {
cin >> x >> y; //输入在同一班的两位学生编号
merge(x, y); //合并操作
}
for (int i = 0; i < n; i++) //统计集合数量
ret += mq[i].pa == -1;
return ret;
}树状数组